- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Равенство треугольников
Содержание
- 2. ТреугольникТреугольник - простейшая плоская фигура. Три вершины
- 3. Первое упоминание о треугольнике и его свойствах
- 4. Виды треугольников
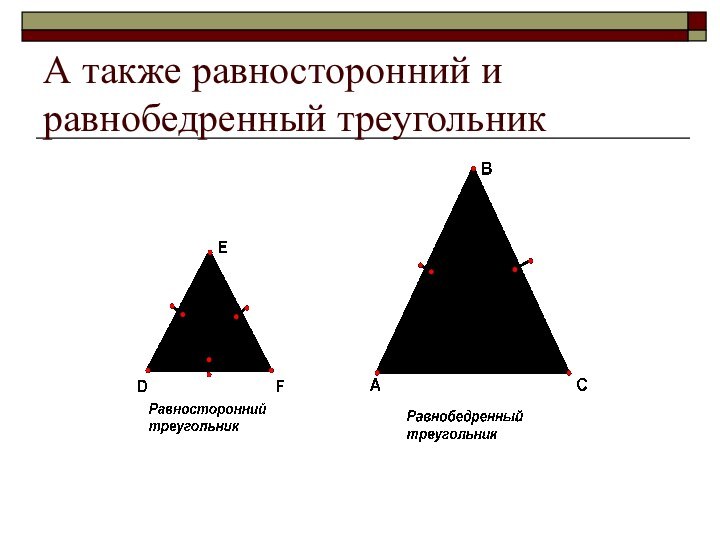
- 5. А также равносторонний и равнобедренный треугольник
- 6. Медиана треугольникаОтрезок соединяющий вершину треугольника с серединой
- 7. Высота треугольникаПерпендикуляр проведенный из вершины треугольника к
- 8. Биссектриса треугольникаОтрезок биссектрисы угла треугольника, соединяющий вершину
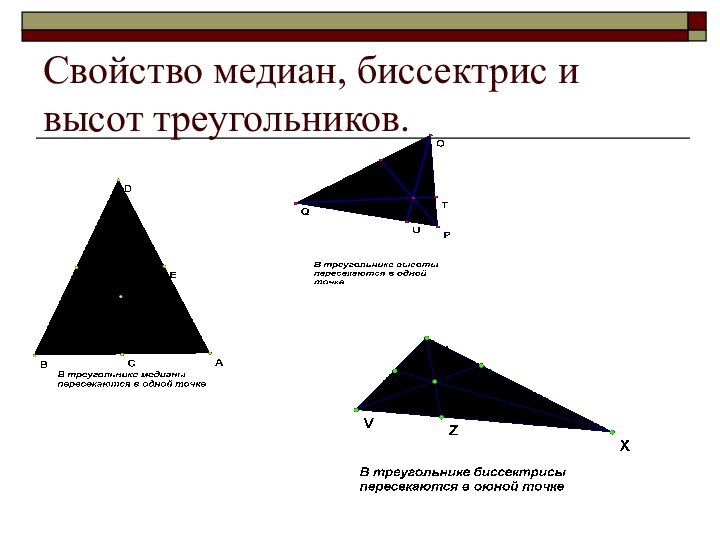
- 9. Свойство медиан, биссектрис и высот треугольников.
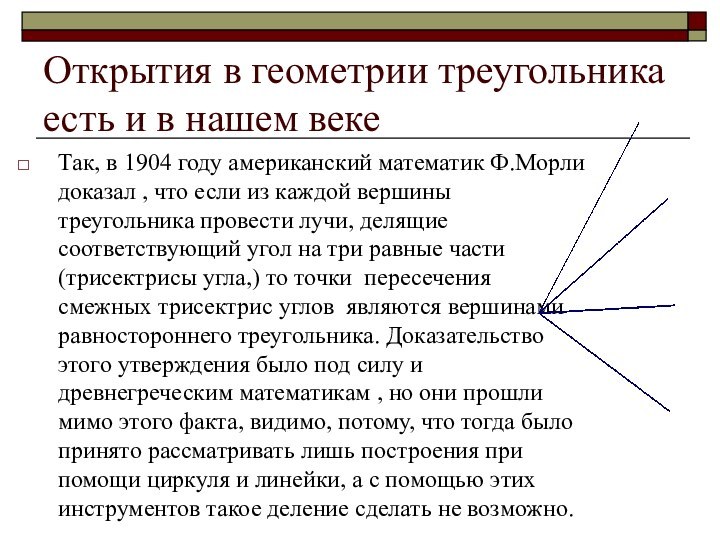
- 10. Открытия в геометрии треугольника есть и в
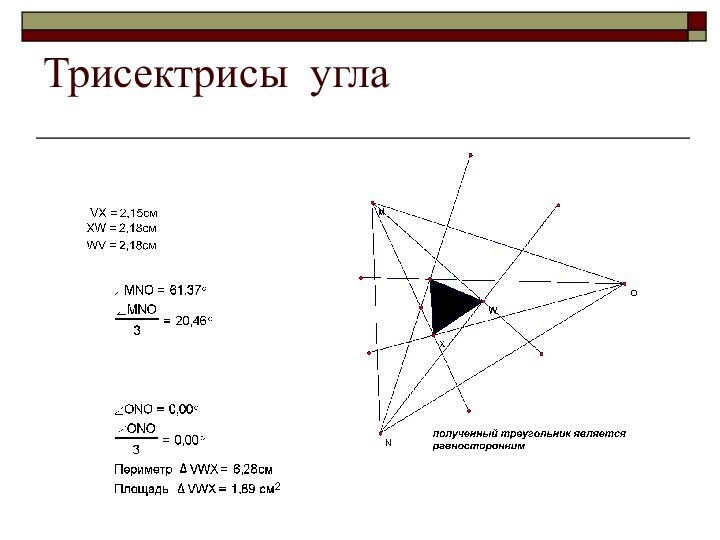
- 11. Трисектрисы угла
- 12. А вот и сами три признака 1
- 13. 2-й признакЕсли сторона и два прилежащих угла
- 14. 3-й признакЕсли три стороны одного треугольника соответственно
- 15. Скачать презентацию
- 16. Похожие презентации
ТреугольникТреугольник - простейшая плоская фигура. Три вершины и три стороны. Изучение треугольника породило науку – тригонометрию. Эта наука возникла из практических потребностей при измерении земельных участков, составлении карт на местности, конструировании машин и механизмов.