- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора в занимательных задачах
Содержание
- 2. Цель урока Обобщение и расширение знаний учащихся по данной теме.
- 3. Задачи урока:учебно-познавательная: формирование умений применять теорему Пифагора
- 4. Что вы знаете об этом ученом?
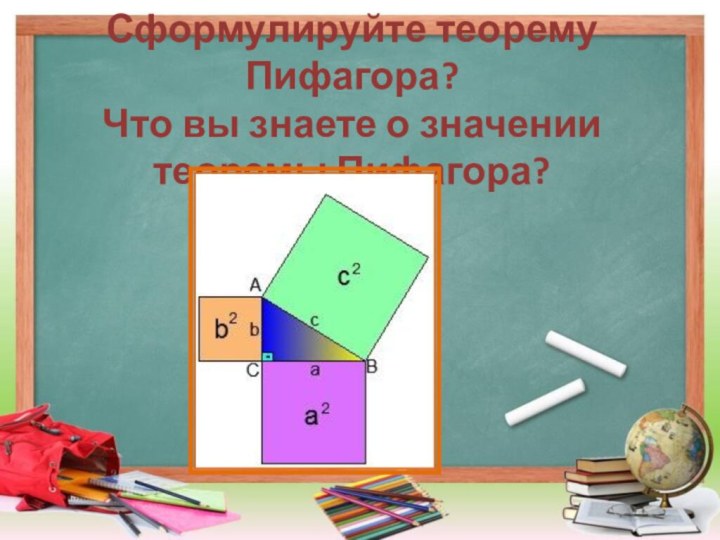
- 5. Сформулируйте теорему Пифагора? Что вы знаете о значении теоремы Пифагора?
- 6. Доказательство теоремы считалось в кругах учащихся средних
- 7. Карикатуры
- 8. СтишкиПифагоровы штаны на все стороны равны…Если дан
- 9. Египетский треугольникПоговорим о треугольнике со сторонами 3;
- 10. Правило веревки “Правило веревки” использовалось для построения алтарей,
- 11. Задача индийского математика Бхаскары«На берегу реки рос
- 12. Древнеиндейская задачаНад озером тихим, С полфута размером,
- 13. ACDBДано: DCB,
- 14. Задача кассиршиТри монеты лежат на столе, касаясь
- 15. Путь жукаУ дороги лежит тесанный гранитный камень
- 16. Решение Кратчайший путь легко определить, если мы
- 17. Из «Арифметики» МагницкогоСлучися некоему человеку к стене
- 18. Решение
- 19. Арабская задачаНа разных берегах реки растет по
- 20. Домашнее задание Подобрать занимательные, исторические, межпредметные задачи, в решении которых применяется теорема Пифагора.
- 21. Спасибо за урок
- 22. Скачать презентацию
- 23. Похожие презентации
Цель урока Обобщение и расширение знаний учащихся по данной теме.
Слайд 3
Задачи урока:
учебно-познавательная: формирование умений применять теорему Пифагора в
стандартных и не стандартных ситуациях;
развивающая: сформировать представление у учащихся
о межпредметных связях.Слайд 6 Доказательство теоремы считалось в кругах учащихся средних веков
очень трудным и называлось:
“Dons asinorum” -
«ослиный мост»
или
“elefuga”
-«бегство убогих»
«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
а сама теорема –
Слайд 8
Стишки
Пифагоровы штаны на все стороны равны…
Если дан нам
треугольник И притом с прямым углом, То квадрат гипотенузы
Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим — И таким простым путем К результату мы придем.
Слайд 9
Египетский треугольник
Поговорим о треугольнике со сторонами 3; 4
и 5. За 1500 лет до Пифагора древние египтяне
знали о том, что треугольник со сторонами 3, 4, 5 является прямоугольным, и пользовались этим свойством (т.е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.5
4
3
Слайд 10
Правило веревки
“Правило веревки” использовалось для построения алтарей, которые
по священному предписанию должны были иметь строгую геометрическую ориентацию
относительно четырех сторон горизонта, а так же при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике.ЗАДАНИЕ: Показать веревку с завязанными на ней узлами и показать как получается прямой угол.
Слайд 11
Задача индийского математика Бхаскары
«На берегу реки рос тополь
одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. Угол
прямойС теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Оказалось три фута всего от ствола.
Прошу тебя, мне поскорее скажи:
У тополя как велика высоты?»
1150 г.
Слайд 12
Древнеиндейская задача
Над озером тихим,
С полфута размером, высился лотоса
цвет. Он рос одиноко. И ветер порывом Отнес его в сторону.
Нет Боле цветка над водой. Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода здесь глубока?(Перевод В.И.Лебедева)
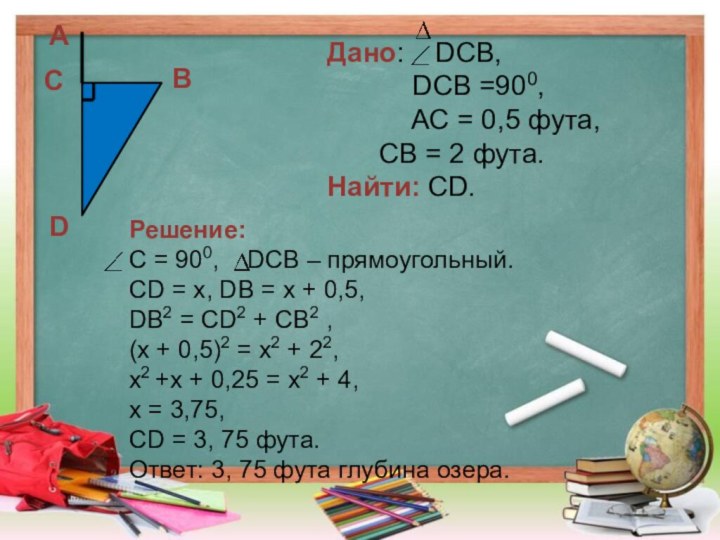
Слайд 13
A
C
D
B
Дано: DCB,
DCB =900,
AC =
0,5 фута,CB = 2 фута.
Найти: CD.
Решение:
C = 900, DCB – прямоугольный.
CD = x, DB = x + 0,5,
DB2 = CD2 + CB2 ,
(x + 0,5)2 = x2 + 22,
x2 +x + 0,25 = x2 + 4,
x = 3,75,
CD = 3, 75 фута.
Ответ: 3, 75 фута глубина озера.
Слайд 14
Задача кассирши
Три монеты лежат на столе, касаясь друг
друга, а их центры образуют прямоугольный треугольник. Приведите их
размеры, выраженные наименьшими возможными целыми числами.
Слайд 15
Путь жука
У дороги лежит тесанный гранитный камень в
30 см длины, 20 см высоты и такой же
толщины. В точке А – жук, намеревающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?
Слайд 16
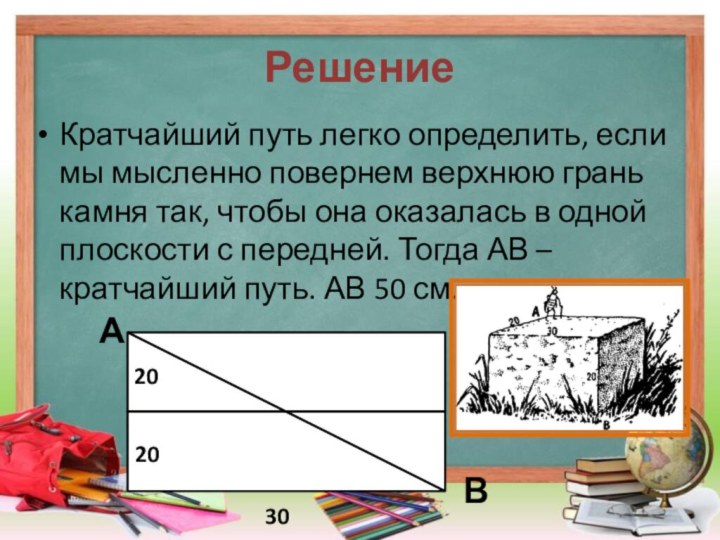
Решение
Кратчайший путь легко определить, если мы мысленно
повернем верхнюю грань камня так, чтобы она оказалась в
одной плоскости с передней. Тогда АВ – кратчайший путь. АВ 50 см.А
В
20
20
30
Слайд 17
Из «Арифметики» Магницкого
Случися некоему человеку к стене лествицу
прибрати, стены же тоя высота есть 117 стоп. И
обретя лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.
Слайд 19
Арабская задача
На разных берегах реки растет по пальме.
Высота одной – 30 локтей, а другой 20, а
расстояние между основаниями пальм – 50 локтей. На верхушке каждой пальмы сидит птица. Обе птицы заметили рыбу, всплывающую на поверхность реки между пальмами. Птицы кинулись разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы всплыла раба?
Слайд 20
Домашнее задание
Подобрать занимательные, исторические, межпредметные задачи, в
