Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Сферическая поверхность. Шар 11 класс

Содержание

СодержаниеСферическая поверхностьУравнение сферыВзаимное расположение сферы и плоскости Касательная плоскость к сфереПлощадь сферы, объем шараВопросы
Сферическая поверхность. ШарГеометрия 11 классР.О.Калошина, ГОУ лицей №533Санкт-Петербург СодержаниеСферическая поверхностьУравнение сферыВзаимное расположение сферы и плоскости Касательная плоскость к сфереПлощадь сферы, объем шараВопросы Сферическая поверхностьСферической поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки Сферическая поверхность (продолжение)O – центр сферыR – радиус сферыОсь – любая прямая, проходящая через центр сферы Уравнение сферыВ прямоугольной системе координат уравнение сферы радиуса R с центром Взаимное расположение сферы и плоскостиЕсли расстояние от центра сферы до плоскости меньше Взаимное расположение сферы и плоскости (продолжение)Если расстояние от центра сферы до плоскости Взаимное расположение сферы и плоскости (окончание)Если расстояние от центра сферы до плоскости 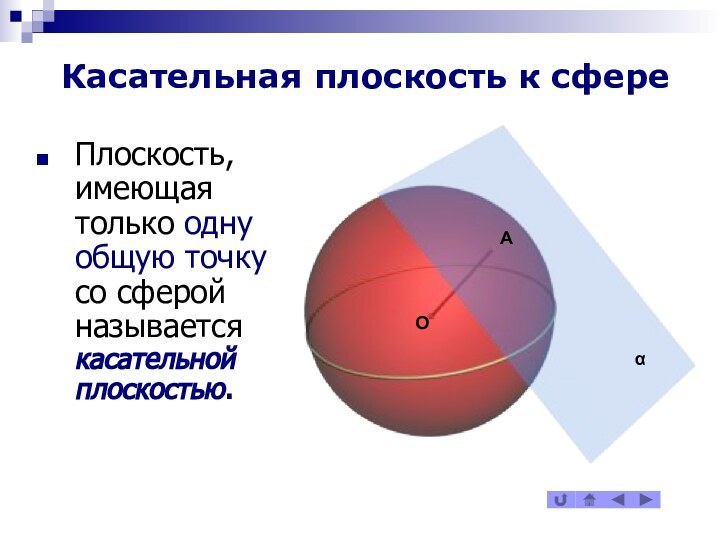Касательная плоскость к сфереПлоскость, имеющая только одну общую точку со сферой называется касательной плоскостью. Касательная плоскость к сфере (продолжение)Теорема: Радиус сферы, проведенный в точку касания сферы Площадь сферы, объем шара (продолжение)Теорема АрхимедаОбъем шара в полтора раза меньше объема Площадь сферы, объем шараПлощадь поверхности шара радиуса R равна учетверенной площади большого Вопросы для закрепленияДайте определение сферы, шара.Можно ли рассматривать сферу как поверхность вращения,
Слайды презентации

Слайд 2 Содержание
Сферическая поверхность
Уравнение сферы
Взаимное расположение сферы и плоскости
Касательная

СодержаниеСферическая поверхностьУравнение сферыВзаимное расположение сферы и плоскости Касательная плоскость к сфереПлощадь сферы, объем шараВопросы

плоскость к сфере
Площадь сферы, объем шара
Вопросы


Слайд 3 Сферическая поверхность
Сферической поверхностью называется геометрическое место точек пространства,

Сферическая поверхностьСферической поверхностью называется геометрическое место точек пространства, равноудаленных от одной

равноудаленных от одной точки – центра.

Тело, ограниченное сферической поверхностью,

называется шаром.





Слайд 4 Сферическая поверхность (продолжение)
O – центр сферы
R – радиус сферы
Ось

Сферическая поверхность (продолжение)O – центр сферыR – радиус сферыОсь – любая прямая, проходящая через центр сферы

– любая прямая, проходящая через центр сферы




Слайд 5 Уравнение сферы
В прямоугольной системе координат уравнение сферы радиуса

Уравнение сферыВ прямоугольной системе координат уравнение сферы радиуса R с центром C (xo;yo;zo) имеет вид: (x-xo)²+(y-yo)²+(z-zo)²=R²

R с центром C (xo;yo;zo) имеет вид:
(x-xo)²+(y-yo)²+(z-zo)²=R²




Слайд 6 Взаимное расположение сферы и плоскости
Если расстояние от центра

Взаимное расположение сферы и плоскостиЕсли расстояние от центра сферы до плоскости

сферы до плоскости меньше радиуса сферы, то сечение сферы

плоскостью есть окружность:
d





Слайд 7 Взаимное расположение сферы и плоскости (продолжение)
Если расстояние от

Взаимное расположение сферы и плоскости (продолжение)Если расстояние от центра сферы до

центра сферы до плоскости равно радиусу сферы, то сфера

и плоскость имеют только одну общую точку (точку касания)





Слайд 8 Взаимное расположение сферы и плоскости (окончание)
Если расстояние от

Взаимное расположение сферы и плоскости (окончание)Если расстояние от центра сферы до

центра сферы до плоскости больше радиуса сферы, то сфера

и плоскость не имеют общих точек





Слайд 9 Касательная плоскость к сфере
Плоскость, имеющая только одну общую

Касательная плоскость к сфереПлоскость, имеющая только одну общую точку со сферой называется касательной плоскостью.

точку со сферой называется касательной плоскостью.




Слайд 10 Касательная плоскость к сфере (продолжение)




Теорема: Радиус сферы, проведенный

Касательная плоскость к сфере (продолжение)Теорема: Радиус сферы, проведенный в точку касания

в точку касания сферы и плоскости, перпендикулярен к касательной

плоскости.

Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Слайд 11 Площадь сферы, объем шара (продолжение)
Теорема Архимеда
Объем шара в полтора

Площадь сферы, объем шара (продолжение)Теорема АрхимедаОбъем шара в полтора раза меньше

раза меньше объема описанного вокруг него цилиндра, а площадь

поверхности шара в полтора раза меньше площади полной поверхности того же цилиндра:

V= (2/3)V1 S= (2/3)S1
где V1 – объем описанного цилиндра, S1 – площадь полной поверхности этого цилиндра





Слайд 12 Площадь сферы, объем шара
Площадь поверхности шара радиуса R

Площадь сферы, объем шараПлощадь поверхности шара радиуса R равна учетверенной площади

равна учетверенной площади большого круга: S=4πR²

Объем шара радиуса R

равен V = (4/3)πR³





  • Имя файла: sfericheskaya-poverhnost-shar-11-klass.pptx
  • Количество просмотров: 134
  • Количество скачиваний: 0
- Предыдущая Внедрение стандартов ISO на примере компании Kraft
Следующая - Architektur in Deutschland.

Похожие презентации

Окружность и круг (5 класс) Окружность и круг (5 класс) 218
Презентация по математике на тему Египетский треугольник (8 класс) Презентация по математике на тему Египетский треугольник (8 класс) 210
Презентация 3 Провешивание прямой на местности по геометрии 7 класс Презентация 3 Провешивание прямой на местности по геометрии 7 класс 169
Тригонометрические уравнения Тригонометрические уравнения 190
Удивительный квадрат (8 класс) Удивительный квадрат (8 класс) 147
Таблицы по геометрии Таблицы по геометрии 184
Определение параболы Определение параболы 175
Объемы тел Объемы тел 174
Следствия Следствия 139
История теоремы Пифагора История теоремы Пифагора 158
Первый признак равенства треугольников Первый признак равенства треугольников 169
Как определить длину окружности Как определить длину окружности 188
Геометрия на вольном воздухе Геометрия на вольном воздухе 151
Музыка Музыка 178
Смежные и вертикальные углы Смежные и вертикальные углы 150
Определение вектора в пространстве Определение вектора в пространстве 193
Задачи на подобие треугольников Задачи на подобие треугольников 194
Презентация по геометрии 8 кл на тему: Применение подобия треугольников к решению задач Презентация по геометрии 8 кл на тему: Применение подобия треугольников к решению задач 185
Презентация по геометрии на тему Правильные многогранники Презентация по геометрии на тему Правильные многогранники 184
Презентация по геометрии на тему Прямые и плоскости в пространстве 10 класс Презентация по геометрии на тему Прямые и плоскости в пространстве 10 класс 848
Симметрия в жизни Симметрия в жизни 174
Угол. Прямой и развернутый угол Угол. Прямой и развернутый угол 142
Параллельные прямые Параллельные прямые 172
Куля Куля 168
Презентация по геометрии на тему Площадь параллелограмма (8 класс) Презентация по геометрии на тему Площадь параллелограмма (8 класс) 170
Презентация к уроку геометрии в 8 классе по теме Четырёхугольники Презентация к уроку геометрии в 8 классе по теме Четырёхугольники 137
Липецк купеческий подготовка к ОГЭ интегрированный урок геометрия, искусство и краеведение для учащихся 8 класса Липецк купеческий подготовка к ОГЭ интегрированный урок геометрия, искусство и краеведение для учащихся 8 класса 147
Презентация по геометрии на тему Скрещивающиеся прямые (10 класс) Презентация по геометрии на тему Скрещивающиеся прямые (10 класс) 160
Презентация Свойства равнобедренного треугольника Презентация Свойства равнобедренного треугольника 144
Следствия из аксиом стереометрии Следствия из аксиом стереометрии 168