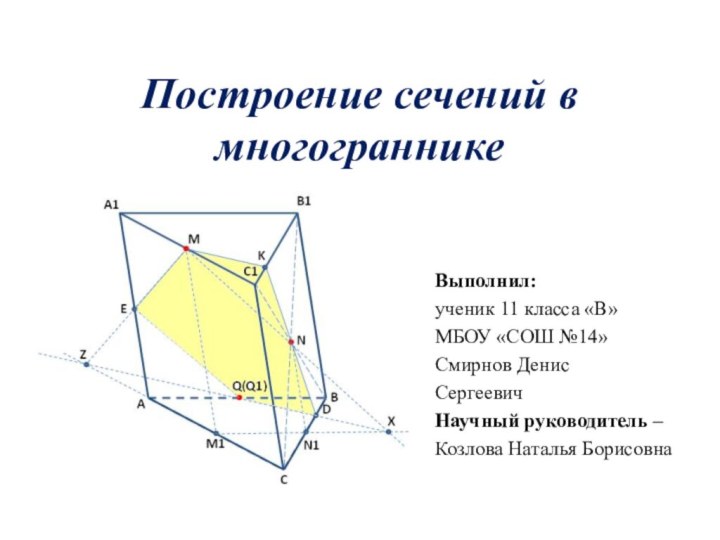
Слайд 2
Цель работы: исследование методов построения сечений многогранников.
В
связи с поставленной целью, необходимо было решить ряд задач:
Изучение
литературы по теме; обобщить, систематизировать данный материал;
Рассмотреть и исследовать различные способы построения сечений в стереометрии;
Классифицировать задачи с учетом задания точек сечения и методом построения сечения.
Составить алгоритм построения сечений;
Изучить способы проверки правильности построенного сечения;
Оценить результат проделанной работы.
Слайд 3
Объект исследования – методы построения сечений многогранников,
Предмет
исследования – задачи на построение сечений многогранников.
Методы исследования:
- обзор литературы по теме;
- анализ различных способов построений, применяемых к задачам;
- анкетирование одноклассников;
- построение сечения своего многогранника(эксперимент»).
Слайд 4
Практическая значимость данного материала
Уровень производства, научно-технический прогресс предъявляют
к современному специалисту среднего звена высокие требования. Для специалиста
– техника важно составлять грамотно техническую документацию, а для этого нужны знания. Решая задачи на построение секущих плоскостей на различных геометрических телах, мы учимся определять линии пересечения плоскостей, что несомненно пригодится при построении чертежей разрезов деталей.
Слайд 5
Методы построения сечений
Аксиоматический метод.
Метод внутреннего проектирования
Комбинированный метод.
Слайд 6
Суть метода заключается в построении вспомогательной прямой, являющейся
изображением линии пересечения секущей плоскости с плоскостью какой-либо грани
фигуры F . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани Построение сечения многогранника методом следов обычно начинают с построения, так называемого, основного следа секущей плоскости, т. е. следа секущей плоскости на плоскость основания многогранника.
распечатаем
Слайд 7
Аксиоматический метод построения сечений
Метод следа
Суть метода заключается в
построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости
с плоскостью какой-либо грани фигуры F Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани.
Слайд 8
Аксиоматический метод построения сечений
Метод внутреннего проектирования
Этот метод удобен
при построении сечений в тех случаях, когда почему-либо неудобно
находить след секущей плоскости, например, след получается очень далеко от заданной фигуры
Слайд 9
Аксиоматический метод построения сечений
Комбинированный метод
Комбинированный метод построения сечений
многогранников заключается в том, что при построении этим методом
на каких-то этапах построения сечения применяются приёмы метода следа, а на каких-то применяются теоремы о параллельности прямых и плоскостей в пространстве.
Слайд 10
Правила построения сечений методом следа
Если даны (или уже
построены) две точки плоскости сечения на одной грани многогранника,
то след сечения этой плоскости – прямая, проходящая через эти точки.
Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определённой боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью (точка пересечения данного следа с общей прямой основания и данной боковой грани)
Точку пересечения плоскости сечения с основанием можно определить, как точку пересечения какой-либо прямой в плоскости сечения с её проекцией на плоскость основания.
Слайд 11
Алгоритм построения сечений
1) Определить вид данной фигуры .
2)
Проанализировать данные:
Если даны 3 точки, то где они находятся.
Есть
ли пара точек, лежащих в одной грани.
Лежит ли третья точка в плоскости какой-то грани или в её продолжении, а может она лежит в пространстве.
Если даны точка и прямая линия или две прямые, то где они находятся, что я знаю о них.
Если нет по условию двух точек, лежащих в плоскости одной грани многогранника или одна из трёх точек находится внутри фигуры или же снаружи, находясь в пространстве, то поступать надо так:
Сначала надо построить вспомогательную плоскость, которая пересекала бы основание данной фигуры или его продолжение, которая в свою очередь будет пересекать какие-то стороны основания или их продолжение.
Слайд 12
Проверка правильности построенного сечения
Построенное сечение выпуклого многогранника всегда
выпуклый многоугольник.
Вершины сечения всегда лежат на соответствующих рёбрах данного
многогранника.
Точки, лежащие на гранях многогранника, обязательно должны лежать на сторонах многоугольника, полученного в сечении.
Две стороны многоугольника, получившегося в сечении, не могут принадлежать одной грани данного многогранника.
Если сечение пересекает параллельные грани у многогранника, то и соответствующие этим граням стороны построенного сечения должны быть параллельны.
Слайд 13
Примеры построения сечений
в многогранниках
Слайд 14
Задача №1
Построить сечение пирамиды NABCD плоскостью, проходящей через
точку М, принадлежащую ребру NB, точку Р, принадлежащую
ребру NA и точку К, принадлежащую плоскости, на которой стоит пирамида.
P и M (NAB), значит след секущей плоскости проходит по (PM)
(PM) (AB) = F α
К α, то след секущей плоскости проходит по (FK)
(FK) (AD) = E,
(FK) (DC) = R
След - ER
(FK) (BC) = T
(MT) (NС) = Q
Т. к. P и Е (AND), то проводим (PE)
(PMQRE) - искомое сечение.
Слайд 15
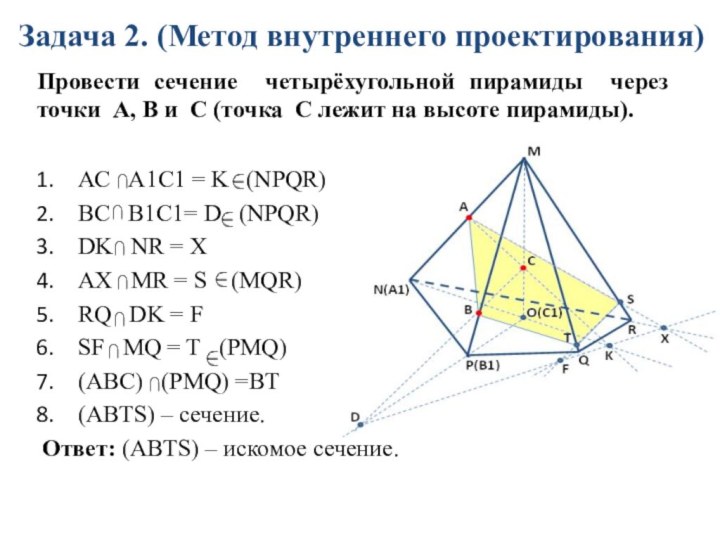
Задача 2. (Метод внутреннего проектирования)
Провести сечение четырёхугольной пирамиды
через точки A, В и C (точка С лежит
на высоте пирамиды).
АС А1С1 = K (NPQR)
BC B1C1= D (NPQR)
DK NR = Х
AХ MR = S (MQR)
RQ DK = F
SF MQ = T (PMQ)
(ABC) (PMQ) =BT
(ABTS) – сечение.
Ответ: (ABTS) – искомое сечение.
Слайд 16
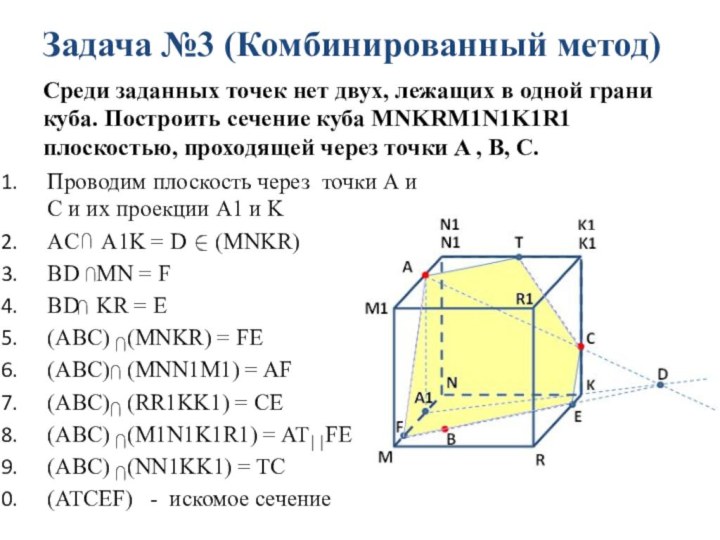
Задача №3 (Комбинированный метод)
Среди заданных точек нет двух,
лежащих в одной грани куба. Построить сечение куба МNKRM1N1K1R1
плоскостью, проходящей через точки A , B, C.
Проводим плоскость через точки А и С и их проекции А1 и K
AC A1K = D (МNKR)
BD MN = F
BD KR = E
(ABC) (МNKR) = FE
(ABC) (MNN1M1) = AF
(ABC) (RR1KK1) = CE
(ABC) (M1N1K1R1) = AT FE
(ABC) (NN1KK1) = TC
(ATCEF) - искомое сечение
Слайд 17
Сечения в задачах ЕГЭ
(Задание №14)
Слайд 18
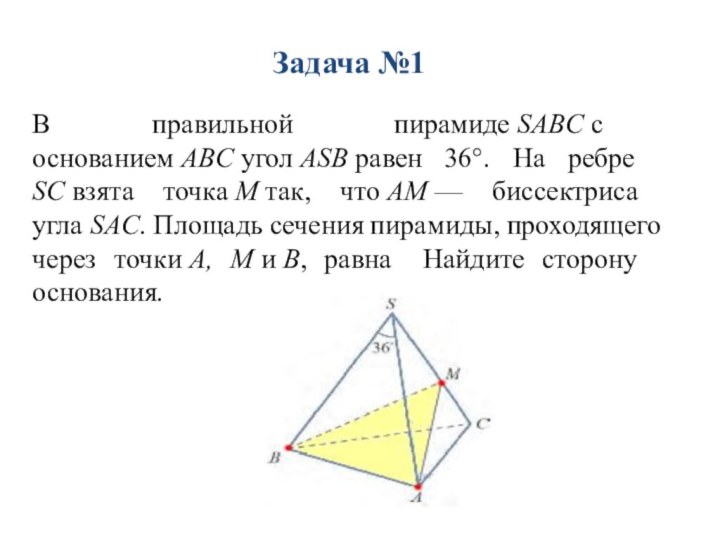
Задача №1
В правильной пирамиде SABC с
основанием ABC угол ASB равен 36°. На ребре SC взята точка M так, что AM — биссектриса угла SAC. Площадь сечения пирамиды, проходящего через точки A, M и B, равна Найдите сторону основания.
Слайд 20
Задача №2
В правильной четырехугольной пирамиде PABCD, все ребра которой
равны 4, точка K ― середина бокового ребра AP. а)
Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Слайд 22
Задача № 3
Точка Е — середина ребра CC1
куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью A1BE если
ребра куба равны 2.
Слайд 24
Построение сечения сложного многогранника (комбинированный метод).
Прямоугольный параллелепипед стоит
на кубе так, что противоположные боковые грани параллелепипеда и
куба соответственно параллельны. Требуется построить в образовавшемся теле сечение, проходящее через точки M, N, P.
Слайд 26
Анкетирование одноклассников
Из проведённой мною анкеты видно, что тема
«Построение сечений многогранников» необходима, для того, чтобы знать внутреннюю
структуру предмета, кроме того ребят заинтересовал вопрос об использовании многогранников( ведь все семь чудес света построены на основе многогранников). Хотелось бы ещё отметить тот факт, что одноклассники забыли факты, определяющие секущую плоскость.
Слайд 27
Заключение
Проведя исследование построения сечения методом следов, я установил,
что метод следов легко объясним, нагляден, но не всегда
удобен в практике построения сечений многогранников, так как расположение точек Х и У следа s может быть за рамками чертежа, прямые, определяющие точку Х (или Y) могут быть параллельны. В тех случаях, когда применение метода следа затруднено, применяют метод внутреннего проецирования или так называемый метод вспомогательных сечений или комбинированный метод.
Знание методов построения сечений, способов нахождения точек и линий пересечения секущих плоскостей с различными геометрическими объектами поможет в будущем и при изучении общепрофессиональных дисциплин, и при работе инженера, что очень важно для любого конкурентоспособного специалиста, что бы выяснить внутреннее строение предмета.