Презентация на тему Скалярное произведение векторов

аналогичные свойствам произведения чисел:

1.

2.

3.









Используя формулу

между векторами:
а) и

Ответ: а) 90о;

б) 135о;

в) 90о;

г) 120о;

д) 135о.

Найдите скалярное произведение векторов:
а)

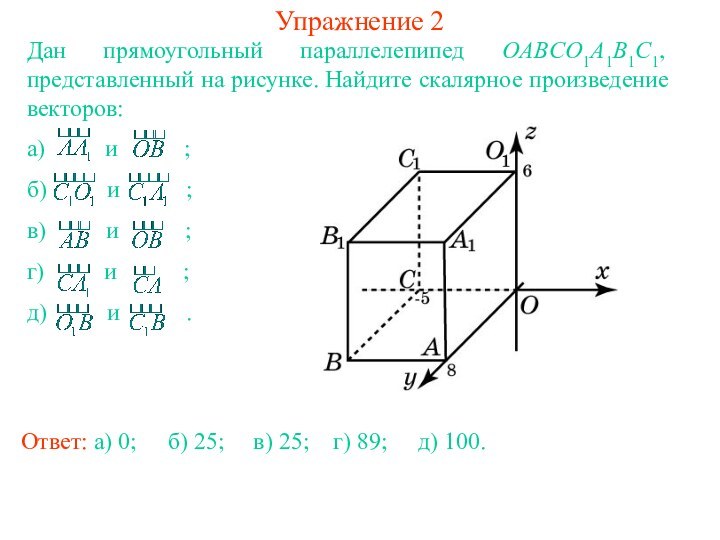
Ответ: а) 0;

б) 25;

в) 25;

г) 89;

д) 100.

и (2,-1,0).

Ответ: –4.

угол между ними: а) острый; б) тупой?
Ответ: а) Плюс;

б) минус.

векторов равно нулю?
Ответ: Если они перпендикулярны.

и (1,-2,4);

б) (1,2,-2)

б) ϕ = 45о.

Ответ: z = -2.

AB, AD, DC правильного тетраэдра с ребром 4. Найдите

Ответ: а) 2;

б) -2;

в) -2;

г) 1;

д) -1;

е) 0.

вектор:
а)
б)
в)
г) (0,3,4).








в) 180о, 90о, 90о;