Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Билеты устного экзамена по геометрии

Содержание

Прямоугольный треугольник Треугольник, у которого один из углов прямой, называется прямоугольным. ∆ACB – прямоугольный
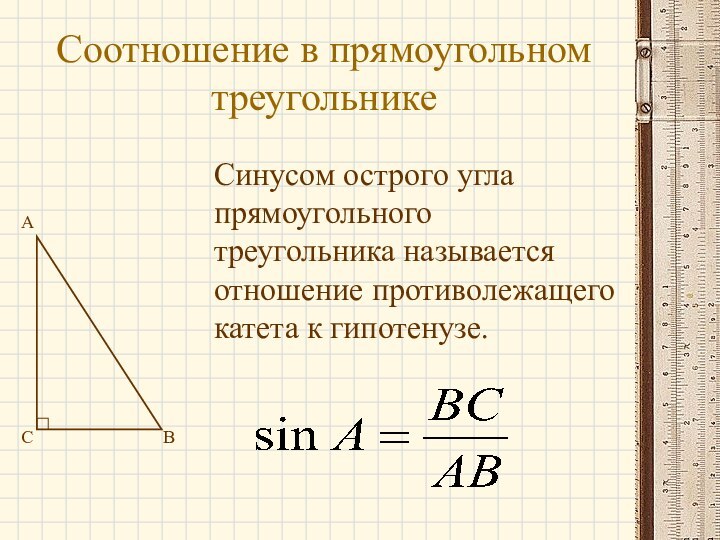
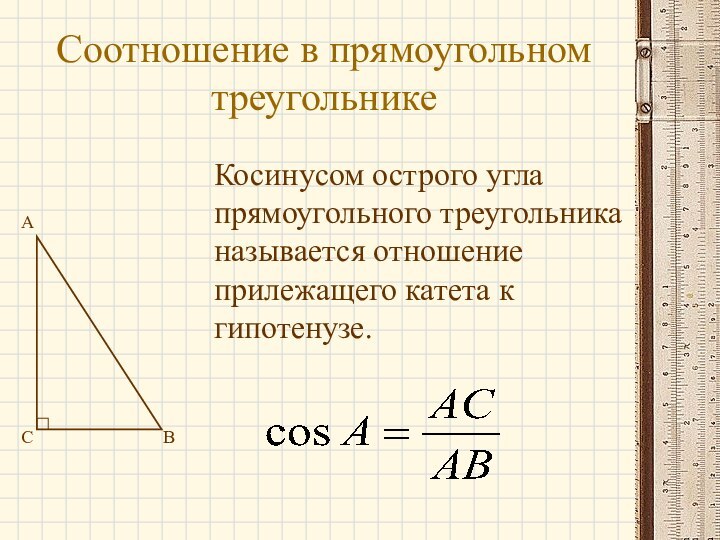
9 класс Билеты устного экзамена по геометрии Билет №8 Прямоугольный треугольник Треугольник, у которого один из углов прямой, называется прямоугольным. ∆ACB – прямоугольный Соотношение в прямоугольном треугольникеABCСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Соотношение в прямоугольном треугольникеABCКосинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 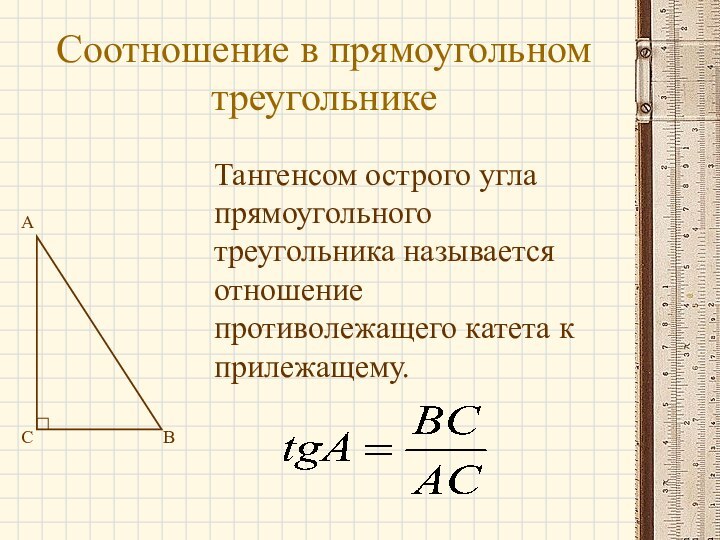Соотношение в прямоугольном треугольникеABCТангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. 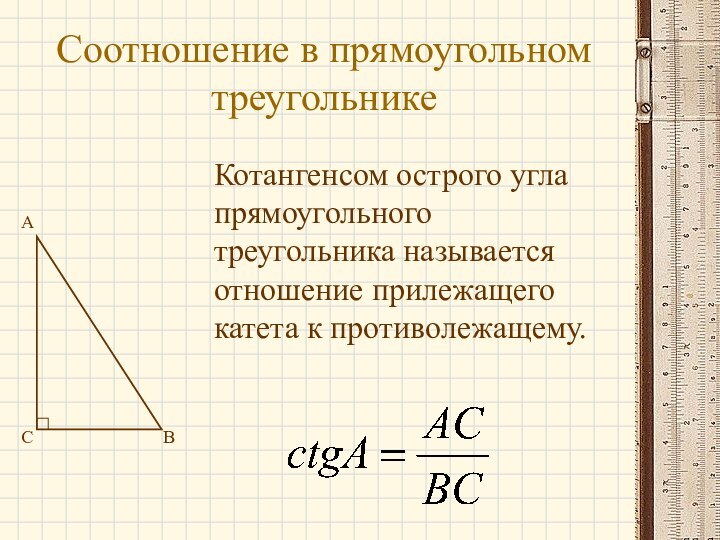Соотношение в прямоугольном треугольникеABCКотангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему. 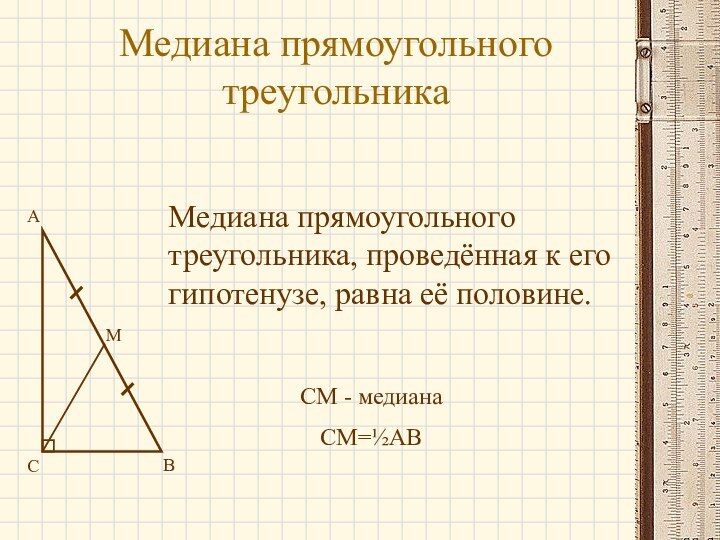Теорема Пифагора Теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2ABCcab Теорема Пифагора Доказательство Дано: ∆ACB – прямоугольный Доказать: c2 = a2 + b2 Доказательство:BCcabAbbbaaacccДостроим ∆ACB до Соотношения в прямоугольном треугольникеАСBbcaacbchABC – прямоугольный треугольникCH - высотаh2 = acbc h = Медиана прямоугольного треугольника Медиана прямоугольного треугольника, проведённая к его гипотенузе, равна её половине.СABMCM - медианаCM=½AB Медиана прямоугольного треугольника ДоказательствоДано: ∆ACB – прямоугольныйСМ – медианаДоказать: CM=½ABДоказательство:СABM1) Построим
Слайды презентации

Слайд 2 Прямоугольный треугольник
Треугольник, у которого один из углов

Прямоугольный треугольник Треугольник, у которого один из углов прямой, называется прямоугольным. ∆ACB – прямоугольный

прямой, называется прямоугольным.

∆ACB – прямоугольный

Слайд 3 Соотношение в прямоугольном треугольнике


A
B
C
Синусом острого угла прямоугольного треугольника

Соотношение в прямоугольном треугольникеABCСинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

называется отношение противолежащего катета к гипотенузе.


Слайд 4 Соотношение в прямоугольном треугольнике


A
B
C
Косинусом острого угла прямоугольного треугольника

Соотношение в прямоугольном треугольникеABCКосинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

называется отношение прилежащего катета к гипотенузе.

Слайд 5 Соотношение в прямоугольном треугольнике


A
B
C
Тангенсом острого угла прямоугольного треугольника

Соотношение в прямоугольном треугольникеABCТангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

называется отношение противолежащего катета к прилежащему.

Слайд 6 Соотношение в прямоугольном треугольнике


A
B
C
Котангенсом острого угла прямоугольного треугольника

Соотношение в прямоугольном треугольникеABCКотангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

называется отношение прилежащего катета к противолежащему.

Слайд 7 Теорема Пифагора
Теорема
В прямоугольном треугольнике квадрат гипотенузы равен

Теорема Пифагора Теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2ABCcab

сумме квадратов катетов

c2 = a2 + b2


A
B
C
c
a
b

Слайд 8 Теорема Пифагора Доказательство
Дано:
∆ACB – прямоугольный
Доказать: c2 = a2 +

Теорема Пифагора Доказательство Дано: ∆ACB – прямоугольный Доказать: c2 = a2 + b2 Доказательство:BCcabAbbbaaacccДостроим ∆ACB

b2
Доказательство:


B
C
c
a
b
A






b
b
b
a
a
a
c
c
c
Достроим ∆ACB до квадрата со стороной a + b.
Все

четыре треугольника равны по двум катетам.
Внутри квадрат, так как: 1. У него все стороны равны c. 2. <1 + <2 +<3=180° (Разв. угол) => <3=90° (ост. углы аналогично) <1 + <2=90° (Остр. Углы)
Sбольшого квадрата=(a+b)2 Sбольшого квадрата=4*½ab + c2 => (a+b)2= 4*½ab + c2 => c2 = a2 + b2



1

2

3

Слайд 9 Соотношения в прямоугольном треугольнике



А
С
B
b
c
a
ac
bc
h
ABC – прямоугольный треугольник
CH -

Соотношения в прямоугольном треугольникеАСBbcaacbchABC – прямоугольный треугольникCH - высотаh2 = acbc h

высота
h2 = acbc h = ab/c
a2 = acc b2 = bcc

Слайд 10 Медиана прямоугольного треугольника
Медиана прямоугольного треугольника, проведённая к

Медиана прямоугольного треугольника Медиана прямоугольного треугольника, проведённая к его гипотенузе, равна её половине.СABMCM - медианаCM=½AB

его гипотенузе, равна её половине.


С
A
B
M
CM - медиана
CM=½AB

  • Имя файла: bilety-ustnogo-ekzamena-po-geometrii.pptx
  • Количество просмотров: 151
  • Количество скачиваний: 0
- Предыдущая Игра Колесо истории.
Следующая - The State Emblem of the United States of America

Похожие презентации

Презентация по математике на тему Особая роль осевой симметрии Презентация по математике на тему Особая роль осевой симметрии 148
Правильные выпуклые многогранники Правильные выпуклые многогранники 167
Презентация по математике (СКК 8 вид).Площадь. Единицы площади. Презентация по математике (СКК 8 вид).Площадь. Единицы площади. 242
Синус Синус 143
Объем тел Объем тел 173
Презентация по математике на тему Теорема Пифагора Презентация по математике на тему Теорема Пифагора 157
Презентация к уроку по геометрии 9 класс Решение одной задачи Презентация к уроку по геометрии 9 класс Решение одной задачи 154
Задачи на построение сечений многогранников Задачи на построение сечений многогранников 134
Прямоугольный треугольник Прямоугольный треугольник 138
Многогранники и их история появления Многогранники и их история появления 196
Симметрия правит миром Симметрия правит миром 155
Построение диаграмм и графиков Построение диаграмм и графиков 151
Неравенство треугольника Неравенство треугольника 139
Решение тригонометрических уравнений 10 класс Решение тригонометрических уравнений 10 класс 159
Презентация для проведения КВН по математике Четырехугольники 8 класс Презентация для проведения КВН по математике Четырехугольники 8 класс 171
Презентеция Квадрат теңдеулерді шешу Презентеция Квадрат теңдеулерді шешу 250
Презентация Взаимное расположение прямой и окружности Презентация Взаимное расположение прямой и окружности 163
Презентация по геометрии на тему Треугольники (7 класс) Презентация по геометрии на тему Треугольники (7 класс) 148
Презентация к уроку геометрии в 10 классе по теме Расстояние между точками Презентация к уроку геометрии в 10 классе по теме Расстояние между точками 216
Объемы тел Объемы тел 225
Презентация по геометрии на тему Правильные многогранники Презентация по геометрии на тему Правильные многогранники 175
Угол между прямыми в пространстве Угол между прямыми в пространстве 136
Построение треугольника по трем элементам Построение треугольника по трем элементам 147
Геометрия как наука Геометрия как наука 212
Презентация к уроку геометрии в 8 классе. Презентация к уроку геометрии в 8 классе. 125
Презентация по математике Пушкин и математика Презентация по математике Пушкин и математика 165
Геометрический смысл производной Геометрический смысл производной 141
Подобные треугольники Подобные треугольники 186
Построение треугольника по трем элементам Построение треугольника по трем элементам 163
Десять решений одной задачи Десять решений одной задачи 166