- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проектная работа по геометрии по теме : Площади многоугольников
Содержание
- 2. «ЛУЧШИЙ СПОСОБ ИЗУЧИТЬ ЧТО-ЛИБО – ЭТО ОТКРЫТЬ САМОМУ.»Д. ПОЙА
- 3. ГипотезаГипотеза нашего проекта очень проста. В 8
- 4. Рабочие группы-Группа «Историки»-Группа « Практики» -Группа «Исследователи площадей многоугольников»
- 5. Задачи группГруппа «Историки»:Найти информацию о нахождении площадей
- 6. Что рассказали нам «историки»:Геометрия зародилась в Древнем
- 7. Около 600 года до н.э. ионийские греки,
- 8. Задачи царицы Дидоны Изопериметрические задачи известны также
- 9. Головоломки НаполеонаОчевидцы рассказывают, что среди прочих математических,
- 10. История головоломки "Танграм"История головоломки "Танграм"Головоломка "Танграм" -
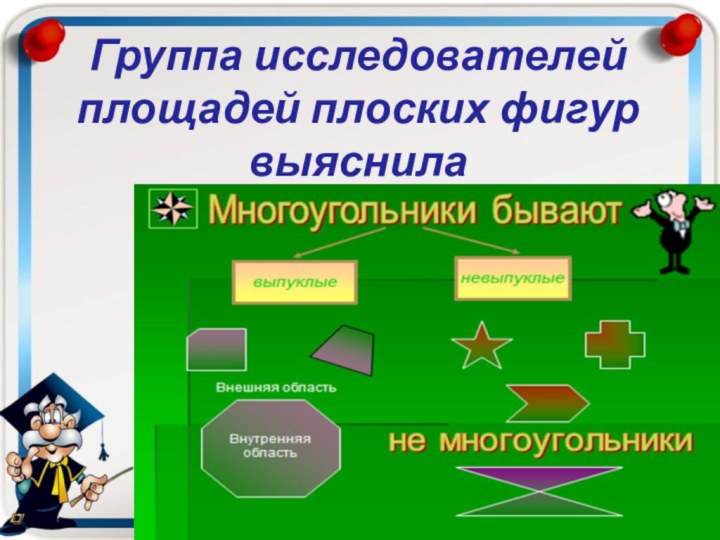
- 11. Группа исследователей площадей плоских фигур выяснила
- 12. Площадью называется величина, характеризующая размер геометрической фигуры.
- 13. Любая плоская геометрическая фигура имеет площадь
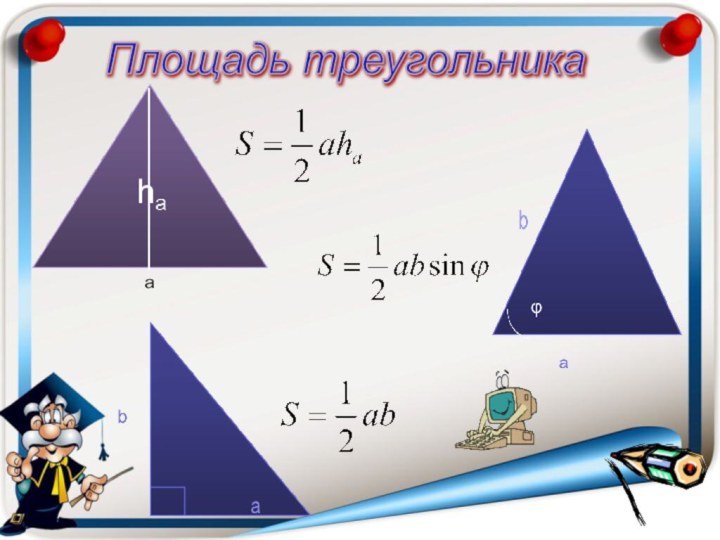
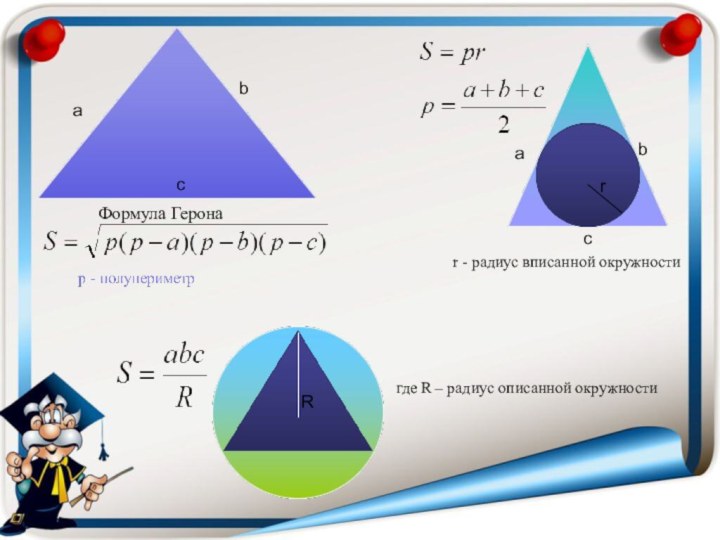
- 14. Площадь треугольника a
- 15. r - радиус вписанной окружности где R – радиус описанной окружностиФормула ГеронаabcabcRr
- 16. Площадь параллелограмма bahahbφbad1d2φ
- 17. Площадь прямоугольника aвd1d2φ
- 18. Площадь ромба ahrad1d2aaφ
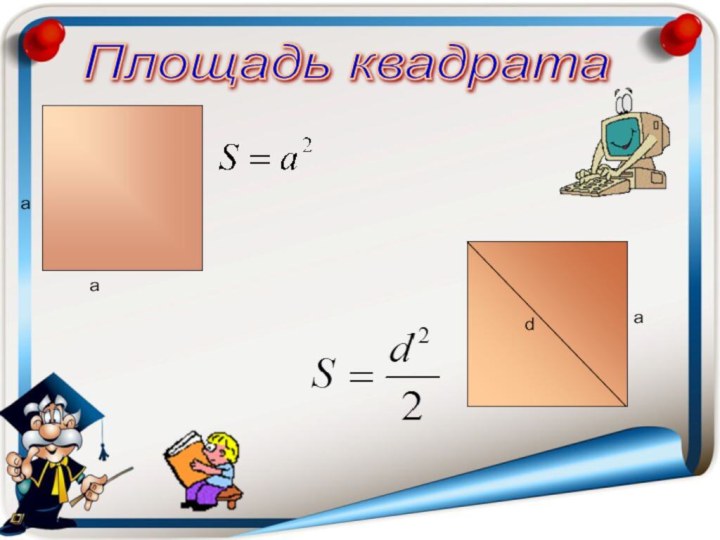
- 19. Площадь квадрата aada
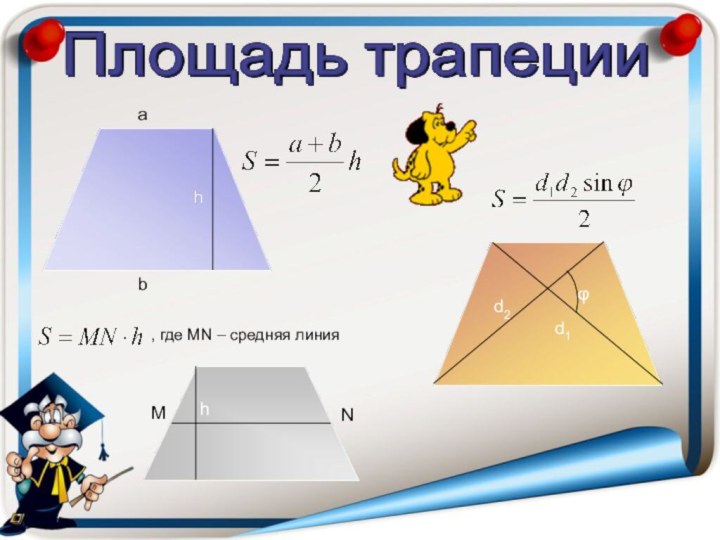
- 20. abd1d2φMNh, где MN – средняя линия
- 21. Площадь произвольного четырехугольника (для вписанного четырехугольника)(для описанного четырехугольника)
- 22. Области применения площадей многоугольников В строительстве;В
- 23. Французский архитектор Ле Корбюзье «Человеку , сведущему
- 27. Площади в географии
- 28. Немного истории об оригамиОригами- древнейшее искусство складывание
- 29. Поделки «оригами»
- 31. Используемая литература1. «Геометрия 7 - 9 класс».
- 32. Скачать презентацию
- 33. Похожие презентации
«ЛУЧШИЙ СПОСОБ ИЗУЧИТЬ ЧТО-ЛИБО – ЭТО ОТКРЫТЬ САМОМУ.»Д. ПОЙА



























Слайд 3
Гипотеза
Гипотеза нашего проекта очень проста. В 8 классе
мы познакомились с четырёхугольниками и узнали о них много
интересного. В этом году, когда мы начали изучать пощади многоугольников, но само определение площади нам было не очень понятным. Нас заинтересовал этот вопрос, ведь геометрия- наука древняя, это наука, которая изучает свойства геометрических фигур. Слово «геометрия»- в переводе с греческого означает «землемерие». Возник вопрос о времени образования понятия «площадь», о её применении. Мы решили более подробно узнать об этом. У нас организовались три группы, которые получили определённое задание.
Слайд 4
Рабочие группы
-Группа «Историки»
-Группа « Практики»
-Группа «Исследователи площадей многоугольников»
Слайд 5
Задачи групп
Группа «Историки»:
Найти информацию о нахождении площадей древними
учёными.
Группа « Практики»:
1. Найти материал, подтверждающий применение площадей
в архитектуре и строительстве.
2. Найти материал, подтверждающий применение площадей в географии.Группа «Исследователи площадей многоугольников»:
Изучить доказательства площадей треугольника, квадрата, прямоугольника и трапеции
Слайд 6
Что рассказали нам «историки»:
Геометрия зародилась в Древнем Египте
где-то в 1700 году до н.э. Во время сезона
тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянам стали такие виды их деятельности, как возведение пирамид и изобразительное искусство. Египтяне при применении геометрических знаний всецело руководствовались интуицией и приближенными представлениями.Египет
Слайд 7 Около 600 года до н.э. ионийские греки, совершившие
путешествие в Египет, привезли на родину первые сведенья о
геометрии. Самым известным путешественником в Египет был Фалес (ок. 640-ок.546 до н.э.). Он был преуспевающим купцом, посвятившим последние годы жизни науке и политике. Фалес первым начал доказывать истинность геометрических соотношений.Греция
Слайд 8
Задачи царицы Дидоны
Изопериметрические задачи известны также под
названием “задачи Дидоны” по имени легендарной основательницы города Карфагена
и его первой царицы. Согласно легенде, вынужденная бежать из своего родного города, царица Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей место для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узенькие ремешки и, разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было бы покрыть шкурой целиком.
Слайд 9
Головоломки Наполеона
Очевидцы рассказывают, что среди прочих математических, шахматных
и тактических задач по военному искусству император Наполеон любил
задавать своим офицерам и эту головоломку: какие плоские геометрические фигуры можно построить из девяти предложенных в россыпь деталей
Слайд 10
История головоломки "Танграм"
История головоломки "Танграм"
Головоломка "Танграм" - квадрат,
разрезанный на 7 частей из которых составляют различные силуэты.
Он появился в Китае в конце восемнадцатого века (рисунок). Первое ее изображение (1780 г.) обнаружено на ксилографии японского художника Утамаро, где две девушки складывают фигурки "чи чао ту" - так называется ташрам на его родине (в переводе - умственная головоломка из семи частей"). Название танграм возникло в Европе вероятнее всего от слова "тань" (на кантонском диалекте - китаец) и часто встречающегося греческого корня "грамма" (буква). Впрочем, авторы многих книг по занимательной математике приписывают изобретение танграма якобы жившему 4 тысячи лет назад в Китае ученому Тангу. Эта тщательно разработанная легенда от начала до конца выдумана изобретательным автором головоломок Сэмом Лойдом.Слайд 12 Площадью называется величина, характеризующая размер геометрической фигуры. Определение
площадей геометрических фигур – одна из древнейших практических задач.
Правильный подход к их решению был найден не сразу. Древние греки умели правильно находить площади многоугольников. Когда каменщики определяют площадь прямоугольной стены дома они перемножают высоту и ширину стены. Долгий был путь к нахождению формул, позволяющим найти площади любых фигур. В настоящее время существуют и механические приборы для вычисления площадей плоских фигур – так называемые планиметры.
Слайд 21
Площадь произвольного четырехугольника
(для вписанного четырехугольника)
(для описанного четырехугольника)
Слайд 22
Области применения площадей многоугольников
В строительстве;
В архитектуре;
В машиностроении;
В
сельском хозяйстве;
В географии ;
В искусстве и т. д.
Слайд 23
Французский архитектор Ле Корбюзье
«Человеку , сведущему в
геометрии и работающему с нею, становятся доступны…все те высшие
наслаждения, которые называются наслаждениями математического порядка…Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Стоит поразмыслить о прошлом, вспомнить то, что было ранее, и мы будем ошеломлены, видя, что окружающий нас мир- это мир геометрии, чистой, истинной, в наших глазах. Всё вокруг- геометрия. Никогда мы не видели так ясно таких форм, как круг, прямоугольник, угол, цилиндр, шар, выполненных так отчётливо, с такой тщательностью и так уверенно»
Слайд 28
Немного истории об оригами
Оригами- древнейшее искусство складывание из
бумаги различных объемных фигурок.
Возникло 2000 лет тому назад в
Китае.В 7 веке оригами было известно в Японии.
Слайд 31
Используемая литература
1. «Геометрия 7 - 9 класс». Авторы
– А. В. Погорелов
2. «Математическая энциклопедия» Авторы - М.
Ю. Серебряков, Л. В. Кузнецов3. «История математики в школе.VII- VIII классы». Автор- Г.И. Глейзер.
4. «Математика в понятиях, определениях и терминах» Авторы- О. В. Мантуров и др.
5.Интернет ресурсы.
6.Развивающие задачи по геометрии 8-9 классы-Н.М. Карпушина