помощью специальных знаков – цифр.
Числа:
123, 45678, 1010011, CXL
Цифры:
0, 1,
2, … I, V, X, L, …Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Типы систем счисления:
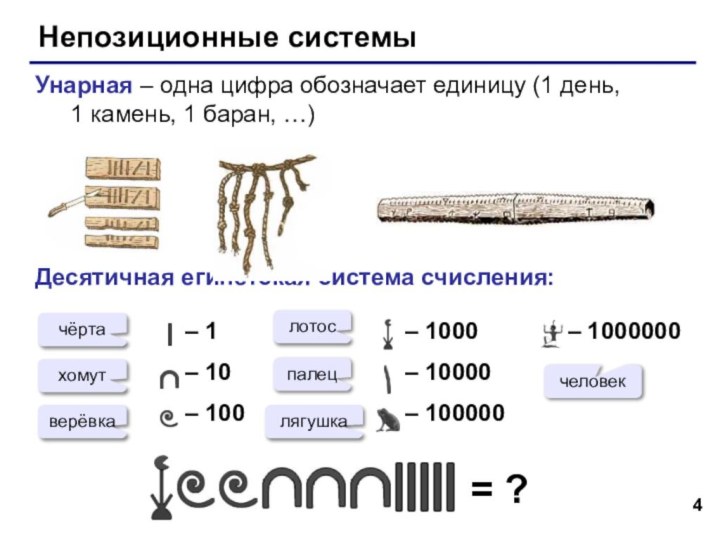
непозиционные – значение цифры не зависит от ее места (позиции) в записи числа;
позиционные – зависит…