- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике: Правила перевода чисел из одной системы счисления в другую (8 класс)
Содержание
- 2. Цель урока:Научиться самостоятельно выполнять перевод десятичных чисел
- 3. Системы счисления Система счисления
- 4. Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную
- 5. Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную
- 6. Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную
- 7. Физкультминутка
- 8. Чтобы перевести число из двоичной системы в
- 9. Для перевода восьмеричного числа в двоичное необходимо
- 10. ТЕСТконтроль знаний
- 11. 1)Что такое система счисления?А) это знаковая система,
- 12. РефлексияНа стикерах напишите свои ощущения за урок,
- 13. Спасибо за урок
- 14. Что такое система счисления? ( система счисления
- 15. Позиционные системы счисления
- 16. Основание системы счисления Количество различных
- 17. Основание системы счисленияКомпьютеры используют двоичную систему так
- 18. Основание системы счисления Запись чисел
- 19. Соответствие систем счисленияназадВ меню
- 20. Перевод целых чисел из десятичной системы
- 21. Перевод целых чисел из десятичной системы
- 22. Перевод целых чисел из десятичной системы
- 23. Перевод правильной десятичной дроби из десятичной системы
- 24. Перевод правильной десятичной дроби из десятичной системы
- 25. Перевод вещественных чисел из десятичной системы счисления
- 26. Перевод вещественных чисел из десятичной системы счисления
- 27. Перевод вещественных чисел из десятичной системы счисления
- 28. Перевод вещественных чисел из десятичной системы счисления
- 29. Перевод чисел в десятичную систему счисления
- 30. Перевод чисел в десятичную систему счисления
- 31. Перевод из восьмеричной и шестнадцатеричной системы счисления
- 32. Перевод из двоичной системы счисления в восьмеричную
- 33. Перевод из восьмеричной системы счисления в шестнадцатеричную
- 34. Арифметические операции в позиционных системах счисления
- 35. Арифметические операции в позиционных системах счисления
- 36. Сложение в позиционных системах счисления
- 37. Вычитание в позиционных системах счисления
- 38. 3∙3=9=8+1Умножение в позиционных системах счисления
- 39. Деление в позиционных системах счисления
- 40. Представление чисел в компьютере
- 41. Представление целых чисел в компьютере
- 42. Представление целых чисел в компьютере
- 43. Представление целых чисел в компьютереПример. Число 6210
- 44. Представление целых чисел в компьютереПример. Число -5710
- 45. Представление целых чисел в компьютереПример. Число -5710
- 46. Представление целых чисел в компьютереПример. Число -5710
- 47. Представление целых чисел в компьютереОтрицательные десятичные числа
- 48. Представление вещественных чисел в компьютереЛюбое число N
- 49. Представление вещественных чисел в компьютереФорматы вещественных чисел
- 50. Представление вещественных чисел в компьютереПри хранении числа
- 51. Представление вещественных чисел в компьютереПример. Число 6,2510
- 52. Скачать презентацию
- 53. Похожие презентации














































Слайд 2
Цель урока:
Научиться самостоятельно выполнять перевод десятичных чисел в
двоичную, восьмеричную, шестнадцатеричную систему счисления и обратно.
ранее полученные знания о системах счисления
Слайд 3
Системы счисления
Система счисления –
это знаковая система, в которой числа записываются по определённым
правилам с помощью символов некоторого алфавита, называемых цифрамиКоличественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
0,7 7 70
Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
XIX
Позиционные
Непозиционные
Системы
счисления
Слайд 4 Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную систему
Для перевода десятичного числа в двоичную систему его необходимо
последовательно делить на ___ до тех пор, пока не останется ________, меньший или равный __. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в _________ порядке.2
остаток
1
обратном
Пример. Число 2210 перевести в двоичную систему счисления.
Ответ: 2210 = 10110 2
Задание №1: Переведите целые числа из десятичной системы счисления в двоичную
76; 121
Ответ: 7610 = 1001002
12110 = 11012
Слайд 5 Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную систему
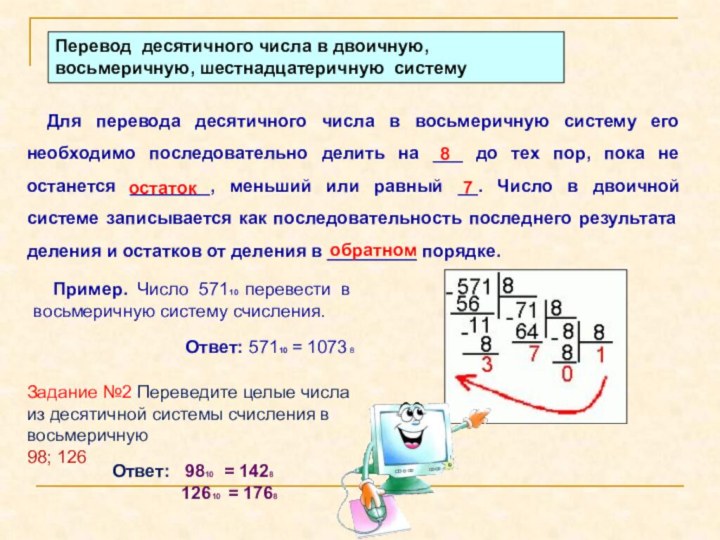
Для перевода десятичного числа в восьмеричную систему его необходимо
последовательно делить на ___ до тех пор, пока не останется ________, меньший или равный __. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в _________ порядке.8
остаток
7
обратном
Пример. Число 57110 перевести в восьмеричную систему счисления.
Ответ: 57110 = 1073 8
Задание №2 Переведите целые числа из десятичной системы счисления в восьмеричную
98; 126
Ответ: 9810 = 1428
12610 = 1768
Слайд 6 Перевод десятичного числа в двоичную, восьмеричную, шестнадцатеричную систему
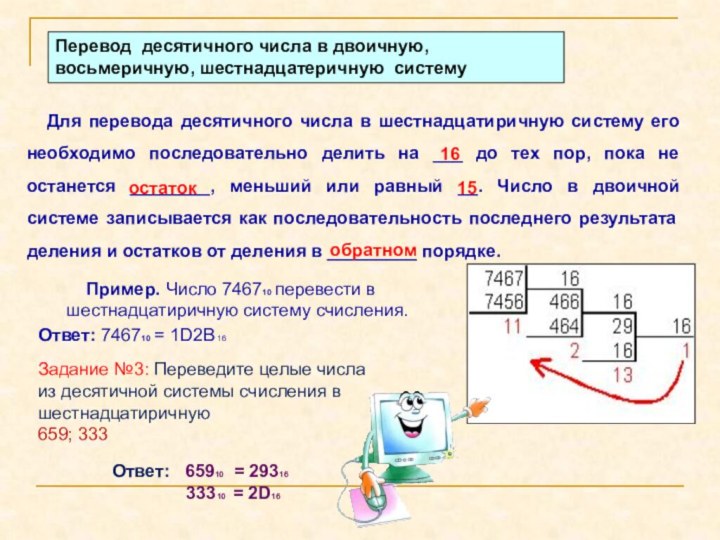
Для перевода десятичного числа в шестнадцатиричную систему его необходимо
последовательно делить на ___ до тех пор, пока не останется ________, меньший или равный __. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в _________ порядке.16
остаток
15
обратном
Пример. Число 746710 перевести в шестнадцатиричную систему счисления.
Ответ: 746710 = 1D2B 16
Задание №3: Переведите целые числа из десятичной системы счисления в шестнадцатиричную
659; 333
Ответ: 65910 = 29316
33310 = 2D16
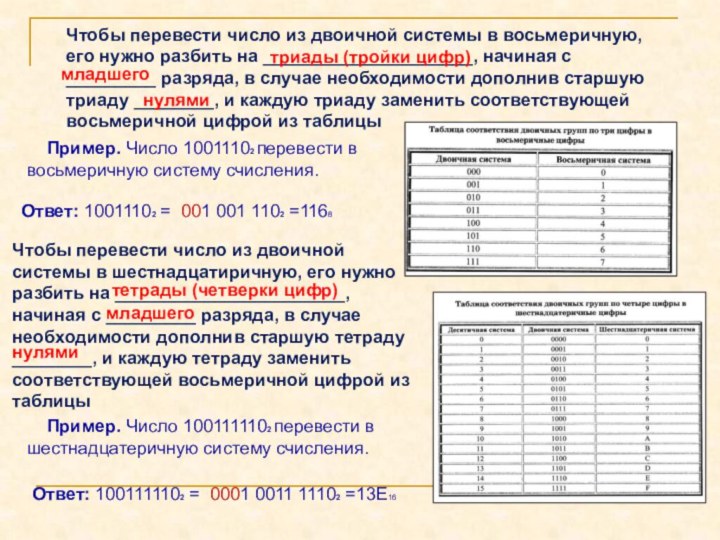
Слайд 8 Чтобы перевести число из двоичной системы в восьмеричную,
его нужно разбить на _____________________, начиная с _________ разряда,
в случае необходимости дополнив старшую триаду ________, и каждую триаду заменить соответствующей восьмеричной цифрой из таблицытриады (тройки цифр)
младшего
нулями
Пример. Число 10011102 перевести в восьмеричную систему счисления.
Ответ: 10011102 = 001 001 1102 =1168
Чтобы перевести число из двоичной системы в шестнадцатиричную, его нужно разбить на _______________________, начиная с _________ разряда, в случае необходимости дополнив старшую тетраду ________, и каждую тетраду заменить соответствующей восьмеричной цифрой из таблицы
тетрады (четверки цифр)
младшего
нулями
Пример. Число 1001111102 перевести в шестнадцатеричную систему счисления.
Ответ: 1001111102 = 0001 0011 11102 =13Е16
Слайд 9 Для перевода восьмеричного числа в двоичное необходимо каждую
цифру заменить эквивалентной ей двоичной триадой.
Пример. Число 5318
перевести в двоичную систему счисления Ответ: 5318 = 1010110012
Задание №4: Переведите следующие числа:
1) 100011111110002 А8 2) 110000111112 А8
3) 1111111111000002 А16 4) 011000111002 А16
Ответ: 1)=217708 2)=30378
3)=7FE016 4)=31C16
Слайд 11
1)Что такое система счисления?
А) это знаковая система, в
которой числа записываются по определённым правилам с помощью символов
некоторого алфавита, называемых цифрами.В) это знаковая цифровая система, в которой знаки записываются по определённым правилам.
С) это знаковая система, в которой числа записываются в свободном порядке с помощью символов.
2) На какие группы делятся системы счисления?
А) позиционные и цифровые
В) непозиционные и цифровые
С) позиционные и непозиционные
3) Какая система счисления называется позиционной?
А) смысл цифры числа не зависит от занимаемой ею позиции, римская система.
В) значение цифры зависит от ее места
С) нет верного ответа
4) Какая система счисления называется непозиционной?
А) смысл цифры числа не зависит от занимаемой ею позиции, римская система.
В) значение цифры зависит от ее места
С) нет верного ответа
5) Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на……..
А) триады
В) тетрады
С) нет верного ответа
6) Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на……
А) триады
В) тетрады
С) нет верного ответа
7) в случае необходимости дополнить старшую тетраду или триаду …..
А) нулями
В) единицами
С) нулями или единицами
Ключ к тесту: 1) А; 2) С; 3) В; 4) А; 5) В; 6) А; 7) А;
Слайд 12
Рефлексия
На стикерах напишите свои ощущения за урок, и
прикрепите к той картинке, которая отражает ваше настроение в
данный момент.У меня все получилось! Мне все понравилось.
Так, над эти нужно подумать.
Мне было трудно, я ничего не понял.
Слайд 14
Что такое система счисления? ( система счисления –
это знаковая система, в которой числа записываются по определённым
правилам с помощью символов некоторого алфавита, называемых цифрами)На какие группы делятся системы счисления? ( позиционные и непозиционные)
Какая система счисления называется позиционной? Привести пример ( система счисления, в которой значение любой цифры не зависит от занимаемой ею позиции. Например, римская система счисления)
Какая система счисления называется позиционной? ( система счисления, в которой значение любой в числе зависит от её положения в ряду цифр, изображающих это число. Например, десятичная система счисления)
Слайд 15
Позиционные системы счисления
Первая
позиционная система счисления была придумана еще в Древнем Вавилоне,
причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр!В XIX веке довольно широкое распространение получила двенадцатеричная система счисления.
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
«Мысль – выражать все числа немногими знаками, придавая им значение по форме, ещё значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна»
Пьер Симон Лапласс
Слайд 16
Основание системы счисления
Количество различных символов,
используемых для изображения числа в позиционных системах счисления, называется
основанием системы счисления.Позиции цифр называются разрядами.
Основание системы счисления показывает во сколько раз изменяется количественное значение цифры при перемещении её на соседнюю позицию
За основание системы можно принять любое натуральное число не менее 2.
Слайд 17
Основание системы счисления
Компьютеры используют двоичную систему так как
для её реализации нужны технические устройства с двумя устойчивыми
состояниями,представление информации с помощью только двух состояний надежно и помехоустойчиво,
возможно применение аппарата булевой алгебры для выполнения логических преобразований,
двоичная арифметика намного проще десятичной
Двоичная система, удобная для компьютера, для человека неудобна из-за её громоздкости и непривычной записи. Для того, чтобы понимать слово компьютера, разработаны восьмеричная и шестнадцатеричная системы счисления. Числа в этих системах требуют в 3/4 раза меньше разрядов, чем в двоичной системе.
Слайд 18
Основание системы счисления
Запись чисел в
каждой из систем счисления с основанием q означает сокращенную
запись выраженияan-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m ,
где ai – цифры системы счисления, n и m –число целых и дробных разрядов соответственно
Слайд 20
Перевод целых чисел из
десятичной системы счисления
Алгоритм перевода:
Последовательно
делить с остатком данное число и получаемые целые частные
на основание новой системы счисления до тех пор, пока частное не станет равно нулю.Полученные остатки выразить цифрами алфавита новой системы счисления
Записать число в новой системе счисления из полученных остатков, начиная с последнего.
Слайд 21
Перевод целых чисел из
десятичной системы счисления
Пример. Перевести число 75 из десятичной системы счисления в
двоичную, восьмеричную и шестнадцатеричную.75
2
74
1
37
2
36
1
18
2
18
0
9
2
8
1
4
2
4
0
2
2
2
0
2
1
0
0
1
7510 = 10010112
Слайд 22
Перевод целых чисел из
десятичной системы счисления
Пример 1. Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную.75
8
72
3
9
8
8
1
1
8
0
1
0
7510 = 1138
75
16
64
11
4
16
0
4
0
7510 = 4B16
В меню
Слайд 23
Перевод правильной десятичной дроби из десятичной системы счисления
Алгоритм
перевода:
Последовательно умножать десятичную дробь и получаемые дробные части произведений
на основание новой системы счисления до тех пор, пока дробная часть не станет равна нулю или не будет достигнута необходимая точность перевода.
Полученные целые части произведений выразить цифрами алфавита новой системы счисления.
Записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
Слайд 24
Перевод правильной десятичной дроби из десятичной системы счисления
Пример.
Перевести число 0,35 из десятичной системы в счисления в
двоичную, восьмеричную и шестнадцатеричную.0,35
2
0,70
2
1,40
2
0,80
2
1,60
2
1,20
0,3510 = 0,010112
0,35
8
2,80
8
6,40
8
3,20
0,3510 = 0,2638
0,35
16
5,60
16
9,60
0,3510 = 0,5916
В меню
Слайд 25
Перевод вещественных чисел из десятичной системы счисления
При переводе смешанных дробей отдельно по своим правилам
переводятся целая и дробные части, результаты перевода разделяются запятой.
Слайд 26
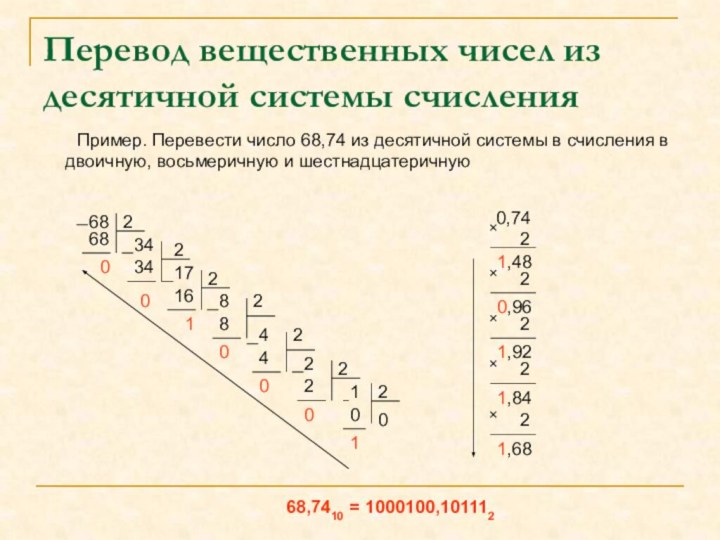
Перевод вещественных чисел из десятичной системы счисления
Пример. Перевести число 68,74 из десятичной системы в
счисления в двоичную, восьмеричную и шестнадцатеричную68
2
68
0
34
2
34
0
17
2
16
1
8
2
8
0
4
2
4
0
2
2
2
0
2
1
0
0
1
0,74
2
1,48
2
0,96
2
1,92
2
1,84
2
1,68
68,7410 = 1000100,101112
Слайд 27
Перевод вещественных чисел из десятичной системы счисления
Пример. Перевести число 68,74 из десятичной системы в
счисления в двоичную, восьмеричную и шестнадцатеричную68
8
64
4
8
8
8
0
1
8
0
1
0
0,74
8
5,92
8
7,36
8
2,88
68,7410 = 104,5728
Слайд 28
Перевод вещественных чисел из десятичной системы счисления
Пример. Перевести число 68,74 из десятичной системы в
счисления в двоичную, восьмеричную и шестнадцатеричную68
16
64
4
4
16
0
4
0
0,74
16
11,84
16
13,44
68,7410 = BD8
В меню
Слайд 29
Перевод чисел в десятичную систему счисления
При
переводе числа из системы счисления с основанием q в
десятичнуюнадо представить это число в виде суммы произведений степеней
основания его системы счисления q на соответствующие цифры числа.
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m
и выполнить арифметические вычисления.
Слайд 30
Перевод чисел в десятичную систему счисления
Пример.
Перевести число 1011,1 из двоичной системы счисления в десятичную.
1
0 1 1, 12-1
0
1
2
3
= 1∙23 + 0∙22 + 1∙21 + 1∙20 + 1∙2-1 = 11,510
разряды
число
Пример. Перевести число 276,8 из восьмеричной системы счисления в десятичную.
2 7 6, 58
-1
0
1
2
= 2∙82 + 7∙81 + 6∙80 + 5∙8-1 = 190,62510
разряды
число
Пример. Перевести число 1F3 из шестнадцатеричной системы счисления в десятичную.
1 F 316
0
1
2
= 1∙162 + 15∙161 + 3∙160 = 49910
разряды
число
В меню
Слайд 31 Перевод из восьмеричной и шестнадцатеричной системы счисления в
двоичную
Заменить каждую цифру восьмеричного/шестнадцатеричного числа соответствующим
трехразрядным/четырехразрядным двоичным кодом.Пример. Перевести число 527,18 в двоичную систему счисления.
527,18 =
101
010
111,
001
5
2
7
1
2
Пример. Перевести число 1A3,F16 в двоичную систему счисления.
1A3,F16 =
0001
1010
0011,
1111
1
A
3
F
2
Таблица соответствия
В меню
Слайд 32 Перевод из двоичной системы счисления в восьмеричную и
шестнадцатеричную
Для перехода от двоичной к восьмеричной/шестнадцатеричной
системе счисления поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по 3/4 разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из 3/4 разрядов заменяют соответствующей восьмеричной/шестнадцатеричной цифрой.Пример
1 0 1 0 1 0 0 1,1 0 1 1 1 2
1
5
0
6
0
2
5
= 251,658
1 0 1 0 1 0 0 1,1 0 1 1 1 2
9
B
A
000
8
= A9,B816
Таблица соответствия
В меню
Слайд 33 Перевод из восьмеричной системы счисления в шестнадцатеричную и
обратно
При переходе из восьмеричной системы счисления
в шестнадцатеричную и обратно вначале производится перевод чисел из исходной системы счисления в двоичную, а затем – в конечную систему .Пример. Перевести число 527,18 в шестнадцатеричную систему счисления.
527,18 =
Пример. Перевести число 1A3,F16 в восьмеричную систему счисления.
1A3,F16 =
101010111,011 2
7
6
0
5
=157,616
000
1
110100011,1111 2
3
7
4
00
6
4
=643,748
Таблица соответствия
В меню
самостоятельные задания
Слайд 34
Арифметические операции в позиционных системах счисления
Правила выполнения основных арифметических операций в любой позиционной
системе счисления подчиняются тем же законам, что и в десятичной системе.При сложении цифры суммируются по разрядам, и если при этом возникает переполнение разряда, то производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления.
При вычитании из меньшей цифры большей в старшем разряде занимается единица, которая при переходе в младший разряд будет равна основанию системы счисления
Слайд 35
Арифметические операции в позиционных системах счисления
Если при умножении однозначных чисел возникает переполнение разряда,
то в старший разряд переносится число кратное основанию системы счисления. При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления.Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе, то есть сводится к операциям умножения и вычитания.
Слайд 36
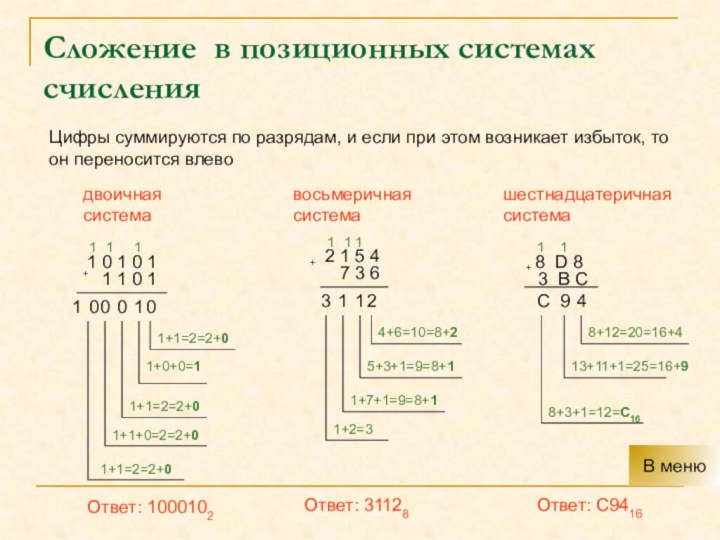
Сложение в позиционных системах счисления
Цифры суммируются по разрядам, и если при этом возникает
избыток, то он переносится влево 1 0 1 0 1
+
1 1 0 1
двоичная
система
0
1+1=2=2+0
1
1
1+0+0=1
0
1+1=2=2+0
1
0
1+1+0=2=2+0
1
0
1+1=2=2+0
1
Ответ: 1000102
2 1 5 4
+
7 3 6
2
4+6=10=8+2
1
1
5+3+1=9=8+1
1
1+7+1=9=8+1
1
3
1+2=3
восьмеричная
система
1
Ответ: 31128
шестнадцатеричная
система
8 D 8
+
3 B C
4
8+12=20=16+4
1
9
13+11+1=25=16+9
8+3+1=12=C16
C
1
Ответ: C9416
В меню
Слайд 37
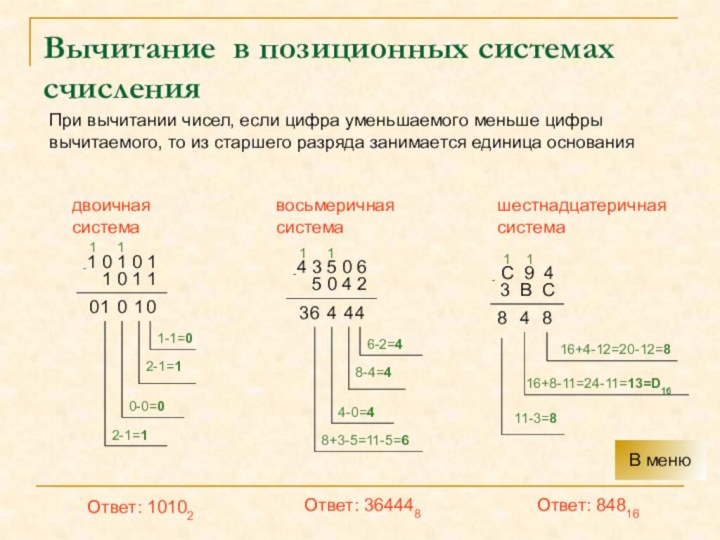
Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого,
то из старшего разряда занимается единица основаниядвоичная
система
Ответ: 10102
восьмеричная
система
Ответ: 364448
шестнадцатеричная
система
Ответ: 84816
1 0 1 0 1
-
1 0 1 1
0
1-1=0
1
1
2-1=1
0
0-0=0
1
2-1=1
1
0
4 3 5 0 6
-
5 0 4 2
4
6-2=4
1
4
8-4=4
4
4-0=4
6
8+3-5=11-5=6
1
3
С 9 4
-
3 В С
8
16+4-12=20-12=8
1
4
16+8-11=24-11=13=D16
8
11-3=8
1
В меню
Слайд 38
3∙3=9=8+1
Умножение в позиционных системах счисления
При умножении многозначных чисел в различных позиционных системах применяется
алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счислениядвоичная
система
Ответ: 1010111112
восьмеричная
система
Ответ: 133518
1 1 0 1 1
х
1 1 0 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 0 1 1 1 1 1
1+1+1=3=2+1
1
1+1+1=3=2+1
1
1+1=2=2+0
1
1
1 6 3
х
6 3
5 3 1
1
6∙3+1=19=16+3=2∙8+3
2
1∙3+2=5
1 2 6 2
6∙3=18=16+2=8∙2+2
6∙6+2=38=32+6=4∙8+6
2
4
6∙1+4=10=8+2
1 3 3 5 1
6+5=11=8+3
1
В меню
самостоятельные задания
Слайд 39
Деление в позиционных системах счисления
Деление в любой позиционной системе производится по тем же
правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.двоичная
система
Ответ: 10,12
восьмеричная
система
Ответ: 638
1 0 0 0 1 1
1 1 1 0
1
1 1 1 0
1 1 1 0
1 1
1
,
0
0
1
0
1 3 3 5 1
1 6 3
6
1 2 6 2
5 3
1
3
5 3 1
0
В меню
самостоятельные задания
Слайд 40
Представление чисел в компьютере
Числа
в компьютере могут храниться в формате с фиксированной
запятой – целые числа и в формате с плавающей запятой – вещественные числа. Целые числа без знака занимают в памяти один или два байта.
Целые числа со знаком занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа
Применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код.
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. Этот формат базируется на экспоненциальной форме записи, в которой может быть представлено любое число
Слайд 41
Представление целых чисел в компьютере
Целые
числа в компьютере могут представляться со знаком или без
знака.Целые числа без знака занимают в памяти один или два байта.
Пример. Число 7210 = 10010002 в однобайтовом формате
Слайд 42
Представление целых чисел в компьютере
Целые числа со знаком занимают в памяти компьютера один,
два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» - единицей
Слайд 43
Представление целых чисел в компьютере
Пример. Число 6210 =
1111102 в однобайтовом формате
В компьютерной технике применяются три формы
записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код.Положительные числа в прямом, обратном и дополнительных кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.
Знак числа
Слайд 44
Представление целых чисел в компьютере
Пример. Число -5710 =
-1110012 в однобайтовом формате
Отрицательные числа в прямом, обратном
и дополнительных кодах имеют разное изображение..Знак числа
Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.
прямой код
Слайд 45
Представление целых чисел в компьютере
Пример. Число -5710 =
-1110012 в однобайтовом формате
Знак числа
Обратный код. Для образования
обратного кода отрицательного двоичного числа необходимо в знаковом разряде поставить 1, а в цифровых разрядах единицы заменить нулями, а нули - единицами.обратный код
Слайд 46
Представление целых чисел в компьютере
Пример. Число -5710 =
-1110012 в однобайтовом формате
Знак числа
Дополнительный код отрицательного числа
получается образованием обратного кода с последующим прибавлением единицы к его младшему разрядудополнительный код
Слайд 47
Представление целых чисел в компьютере
Отрицательные десятичные числа при
вводе в компьютер автоматически преобразуются в обратный или дополнительный
код и в таком виде хранятся, перемещаются и участвуют в операциях.При выводе таких чисел из компьютера происходит обратное преобразование в отрицательные десятичные числа
В меню
Слайд 48
Представление вещественных чисел в компьютере
Любое число N в
системе счисления с основанием q можно записать в виде
N = m ∙ q p, где М называется мантиссой числа, а р – порядком.Такой способ записи чисел называется представлением числа с плавающей точкой
Данное представление вещественных чисел называется нормализованным.
Мантиссу и порядок q-ичного числа записывают в системе счисления с основанием q, а само основание – в десятичной системе
Мантисса должна быть правильной дробью, первая цифра которой отлична от нуля.
Слайд 50
Представление вещественных чисел в компьютере
При хранении числа с
плавающей точкой отводятся разряды для мантиссы, порядка, знака числа
и знака порядказнак числа
знак порядка
порядок
мантисса
Слайд 51
Представление вещественных чисел в компьютере
Пример. Число 6,2510 записать
в нормализованном виде в четырехбайтовом формате с семью разрядами
для записи порядка6,2510 = 110,012 = 0,11001 ∙ 211
знак числа
знак порядка
порядок
мантисса
31
30
22
0
0
1
1
0
0
0
1
1
1
0
0
0
0