Презентация на тему Подготовка к ЕГЭ_разбор задач_Стратегия

игрока убирают спички по очереди, причем за 1 ход

можно убрать 1 или 2 спички;
выигрывает тот, кто оставит в кучке 1 спичку

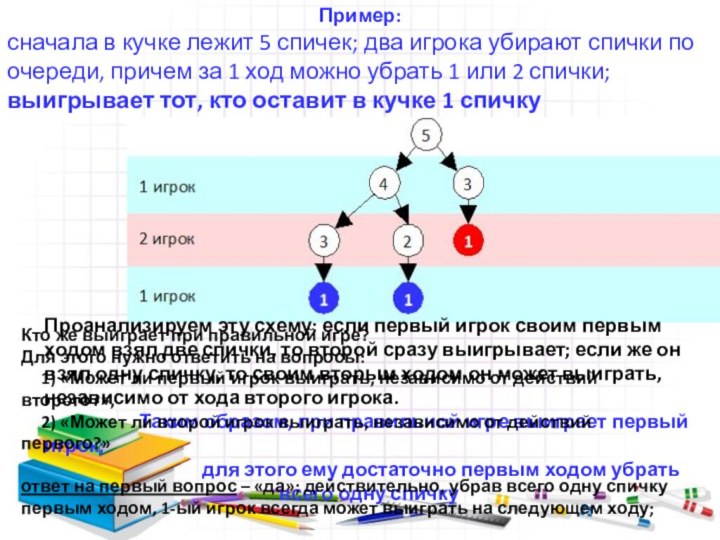
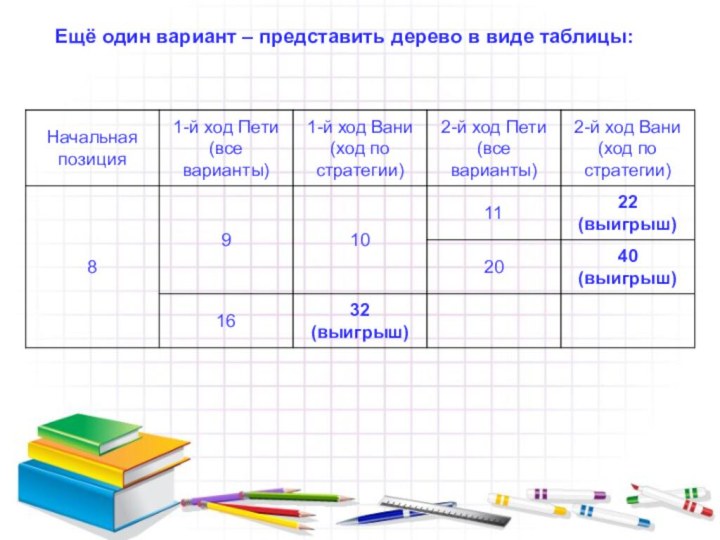
Проанализируем эту схему: если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока.
Таким образом, при правильной игре выиграет первый игрок;
для этого ему достаточно первым ходом убрать
всего одну спичку

Кто же выиграет при правильной игре?
Для этого нужно ответить на вопросы:
1) «Может ли первый игрок выиграть, независимо от действий второго?»,
2) «Может ли второй игрок выиграть, независимо от действий первого?»

ответ на первый вопрос – «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу;

ответ на второй вопрос – «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется

и проигрышные
выигрышная позиция – это такая позиция, в которой

игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии;
таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
выигрышные и проигрышные позиции можно охарактеризовать так:
позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная, при этом стратегия игрока
состоит в том, чтобы перевести игру в эту
проигрышную (для соперника) позицию.

«+1» или «*2».

Выиграть последним ходом «+1» можно, если S = 21.
Ходом «*2» можно выиграть из любой позиции при S > 10 (сюда входит и 21!).
Можно составить таблицу, в которой «В1» обозначает выигрыш за один ход:

S

Поэтому ответ должен быть такой:
«Петя может выиграть за один ход при любом S > 10. Он должен увеличить вдвое число камней, при этом в куче всегда получится не менее 22 камней.»

не может выиграть за один ход, но при любом

ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.




Ответ должен быть такой:
«При S = 10 Петя не может выиграть в один ход, потому что при его ходе «+1» число камней в куче становится равно 11 (меньше 22), а при ходе «*2» число камней в куче становится равно 20 (также меньше 22). Других возможных ходов у Пети нет. Из любой позиции после одного хода Пети (это может быть 11 или 20), Ваня может выиграть своим первых ходом, удвоив количество камней в куче.»

у Пети есть выигрышная стратегия, причём – Петя не может

выиграть за один ход, и – Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную стратегию Пети.

Поэтому ответ должен быть такой:
«Из позиций S = 9 и S = 5 Петя не может выиграть в один ход, но Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.
При S = 9 ходом «+1» Пете нужно перевести игру в позицию S = 10, которая является проигрышной (см. ответ на вопрос 1б).
При S = 5 Петя переводит игру в ту же позицию ходом «*2».»

есть выигрышная стратегия, позволяющая ему выиграть первым или вторым

ходом при любой игре Пети, и – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.



Поэтому ответ должен быть такой:
« В позиции S = 8 у Вани есть выигрышная стратегия, которая позволяет ему выиграть первым или вторым ходом. Если Петя выбирает ход «+1», в куче становится 9 камней и Ваня выигрывает на 2-м ходу (см. ответ на вопрос 2). Если Петя выбирает ход «*2», Ваня выигрывает первым ходом, удвоив число камней в куче.»

S = 8.
Для этого используем построенную таблицу:
Здесь красным

цветом выделены позиции, в которых игра заканчивается.

например, «положив его на бок»

таблицы:

индустриальный университет»,
кафедра информационных систем и технологий
Факультет довузовского

образования МГИУ;
Кафедра информатики МФТИ
Интернет: http://live.msiu.ru/fdo. Почта: fdo@msiu.ru.

http://www.youtube.com/watch?v=1BNpvLdD7Bg
http://www.youtube.com/watch?v=5uPAbfmjzX8
http://www.youtube.com/watch?v=JNuGs-cXaoI
http://www.youtube.com/watch?v=G9CY2-ZcKnY
http://www.youtube.com/watch?v=dwyWw4I4A5s

какая часть IP-адреса узла сети относится к адресу сети,

а какая – к адресу самого узла в этой сети.
Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.
IP-адрес узла: 64.128.208.194
Маска: 255.255.224.0 При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в нужном порядке соответствующие им буквы без использования точек.

Разбор задачи B11

HBAF.                                                                                        

в двоичную систему счисления
                                                            

4) Получившиеся октеты переводим обратно

в десятичную систему счисления
                                                            

5) По таблице ищем совпадения и выписываем
соответствующие буквы.
Их и записываем в ответ
                                                            

2) Переводим каждый октет IP-адреса в двоичную систему счисления
                                                            

Если число в двоичной системе счисления получилось   маленьким  (меньше 8 знаков), значит, добавляем слева нули                                                        

3) Выполняем конъюнкцию соответствующих элементов
                                                            

счисления
6410 = 10000002, добавляем 0

до 8 знаков, будет 010000002.
12810 = 100000002. 20810 = 110100002. 19410 = 110000102.                                                             

3) Выполняем конъюнкцию
При конъюнкции числа 11111111 с любым другим числом всегда будет получаться тоже число. (Поэтому можно было и не переводить октеты 255 в двоичную систему). Выполняем конъюнкцию маски с IP-адресом: 11100000 /\ 11010000 (всегда: 1 /\ 1 будет 1; 0 /\ 1 будет 0; 1 /\ 0 будет 0) Получается: 11000000 При конъюнкции числа 00000000 с любым другим числом всегда будет 0. (Поэтому можно было и не переводить октеты 0 в двоичную систему)                                                             

1) Переводим каждый октет маски в двоичную систему счисления (010 = 000000002, 25510  = 111111112 - это надо запомнить)
25510 = 111111112 25510 = 111111112 22410 = 111000002 010 = 000000002
                                                            

любым другим числом всегда будет получаться тоже число. (Поэтому

можно было и не переводить октеты 255 в двоичную систему). Выполняем конъюнкцию маски с IP-адресом: 11100000 /\ 11010000 (всегда: 1 /\ 1 будет 1; 0 /\ 1 будет 0; 1 /\ 0 будет 0) Получается: 11000000 При конъюнкции числа 00000000 с любым другим числом всегда будет 0. (Поэтому можно было и не переводить октеты 0 в двоичную систему)                                                             

4) Получившиеся октеты переводим обратно в десятичную систему счисления.
64 и 128 так и остаются. Дальше идет 110000002 = 19210 194 так и остается. Получается 64.128.192.194
5) Ищем совпадения в таблице.
64 - B; 128 - C; 192 - D; 194 - E;                                               

Ответ: BCDE