Слайд 2
Высказывания - логические величины, логические константы
Высказывание (суждение) – это
повествовательное предложение, в
котором что-либо утверждается или
отрицается.
По поводу любого высказывания
можно сказать истинно оно или ложно.
Слайд 3
Какие из предложений являются высказываниями? Определите их истинность
1.
Число 6 – чётное.
Да
2. Посмотрите на доску.
Нет
3. Все роботы являются машинами.
Да
Слайд 4
4. У каждой лошади есть хвост.
Да
5. Внимание!
Нет
6. Кто отсутствует?
Нет
Какие из предложений являются высказываниями? Определите их истинность
Слайд 5
Придумайте одно истинное и одно
ложное высказывание
Слайд 6
Высказывания бывают общими, частными или единичными
Общее высказывание начинается
со слов: все, всякий, каждый, ни один
Частное высказывание начинается
со слов: некоторые, большинство, и т.п.
Во всех других случаях высказывания являются единичными
Слайд 7
Какие из приведённых высказываний являются общими?
Не все книги
содержат полезную информацию
Да
Кошка является домашним животным
Нет
Все солдаты храбрые
Да
Ни один
внимательный человек не совершит оплошность
Да
Слайд 8
Какие из приведённых высказываний являются частными?
Некоторые мои друзья
собирают марки
Да
Все лекарства неприятны на вкус
Нет
А – первая буква
в алфавите
Нет
Многие растения обладают целебными свойствами
Да
Слайд 9
Логические переменные, выражения, операции
Логическая переменная: символически обозначенная логическая
величина (А, В, Х, Y, …)
Логическое выражение –
простое или сложное высказывание
Слайд 10
Сложное высказывание строится из простых с помощью логических
операций (связок)
Операция отрицания (инверсия)
Присоединение «НЕ»к высказыванию
меняет его истинное значение
на
противоположное
Логическое отрицание обозначается: ,
или ~A
Слайд 11
Пример
Рассмотрим высказывание: “Неверно, что 4 делится на 3”.
Обозначим А = “Число 4
делится на 3”
Тогда логическая форма отрицания этого высказывания имеет вид: ~A
Слайд 12
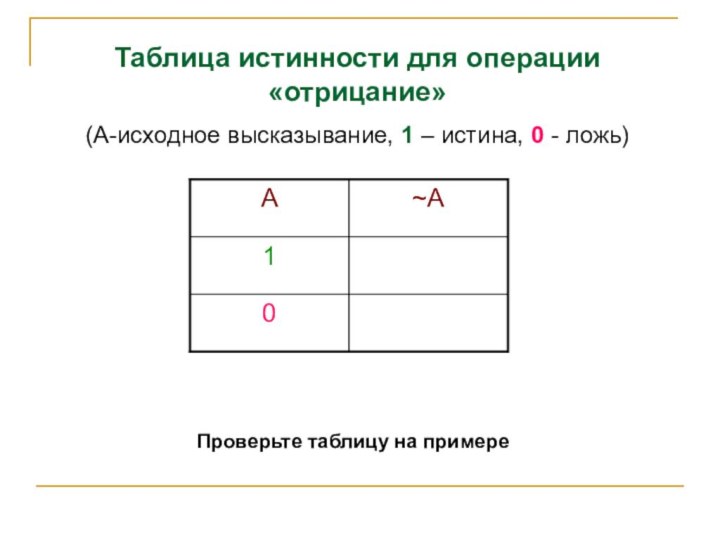
Проверьте таблицу на примере
Таблица истинности для операции «отрицание»
(А-исходное высказывание, 1 – истина, 0 - ложь)
Слайд 13
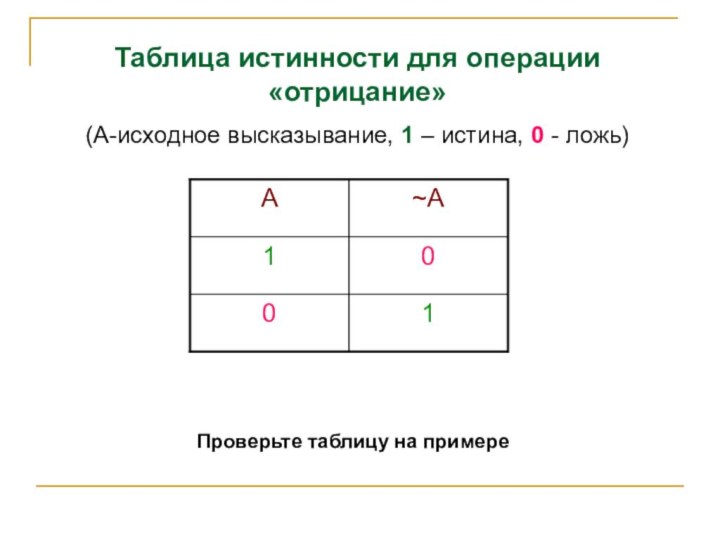
Проверьте таблицу на примере
Таблица истинности для операции «отрицание»
(А-исходное высказывание, 1 – истина, 0 - ложь)
Слайд 14
Операция логического умножения (конъюнкция)
Объединение высказываний
с помощью
логического «И».
Высказывание, полученное в
результате
конъюнкции, ложно тогда и
только тогда, когда ложно хотя бы одно из
входящих высказываний
Конъюнкция обозначается , & или ×
Слайд 15
Из двух простых высказываний постройте сложное и проверьте
на истинность, используя логическую связку И
Пример: А=«Марс -
планета» В=«Число 12 - чётное»
Придумайте и проверьте на истинность свой пример сложного высказывания используя логическую связку И
Слайд 16
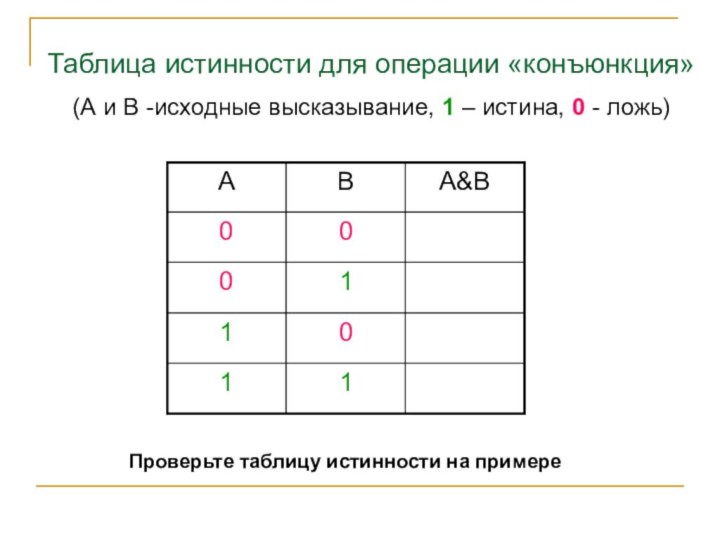
Таблица истинности для операции «конъюнкция»
(А и В
-исходные высказывание, 1 – истина, 0 - ложь)
Проверьте таблицу
истинности на примере
Слайд 17
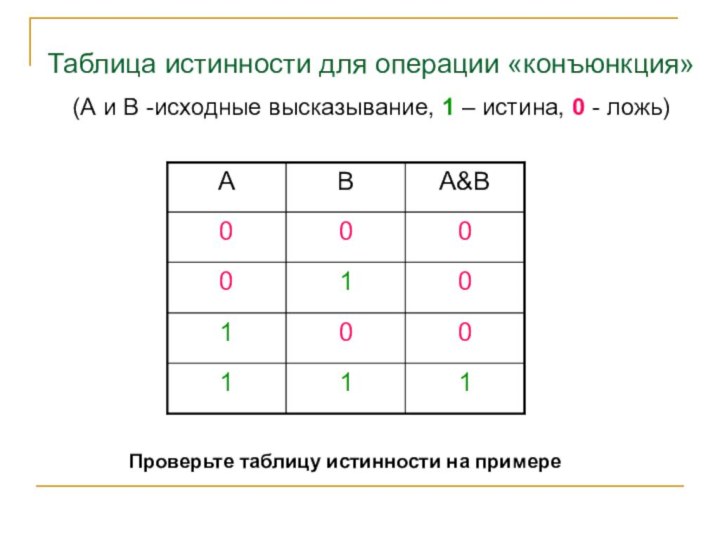
Таблица истинности для операции «конъюнкция»
(А и В
-исходные высказывание, 1 – истина, 0 - ложь)
Проверьте таблицу
истинности на примере
Слайд 18
Операция логического сложения (дизъюнкция)
Соединение высказываний с помощью
логического «или». Высказывание, полученное в результате дизъюнкции, истинно тогда
и только тогда, когда истинно хотя бы одно из исходных высказываний.
Дизъюнкция обозначается «V» или «+»
Слайд 19
Из двух простых высказываний постройте сложное и проверьте
на истинность, используя логическую связку ИЛИ
Пример:
А=«Земля вращается
вокруг Солнца» В=«Число 13 - чётное»
Придумайте и проверьте на истинность свой пример сложного высказывания используя логическую связку ИЛИ
Слайд 20
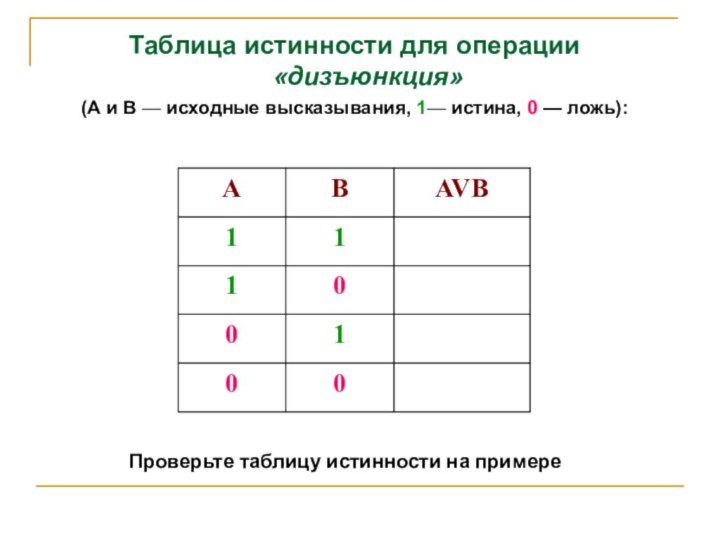
Таблица истинности для операции «дизъюнкция»
(А и В
— исходные высказывания, 1— истина, 0 — ложь):
Проверьте таблицу
истинности на примере
Слайд 21
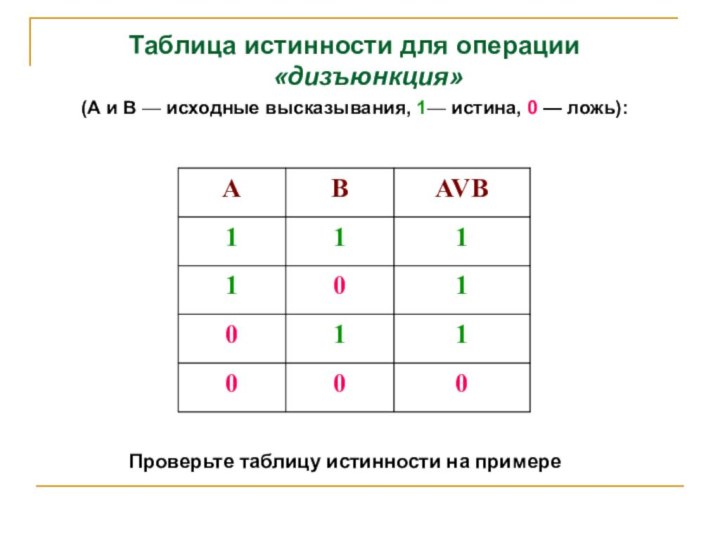
Таблица истинности для операции «дизъюнкция»
(А и В
— исходные высказывания, 1— истина, 0 — ложь):
Проверьте таблицу
истинности на примере
Слайд 22
Операция импликации
(следствие)
Позволяет получить сложное высказывание из двух простых
высказываний и грамматической конструкции «если..., то...».
Импликация ложна тогда и
только тогда, когда посылка истинна, а заключение - ложно. В остальных случаях импликация истинна.
Импликация обозначается знаками « » и « »
Слайд 23
Из двух простых высказываний постройте сложное и проверьте
на истинность, используя логическую связку ЕСЛИ…ТО
Пример: А=«выглянет Солнце»
В=«станет тепло»
Придумайте и проверьте на истинность свой пример сложного высказывания используя логическую связку ЕСЛИ…ТО
Слайд 24
Таблица истинности для операции«импликация»
(А и В —
исходные высказывания, 1 – истина, 0 — ложь):
Проверьте
таблицу истинности на примере
Слайд 25
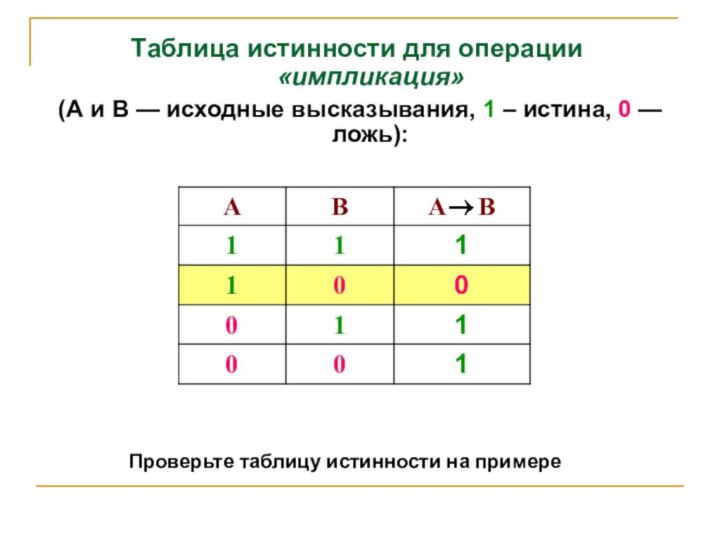
Таблица истинности для операции«импликация»
(А и В —
исходные высказывания, 1 – истина, 0 — ложь):
Проверьте
таблицу истинности на примере
Слайд 26
Операция эквивалентности (равносильность)
Полученное сложное высказывание содержит слова «тогда
и только тогда, когда»…
Эквивалентность истинна, если оба исходных
высказывания имеют одинаковые истинностные значения.
Эквивалентность обозначается знаком « »
или .
Слайд 27
Из двух простых высказываний постройте сложное и проверьте
на истинность, используя логическую связку ТОГДА И ТОЛЬКО ТОГДА…КОГДА
Пример: А=«треугольник прямоугольный»
В=«квадрат большей стороны равен сумме
квадратов других сторон»
Придумайте и проверьте на истинность свой пример сложного высказывания используя логическую связку ТОГДА И ТОЛЬКО ТОГДА…КОГДА
Слайд 28
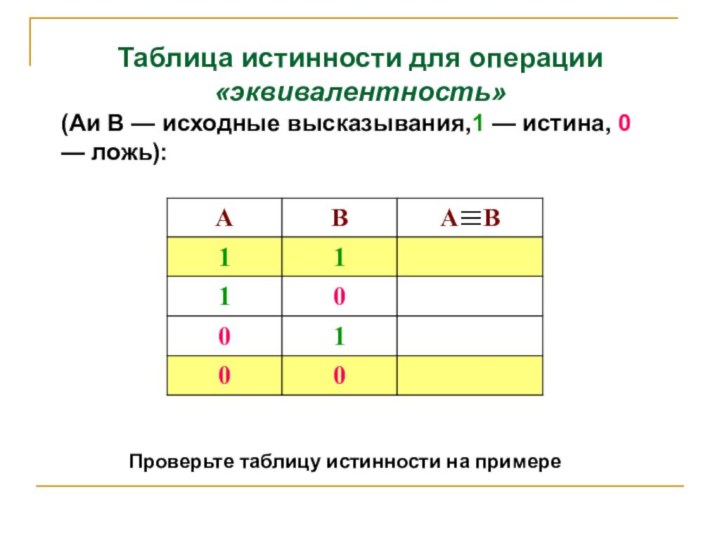
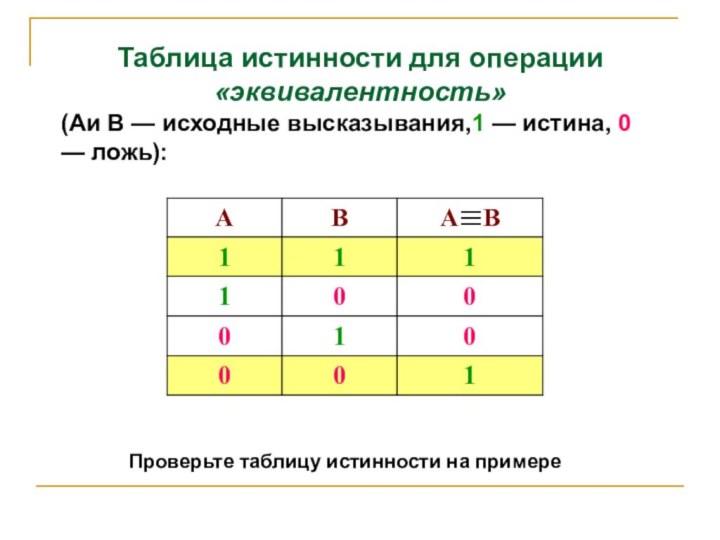
Таблица истинности для операции «эквивалентность»
(Аи В — исходные
высказывания,1 — истина, 0 — ложь):
Проверьте таблицу истинности на
примере
Слайд 29
Таблица истинности для операции «эквивалентность»
(Аи В — исходные
высказывания,1 — истина, 0 — ложь):
Проверьте таблицу истинности на
примере