Слайд 2
Линейная аппроксимация
При обработке экспериментальных данных часто возникает необходимость
аппроксимировать их линейной функцией.
Аппроксимацией (приближением) функции f(x) называется нахождение
такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.
В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.
Слайд 3
В случае если аппроксимация проводится на непрерывном множестве
точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой
аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.
Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.
Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.
Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).
Слайд 4
Аппроксимация линейной функцией
Любая линейная функция может быть записана
уравнением
Аппроксимация заключается в отыскании коэффициентов a и b уравнения
таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.
С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:
Слайд 5
Решение поставленной задачи сводится к нахождению экстремума указанной
функции двух переменных. С этой целью находим частные производные
функции функции по коэффициентам a и b и приравниваем их к нулю.
Слайд 6
Решаем полученную систему уравнений
Слайд 7
Определяем значения коэффициентов
Слайд 8
Для вычисления коэффициентов необходимо найти следующие составляющие:
Слайд 9
Тогда значения коэффициентов будут определены как
Слайд 10
Реализация
Для примера реализации воспользуемся набором значений, полученных в
соответствии с уравнением прямой
y = 8 · x -
3
Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
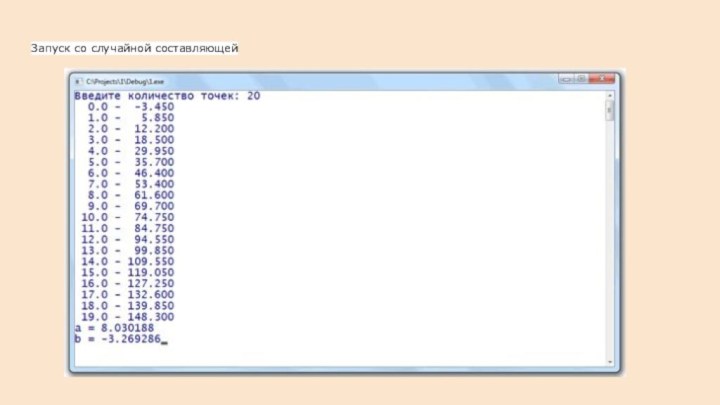
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.
Слайд 11
#include
#include
// Задание начального набора значений
double **
getData(int n) {
double **f;
f = new double*
[2];
f[0] = new double[n];
f[1] = new double[n];
for(int i=0; i f[0][i] = (double)i;
f[1][i] = 8*(double)i - 3;
// Добавление случайной составляющей
//f[1][i] = 8*(double)i - 3 + ((rand()%100)-50)*0.05;
}
return f;
}
Слайд 12
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double
*a, double *b, int n) {
double sumx =
0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
for(int i=0; i sumx += x[0][i];
sumy += x[1][i];
sumx2 += x[0][i]*x[0][i];
sumxy += x[0][i]*x[1][i];
}
*a = (n*sumxy - (sumx*sumy))/(n*sumx2-sumx*sumx);
*b = (sumy - *a*sumx)/n;
return;
}
int main() {
double **x, a, b;
int n;
system("chcp 1251");
system("cls");
printf("Введите количество точек: ");
scanf("%d",&n);
x = getData(n);
for(int i=0; i printf("%5.1lf - %7.3lf\n",x[0][i], x[1][i]);
getApprox(x, &a, &b, n);
printf("a = %lf\nb = %lf", a, b);
getchar(); getchar();
return 0;
}
Слайд 13
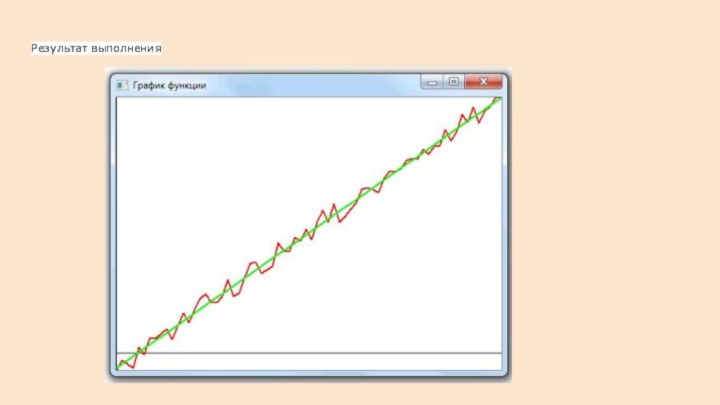
Результат выполнения
Запуск без случайной составляющей
Слайд 14
Запуск со случайной составляющей
Слайд 15
Построение графика функции
Для наглядности построим график функции, полученный
аппроксимацией по методу наименьших квадратов. Подробнее о построении графика
функции описано здесь.
#include
const int NUM=70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM,LPARAM);
double **x; // массив данных
// Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
for(int i=0; i sumx += m[0][i];
sumy += m[1][i];
sumx2 += m[0][i]*m[0][i];
sumxy += m[0][i]*m[1][i];
}
*a = (n*sumxy - (sumx*sumy))/(n*sumx2-sumx*sumx);
*b = (sumy - *a*sumx)/n;
return;
}
Слайд 16
// Задание исходных данных для графика
// (двумерный массив,
может содержать несколько рядов данных)
double ** getData(int n) {
double **f;
double a, b;
f = new double* [3];
f[0] = new double[n];
f[1] = new double[n];
f[2] = new double[n];
for(int i=0; i double x = (double)i * 0.1;
f[0][i] = x;
f[1][i] = 8*x - 3 + ((rand()%100)-50)*0.05;
}
Слайд 17
getApprox(f, &a, &b, n); // аппроксимация
for(int i=0;
i
a*x + b;
}
return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow=1) {
double OffsetY, OffsetX;
double MAX_X = 0;
double MAX_Y = 0;
double ScaleX, ScaleY;
double min, max;
int height, width;
int X,Y; // координаты в окне (в px)
HPEN hpen;
height = rectClient.bottom - rectClient.top;
width = rectClient.right - rectClient.left;
Слайд 18
// Область допустимых значений X
min = x[0][0];
max = x[0][0];
for(int i=0; i
min)
min = x[0][i];
if(x[0][i] > max)
max = x[0][i];
}
double temp = max - min;
MAX_X = max - min;
OffsetX = min*width/MAX_X; // смещение X
ScaleX = (double)width/MAX_X; // масштабный коэффициент X
Слайд 19
// Область допустимых значений Y
min =
x[1][0];
max = x[1][0];
for(int i=0; i
j=1; j<=numrow; j++) {
if(x[j][i] < min)
min = x[j][i];
if(x[j][i] > max)
max = x[j][i];
}
}
Слайд 20
MAX_Y = max - min;
OffsetY =

max*height/(MAX_Y); // смещение Y
ScaleY = (double)height/MAX_Y; // масштабный
коэффициент Y
// Отрисовка осей координат
hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
SelectObject(hdc, hpen);
MoveToEx(hdc,0,OffsetY,0); // перемещение в точку (0;OffsetY)
LineTo(hdc, width, OffsetY); // рисование горизонтальной оси
MoveToEx(hdc,OffsetX,0,0); // перемещение в точку (OffsetX;0)
LineTo(hdc, OffsetX, height); // рисование вертикальной оси
DeleteObject(hpen); // удаление черного пера
// Отрисовка графика функции
int color = 0xFF; // красное перо для первого ряда данных
for(int j=1; j<=numrow; j++) {
hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
SelectObject(hdc, hpen);
X = (int)(OffsetX + x[0][0]*ScaleX); // координаты начальной точки графика
Y = (int)(OffsetY - x[j][0]*ScaleY);
MoveToEx(hdc,X,Y,0); // перемещение в начальную точку
for(int i=0; i X = OffsetX + x[0][i]*ScaleX;
Y = OffsetY - x[j][i]*ScaleY;
LineTo(hdc, X, Y);
}
color = color << 8; // изменение цвета пера для следующего ряда
DeleteObject(hpen); // удаление текущего пера
}
Слайд 21
// Главная функция
int WINAPI WinMain (HINSTANCE hInstance,
HINSTANCE hPrevInstance,

LPSTR lpCmdLine, int nCmdShow) {
HWND hwnd;
MSG msg;
WNDCLASS w;
x = getData(NUM); // задание исходных данных
memset(&w,0,sizeof(WNDCLASS));
w.style = CS_HREDRAW | CS_VREDRAW;
w.lpfnWndProc = WndProc;
w.hInstance = hInstance;
w.hbrBackground=CreateSolidBrush(0x00FFFFFF);
w.lpszClassName = "My Class";
RegisterClass(&w);
hwnd = CreateWindow("My Class", "График функции",
WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
hInstance, NULL);
ShowWindow(hwnd,nCmdShow);
UpdateWindow(hwnd);
while(GetMessage(&msg, NULL, 0, 0)) {
TranslateMessage(&msg);
DispatchMessage(&msg);
}
return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
WPARAM wparam, LPARAM lparam) {
HDC hdc;
PAINTSTRUCT ps;
switch (Message) {
case WM_PAINT:
hdc = BeginPaint(hwnd, &ps);
DrawGraph(hdc,ps.rcPaint, x, NUM, 2); // построение графика
EndPaint(hwnd,&ps);
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
default:
return DefWindowProc(hwnd, Message, wparam, lparam);
}
return 0;
}
Слайд 23
https://www.youtube.com/watch?v=_-XAg8gQ2ak
Метод наименьших квадратов, урок 1/2. Линейная функция















![Презентация по теме: Линейная аппроксимация. // Область допустимых значений X min = x[0][0]; max = x[0][0]; for(int](/img/tmb/6/553128/7c011d82a7c5e290a7993f0077ef41be-720x.jpg)
![Презентация по теме: Линейная аппроксимация. // Область допустимых значений Y min = x[1][0]; max = x[1][0]; for(int i=0; i](/img/tmb/6/553128/c2774c7d27985d5f9f084a63c9d2f319-720x.jpg)