- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по информатике на тему Системы счисления
Содержание
- 2. Цель: закрепление и обобщение знаний учащихся по теме
- 3. оглавлениеОбщие сведения о системах счисленияСистемы счисления с
- 4. Система счисления – это знаковая система, в
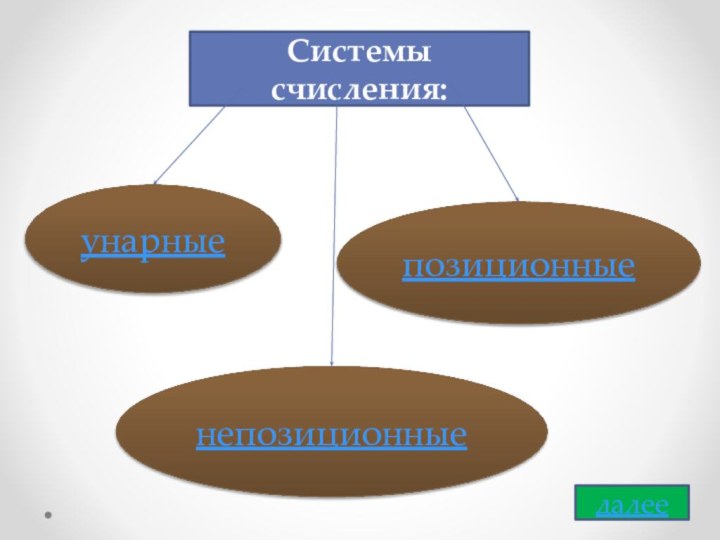
- 5. Системы счисления:унарныенепозиционныепозиционныедалее
- 6. Унарная система счисленияДля записи чисел используется всего один символ – палочка, узелок, зарубка, камушек и т.д.назад
- 7. Непозиционная система счисленияКоличественный эквивалент (количественное значение) цифры
- 8. Позиционная система счисленияКоличественный эквивалент цифры в числе
- 9. Формы записи числаСвернутая14351,1оглавление
- 10. Двоичной системой счисленияназывается позиционная система счисления с
- 11. Восьмеричной системой счисленияназывается позиционная система счисления с
- 12. Шестнадцатеричной системой счисленияназывается позиционная система счисления с
- 13. Правило перевода натурального числа системы счисления с
- 14. Правило перевода целого десятичного числа в число
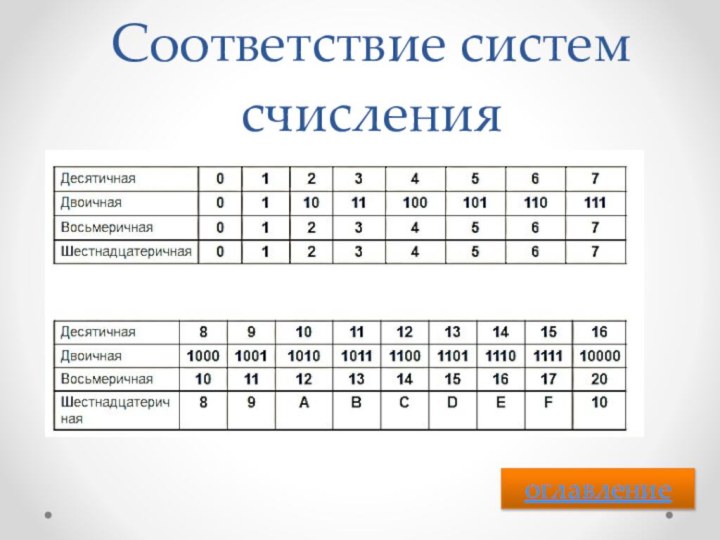
- 16. Соответствие систем счисленияоглавление
- 17. Сложение При сложении цифры суммируются по разрядам, и
- 19. Вычитание При вычитании из меньшей цифры большей
- 21. Умножение Если при умножении однозначных чисел возникает
- 23. Деление Деление в любой позиционной системе производится
- 24. Скачать презентацию
- 25. Похожие презентации
Цель: закрепление и обобщение знаний учащихся по теме «Системы счисления»подготовка к контролю по темеПроведение контроля по теме (в форме теста)



















Слайд 3
оглавление
Общие сведения о системах счисления
Системы счисления с разными
основаниями
Правила перевода из десятичной системы счисления в систему счисления
с другим основанием и наоборотАрифметические операции в позиционных системах счисления
Тренажер для подготовки к контролю
Контроль по теме
Используемая литература
Слайд 4 Система счисления – это знаковая система, в которой
приняты определенные правила записи чисел.
Знаки, при помощи которых
записываются числа, называются цифрами, а их совокупность – алфавитом системы счисления.Знаки, используемые для записи чисел в различных системах счисления
Слайд 6
Унарная система счисления
Для записи чисел используется всего один
символ – палочка, узелок, зарубка, камушек и т.д.
назад
Слайд 7
Непозиционная система счисления
Количественный эквивалент (количественное значение) цифры в
числе не зависит от ее положения в записи числа.
назад
Слайд 8
Позиционная система счисления
Количественный эквивалент цифры в числе зависит
от ее положения в записи числа.
Основание позиционной системы равно
количеству цифр, составляющих ее алфавит.назад
Слайд 10
Двоичной системой счисления
называется позиционная система счисления с основанием
2. Для записи чисел используются только две цифры: 0
и 1.Пример:
Слайд 11
Восьмеричной системой счисления
называется позиционная система счисления с основанием
8. Для записи чисел используются цифры: 0, 1, 2,
3, 4, 5, 6, 7.Пример:
Слайд 12
Шестнадцатеричной системой счисления
называется позиционная система счисления с основанием
16. Для записи чисел используются цифры: 0, 1, 2,
3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.Пример:
оглавление
Слайд 13 Правило перевода натурального числа системы счисления с основанием
q в целое десятичное число
Перейти к развернутой записи числа
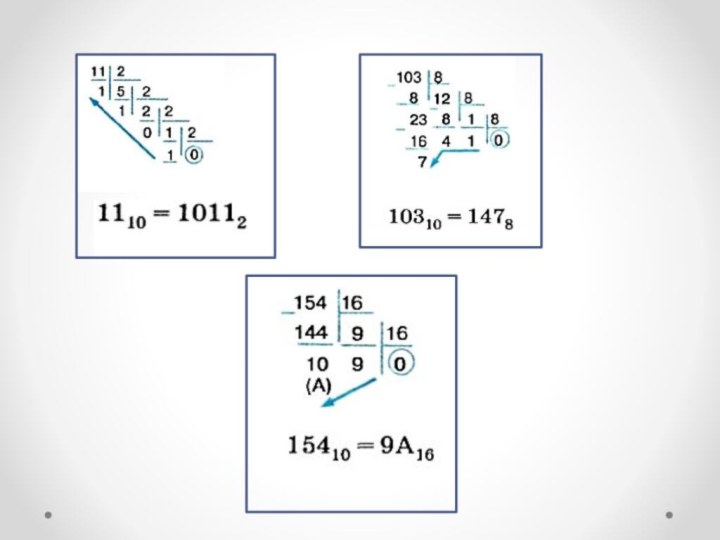
и вычислить его значениеСлайд 14 Правило перевода целого десятичного числа в число системы
счисления с
основанием q
Последовательно выполнять деление числа и получаемых
целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю.Полученные остатки привести в соответствие с алфавитом новой системы счисления.
Составить число, записывая его, начиная с последнего полученного остатка.
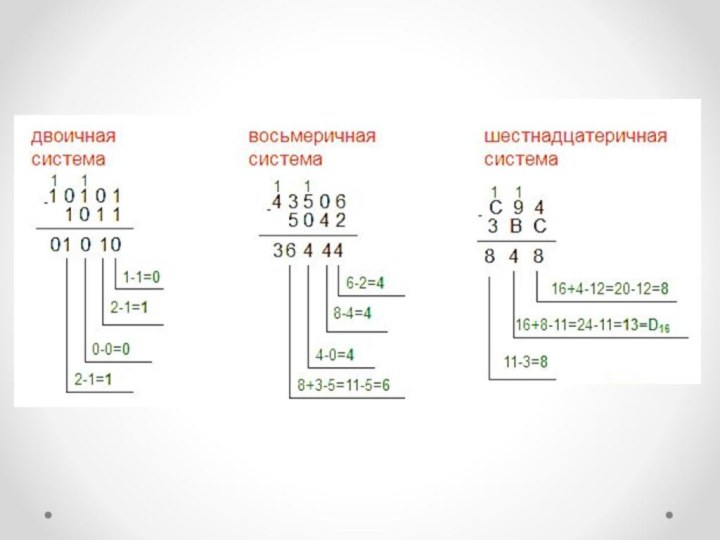
Слайд 17
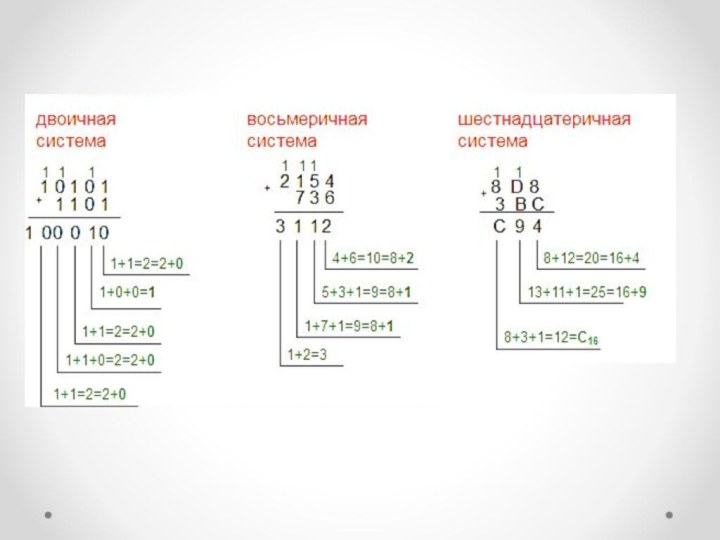
Сложение
При сложении цифры суммируются по разрядам, и если
при этом возникает переполнение разряда, то производится перенос в
старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления.
Слайд 19
Вычитание
При вычитании из меньшей цифры большей в
старшем разряде занимается единица, которая при переходе в младший
разряд будет равна основанию системы счисления
Слайд 21
Умножение
Если при умножении однозначных чисел возникает переполнение
разряда, то в старший разряд переносится число кратное основанию
системы счисления. При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления.
Слайд 23
Деление
Деление в любой позиционной системе производится по
тем же правилам, как и деление углом в десятичной
системе, то есть сводится к операциям умножения и вычитания.оглавление





























