Слайд 2
Информационное моделирование
Что такое информационное моделирование ?
Что такое моделирование.
Натурные
модели. Материальные модели – натурные модели. Модель воспроизводит только
те свойства оригинала, которые понадобятся человеку при ее использовании. Свойства модели зависят от цели моделирования.
============================================
Информационные модели. Для информатики они представляют наибольший интерес. Натурная модель – это физическое подобие. Информационная модель - это ее описание. Способы описания : словесное на естественном языке, математическое, графическое и др. Объект моделирования: материальный объект; явление природы; процесс. Моделирование – это деятельность человека по созданию модели (натурной или информационной).
===========================================
Слайд 3
Современным инструментом для информационного моделирования является компьютер.
Модель –
это упрощенное подобие реального объекта. Модель отражает лишь некоторые
свойства объекта, существенные для достижения цели моделирования.
========================================
Для сложных объектов в науке используется термин «система». Модель используется как заменитель реальной системы для воспроизведения отдельных ее функций, для прогноза ее поведения в определенных условиях.
==========================================
Формализация. Информационная модель описывает объект моделирования в форме каких-либо знаков: букв, цифр, картографических элементов, математических или химических формул и т.п.
Формализация есть результат перехода от реальных свойств объекта моделирования к их формальному обозначению в определенной знаковой системе.
Слайд 5
Основное преимущество компьютера перед человеком
Современным инструментом для информационного
моделирования является компьютер.
Современные суперЭВМ это многопроцессорные комплексы, которые
позволяют добиться очень высокой производительности и могут применяться для расчетов в реальном времени в метеорологии, военном деле , науке и т.п.
Главное преимущество компьютера перед человеком — способность к быстрому счету. Современные компьютеры считают со скоростями в сотни тысяч, миллионы и даже миллиарды операций в секунду!
Учитывая, что расчеты производятся над многозначными числами (10-20 десятичных цифр), вычислительные способности человека нельзя даже сравнивать с компьютерными. Эти феноменальные вычислительные возможности проявляются, прежде всего, в компьютерном математическом моделировании.
Слайд 6
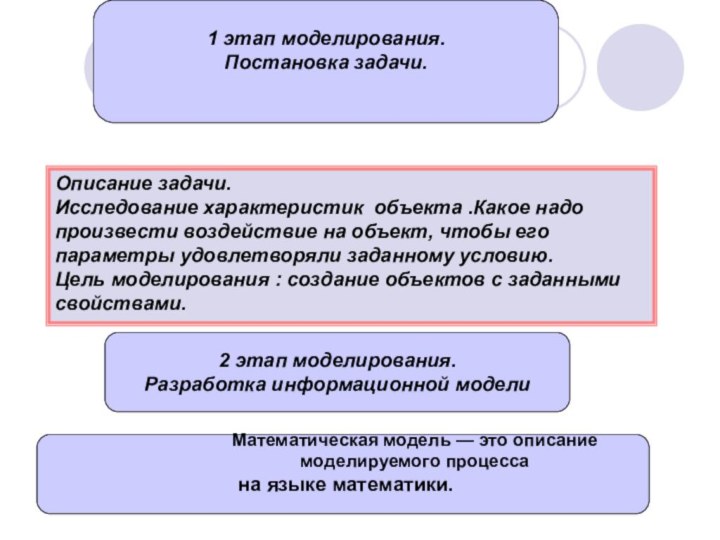
1 этап моделирования.
Постановка задачи.
2 этап моделирования.
Разработка информационной модели
Описание
задачи.
Исследование характеристик объекта .Какое надо произвести воздействие на объект,
чтобы его параметры удовлетворяли заданному условию.
Цель моделирования : создание объектов с заданными свойствами.
Математическая модель — это описание моделируемого процесса
на языке математики.
Слайд 7
Еще в XVIII-XIX веках ученые-математики начали изобретать методы
решения таких математических задач, которые не удавалось решить точно,
аналитически.
Например, вы знаете, что квадратное уравнение всегда можно решить точно, а вот кубическое — уже не всегда. Такие методы называются численными методами. Они сводят решение любой задачи к последовательности арифметических операций. Но эта цепочка арифметических вычислений может быть очень длинной. И чем точнее мы хотим получить решение, тем она длиннее.
Может оказаться так, что для решения сложной задачи численным методом ученому потребуется вся жизнь. А может и этого не хватить! Например, какой смысл начинать расчет прогноза погоды на завтрашний день, если для этого потребуется несколько лет работы?
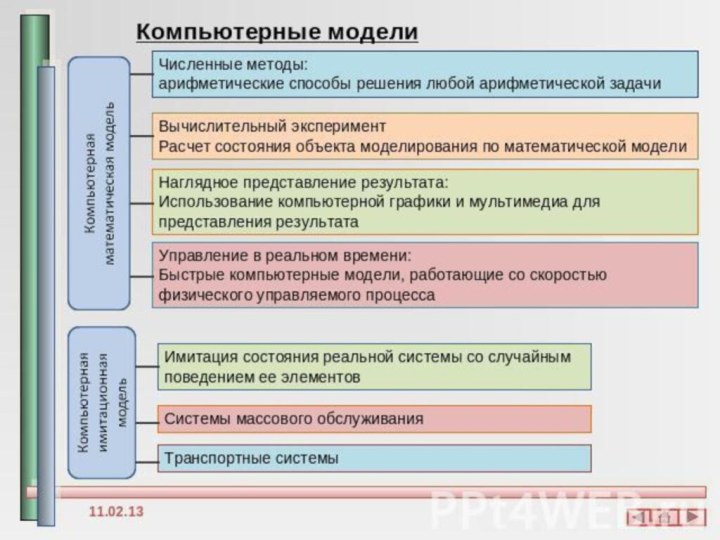
Компьютерная модель
Слайд 8
Компьютерная математическая модель
Появление компьютеров сняло эти проблемы. Стало
возможным проводить расчеты сложных математических моделей за приемлемое время.
Например, рассчитать погоду на завтрашний день до его наступления. Ученые перестали себя ограничивать в сложности создаваемых математических моделей, полагаясь на быстродействие компьютеров.
Компьютерная математическая модель — это программа, реализующая расчеты состояния моделируемой системы по ее математической модели. Пример математической
Модели.
Слайд 9
Системы неравенств с двумя переменными
Y
X2+y2=2
x
2x+3y=0
0
Рис.7
Множество решений данной
системы неравенств -- полукруг
Слайд 10
3 этап моделирования
Что такое вычислительный эксперимент?
Компьютерное моделирование —

основа представления знаний в ЭВМ. Прогресс моделирования связан с
разработкой систем компьютерного моделирования, а прогресс в информационной технологии — с актуализацией опыта моделирования на компьютере, с созданием банков моделей, методов и программных систем, позволяющих собирать новые модели из моделей банка
Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом. Говорят также: «численный эксперимент» .т. е. эксперимент, осуществляемый экспериментатором над
исследуемой системой или процессом с помощью орудия эксперимента — компьютера, компьютерной среды, тех-
нологии.
Вычислительный эксперимент становится новым инструментом, методом научного познания, новой технологией также из-за возрастающей необходимости перехода от исследования линейных математических моделей систем к исследованию сложных и нелинейных математических моделей систем (анализ которых гораздо сложнее).Вычислительный эксперимент позволяет находить новые законо-мерности, проверять гипотезы, визуализировать ход событий и т. д.
Слайд 11
Рассмотрим пример вычислительного физического эксперимента.
Момент инерции. В «Открытой физике»
(2.6, ч. 1) есть интересный вычислительный эксперимент по нахождению
момента инерции твёрдого тела на примере системы, состоящей из четырёх шаров, нанизанных на одну спицу. Можно изменять положение этих шаров на спице, а также выбирать положение оси вращения, проводя её как через центр спицы, так и через её концы. Для каждого расположения шаров учащиеся вычисляют с помощью теоремы Штейнера о параллельном переносе оси вращения значение момента инерции. Данные для расчётов сообщает учитель. После вычисления момента инерции данные вводятся в программу и проверяются результаты, полученные учащимися.[2]
Слайд 12
Вычислительный эксперимент в некоторых случаях может заменить реальный
физический эксперимент.
Впечатляющий пример использования такой возможности — прекращение испытаний
ядерного оружия, которые сопровождались значительным экологическим ущербом. Благодаря очень точным математическим моделям и мощным компьютерам стало возможно просчитать все последствия, к которым приводит изменение в конструкции ядерной бомбы. Образно говоря, удалось «взорвать бомбу» внутри компьютера, ничего не разрушив.
Слайд 13
Визуализация результатов расчета
Важным свойством компьютерных математических моделей является
возможность визуализации результатов расчетов. Этим целям служит использование компьютерной
графики.
Представление результатов в наглядном виде — важнейшее условие для их лучшего понимания. Например, результаты расчетов распределения температуры в некотором объекте представляются в виде его разноцветного изображения: участки с самой высокой температурой окрашиваются в красный цвет, а в самой холодной — в синий. Участки с промежуточными значениями температуры окрашиваются в цвета спектра, равномерно переходящие от красного к синему (рис.2.7).
Слайд 15
Компьютерная графика
Компьютерная графика позволяет человеку в процессе проведения
численного эксперимента «заглянуть» в недоступные места исследуемого объекта. Можно
получить изображение любого сечения объекта сложной формы с отображением рассчитываемых характеристик: температурных полей, давления и пр. В реальном физическом эксперименте такое можно сделать далеко не всегда. Например, невозможно выполнить измерения внутри работающей доменной печи или внутри звезды. А на модели это сделать можно Пример компьютерной графики
Слайд 19
Управление на основе моделей
Еще одно важное направление компьютерного
математического моделирования связано с использованием компьютеров в управлении.
Компьютеры
используют для управления работой химических реакторов на заводах, атомных реакторов на электростанциях, ускорителей элементарных частиц в физических лабораториях, полета автоматических космических станций и т. д.
Управляя производственной или лабораторной установкой, компьютер должен просчитывать ее характеристики для того, чтобы вовремя снять показания с датчиков или оказать управляющее воздействие: включить реле, открыть клапан и т. п.
Все расчеты производятся по заложенным в программу управления математическим моделям. Важно, чтобы результаты этих расчетов получались в режиме реального времени управляемого процесса.
Слайд 20
Имитационное моделирование
Имитационное моделирование — особая разновидность моделирования на
компьютере.
Имитационная модель воспроизводит поведение сложной системы, элементы которой могут
вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.
Такое поведение в математике называется стохастический. Из курса физики вам знакомо явление броуновского движения: хаотического перемещения легких частиц на поверхности жидкости из-за неравномерных ударов молекул с разных сторон. Нельзя точно рассчитать траекторию броуновской частицы, но ее можно сымитировать на экране компьютера. Отсюда и происходит название — имитационная модель.
Слайд 21
Имитационное моделирование
К имитационным моделям относятся модели систем массового
обслуживания: например, системы торговли, автосервиса, скорой помощи, в которых
появление заявок на обслуживание и длительность обслуживания одной заявки — события случайные.
Задачи, решаемые с помощью имитационных моделей систем массового обслуживания, заключаются в поиске режимов работы служб сервиса (магазинов, авто-заправок и пр.), уменьшающих время ожидания клиентов.
Еще одним популярным объектом для имитационного моделирования являются транспортные системы: сеть городских дорог, перекрестки, светофоры, автомобили.
Слайд 22
Еще одним популярным объектом для имитационного моделирования являются
транспортные системы: сеть городских дорог, перекрестки, светофоры, автомобили.
Модель
имитирует движение транспортных потоков по городским улицам (рис. 2.8). Эксперименты на такой модели позволяют найти режимы управления движением (работа светофоров), уменьшающие возможность возникновения пробок. Работа имитационной модели всегда визуализируется на экране компьютера.
Слайд 24
Анализ результатов моделирования
Этап 4. Анализ результатов моделирования.
Конечная цель моделирования

— принятие решения, которое должно быть выработано на основе
всестороннего анализа полученных результатов. Этот этап решающий — либо вы продолжаете исследование, либо заканчиваете. Возможно, вам известен ожидаемый результат, тогда необходимо сравнить полученный и ожидаемый результаты. В случае совпадения вы сможете принять решение.
Основой для выработки решения служат результаты тестирования и экспериментов. Если результаты не соответствуют целям поставленной задачи, значит, допущены ошибки на предыдущих этапах. Это может быть либо слишком упрощенное построение информационной модели, либо неудачный выбор метода или среды моделирования, либо нарушение технологических приемов при построении модели. Если такие ошибки выявлены, то требуется корректировка модели, т. е. возврат к одному из предыдущих этапов. Процесс повторяется до тех пор, пока результаты эксперимента не будут отвечать целям моделирования. Главное, надо всегда помнить: выявленная ошибка — тоже результат. Как говорит народная мудрость, на ошибках учатся.
Слайд 25
Помимо специальных программ для создания компьютерных моделей в

исследовании используют инструменты прогнозирования— программные продукты, имеющие функции расчёта
прогнозов. Прогнозирование— один из важнейших видов деятельности человека на сегодняшний день. Ещё в древние времена прогнозы позволяли людям рассчитывать периоды засух, даты солнечных и лунных затмений и многих других явлений. С появлением вычислительной техники прогнозирование получило мощнейший толчок развития. Одним из первых применений вычислительных машин был расчёт баллистической траектории снарядов, то есть, фактически, прогноз точки падения снаряда на землю. Такой вид прогноза называется статическим прогнозом. Существуют две основные категории прогнозов: статические и динамические. Ключевое отличие состоит в том что динамические прогнозы предоставляют информацию о поведении исследуемого объекта на протяжении какого-либо значительного интервала времени. В свою очередь, статические прогнозы отражают состояние исследуемого объекта лишь в единственный момент времени и, как правило, в таких прогнозах фактор времени, в котором объект претерпевает изменения, играет незначительную роль. На сегодняшний день существует большое количество инструментов, позволяющих строить прогнозы. Все они могут быть подвергнуты классификации по многим признакам.
Слайд 26
Коротко о главном
Компьютерная математическая модель — это программа,
реализующая расчеты состояния моделируемой системы по ее математической модели.
Высокое быстродействие компьютеров позволяет быстро решать достаточно сложные математические задачи в процессе моделирования.
Вычислительный эксперимент — использование компьютерной математической модели для исследования поведения моделируемой системы.
Компьютерное управление техническими устройствами происходит в процессе расчетов по математическим моделям в режиме реального времени.
Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом.
Слайд 27
Вопросы и задания
1. Что общего и в
чем различие понятий «математическая модель» и «компьютерная математическая модель»?
2.
Расчет прогноза погоды на современном компьютере с быстродействием 1 млн операций в секунду длится в течение 1 часа. Оцените, сколько времени понадобилось бы для этого человеку, имеющему в своем распоряжении арифмометр (механический калькулятор)?
3. В чем состоит особенность компьютерного математического моделирования в процессе управления техническим устройством?
Слайд 28
4. Самолет находится на высоте 5000 метров. Обнаружилась
неисправность работы двигателя. Самолет начал падать. Бортовой компьютер производит
диагностику неисправности и сообщает пилоту о необходимых действиях. Для решения этой задачи ему нужно выполнить 108 вычислительных операций. Быстродействие компьютера — 1 млн оп/сек. Успеет ли летчик спасти самолет, если минимальная высота, на которой самолет можно вывести из пике, — 2000 метров?
5. В каких ситуациях используется имитационное моделирование?
6. Придумайте по одному примеру формы использования компьютерной графики для вычислительного эксперимента, для компьютерного управления и для имитационной модели.
Чему вы должны научиться, изучив главу 2 учебника.
• Строить табличные информационные модели по словесному описанию объектов и их свойств.
Слайд 29
Литература:
1.Информатика.ФГОС.8 класс.И.Г Семакин,Л.А. Залогова и др.
2.Компьютерный физический эксперимент
Л.
В. ПИГАЛИЦЫН,
< LEVP@RAMBLER.RU >, WWW.LEVPI.NAROD.RU, МОУ СОШ № 2, Г. ДЗЕРЖИНСК, НИЖЕГОРОДСКАЯ ОБЛ.