- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Перевод чисел в позиционных системах счисления
Содержание
- 2. Цель:Расширить и углубить знания о переводе чисел в позиционных системах счисления
- 3. Задачи:Образовательные:актуализация знаний по теме «Системы счисления»;дифференциация материала,
- 4. Планируемые результаты:Предметные: научиться переводить числа между системами
- 5. План урокаПеревод чисел из десятичной системы счисления
- 6. Ей было тысяча сто лет, Она в
- 7. Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления
- 8. Правила перевода целой части числаПоследовательно делить данное
- 9. Пример. Переведем число 15310 в 2-ую,
- 10. Правила перевода дробной части числаПоследовательно умножать дробную
- 11. Пример. Переведем число 0,6562510 в 2-ую, 8-ую
- 12. Перевод чисел в десятичную систему счисления.Правила.Разложить
- 13. Число 345,810 можно записать как:345,810 =300 +
- 14. В восьмеричной системе счисления:751, 258=7*82 +5*81 +
- 15. Перевод чисел из двоичной системы счисления
- 16. Перевод из 2-ой с.с. в 8-ю с.с.
- 17. Перевод из 2-ой с.с. в 16-ую
- 18. Решение задач по теме «Системы счисления» (подготовка
- 19. Задание 1 Сколько единиц в двоичной записи
- 20. Задание 2. Даны 4 числа, они записаны
- 21. 2) Для второго варианта воспользуемся связью между
- 22. Задание 3 Дано: а=D716 и b=331.
- 23. Задание 5 Решите уравнение: 608 + x
- 24. Задание 6 В системе счисления с некоторым
- 25. Задание 7. В саду 100q фруктовых деревьев,
- 26. Задание 8. Укажите, сколько всего раз
- 27. Задания для самостоятельного решенияВ саду 100 фруктовых
- 28. 6. Как записывается число 5678 в двоичной
- 29. 11. Какое из чисел является наименьшим? 1)
- 30. Скачать презентацию
- 31. Похожие презентации





























Слайд 3
Задачи:
Образовательные:
актуализация знаний по теме «Системы счисления»;
дифференциация материала, изученного
по теме «Системы счисления»;
стимулирование интереса к изучаемой теме;
Развивающие:
развитие навыков
индивидуальной практической деятельности;развитие коммуникационной компетентности у учащихся;
развитие мышления учащихся при решении логических задач;
Воспитательные:
повышение мотивации учащихся путем использования нестандартных задач;
формирование творческого подхода к решению задач, четкости и организованности, умения оценивать свою деятельность и деятельность своих товарищей;
воспитание духа здорового соперничества, дружелюбного отношения друг к другу, чувства коллективизма;
формирование навыков самоорганизации и инициативы.
Слайд 4
Планируемые результаты:
Предметные: научиться переводить числа между системами счислений
и пользоваться правилами перевода при решении заданий повышенной сложности
Метапредметные:
Регулятивные:
- Уметь самостоятельно контролировать своё время и управлять им.
- Адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение, как в конце действия, так и по ходу его реализации.
Личностные: - Формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию. - Формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики.
Познавательные:
- Поиск и выделение необходимой информации; применение методов информационного поиска, в том числе с помощью компьютерных средств.
Коммуникативные: - Формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности. - Устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор. - Осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;
Слайд 5
План урока
Перевод чисел из десятичной системы счисления в
двоичную, восьмеричную и шестнадцатеричную системы счисления
Перевод чисел в десятичную
систему счисления.Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления и обратно
Решение задач по теме «Системы счисления»
Задания для самостоятельного решения
Список используемой литературы
Слайд 6 Ей было тысяча сто лет, Она в сто первый
класс ходила, С собою по сто книг носила — Всё это
правда, а не бред!Когда, пыля десятком ног, Она шагала по дороге, За ней всегда бежал щенок С одним хвостом, зато — стоногий!
Она ловила каждый звук Своими десятью ушами, И десять загорелых рук Портфель и поводок держали.
И десять темно-синих глаз Рассматривали мир привычно… С такой девчонкой необычной И вы встречались, и не раз!
А.Стариков «Странная девочка»
Приём, использованный автором в стихотворении, современным школьникам, знающим, что для представления информации при компьютерной обработке данных используется двоичная система счисления, конечно же, понятен: число 2 (количество рук, например) в двоичном представлении отображается числом 10, число 4 (количество ног у щенка) — числом 100 и т.д. Но, если учесть, что стихотворение было написано 30 лет назад, когда ещё не было персональных компьютеров, и ни о какой массовой компьютеризации и информатизации общества речь не шла, такое стихотворение могло показаться сложным для понимания».
Слайд 7 Перевод чисел из десятичной системы счисления в двоичную,
восьмеричную и шестнадцатеричную
системы счисления
Слайд 8
Правила перевода целой части числа
Последовательно делить данное число
на основание новой системы счисления (на 2, 8, 16),
до тех пор пока частное не станет равным нулю.Полученные остатки привести в соответствие с алфавитом шестнадцатеричной системы счисления.
Записать число в новой системе счисления, начиная с последнего остатка.
Слайд 9 Пример. Переведем число 15310 в 2-ую, 8-ую и
16-ую с.с.
153|2
152 76|2
1 76 38|2
0 38 19|20 18 9|2
1 8 4|2
1 4 2|2
0 2 1|2
0 0 0
1
частное
15310 = 100110012
153|8
152 19|8
1 16 2|8
3 0 0
2
частное
153|16
144 9|16
9 0 0
9
частное
15310 = 1328
15310 = 9916
Слайд 10
Правила перевода дробной части числа
Последовательно умножать дробную часть
числа на основание новой системы счисления (на 2, 8,
16), до тех пор пока дробная часть не станет равным нулю или до той точности, которая определена условием.Полученные остатки привести в соответствие с алфавитом шестнадцатеричной системы счисления.
Записать число в новой системе счисления, начиная с целой части первого произведения.
Слайд 11 Пример. Переведем число 0,6562510 в 2-ую, 8-ую и
16-ую с.с.
0, 65625х
21, 31250х
2
0, 62500х
2
1, 25000х
2
0, 50000х
2
1, 00000
0,6562510 = 0,101012
0, 65625х
8
5, 25000х
8
2, 00000
0, 65625х
16
+3, 93750
6 5625
10, 50000х
16
8, 00000
0,6562510 = 0,528
0,6562510 = 0,А816
А
Слайд 12
Перевод чисел в десятичную
систему счисления.
Правила.
Разложить число в
виде степенного ряда.
Подсчитать сумму произведений.
Разберем на примере в десятичной
системе счисления:
Слайд 13
Число 345,810 можно записать как:
345,810 =300 + 40
+ 5 + 0,8= 3*100+ 4*10 + 5+0,8
т.е.
345,810=3*102 +
4*101 +5*100 +8*10-1 Точно также число в степенной ряд можно разложить в любой системе счисления:
В двоичной системе счисления:
1110, 012=1*23 + 1*22 +1*21 + 1*20 + 0*2-1 + 1*2-2 =
= 8+4+2+0,25=14,2510
3 2 1 0 -1-2
показатели степеней
Слайд 14
В восьмеричной системе счисления:
751, 258=7*82 +5*81 + 1*80
+ 2*8-1 + 5*8-2 =
= 7*64+40+1+2/8+5/64=489,3310
В шестнадцатеричной системе
счисления:8Е5, А816= 8*162 +14*161 + 5*160 + 10*16-1 + + 8*16-2 =
= 2048+224+5+10/16+8/256=2277,6562510
2 1 0 -1-2
показатели степеней
2 1 0 -1-2
показатели степеней
Слайд 15 Перевод чисел из двоичной системы счисления в восьмеричную
и шестнадцатеричную
системы счисления
и обратно
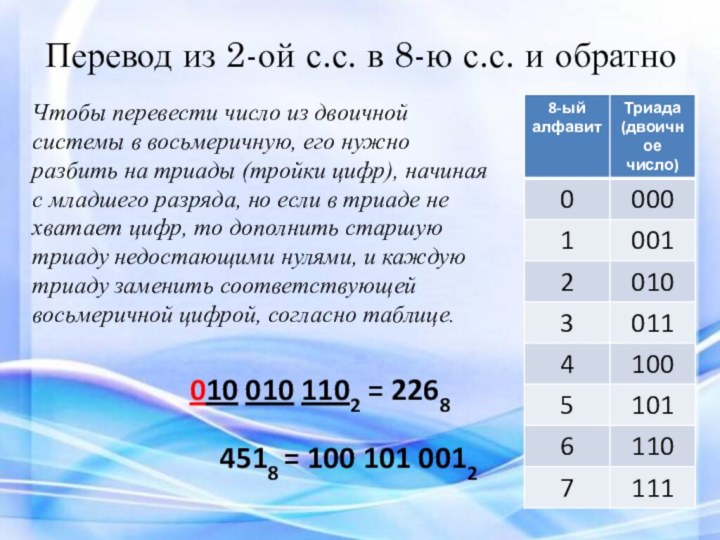
Слайд 16 Перевод из 2-ой с.с. в 8-ю с.с. и
обратно
010 010 1102 = 2268
Чтобы перевести число из
двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, но если в триаде не хватает цифр, то дополнить старшую триаду недостающими нулями, и каждую триаду заменить соответствующей восьмеричной цифрой, согласно таблице.4518 = 100 101 0012
Слайд 17 Перевод из 2-ой с.с. в 16-ую с.с. и
обратно
Чтобы перевести число из двоичной системы в шестнадцатеричную, его
нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, но если в тетраде не хватает цифр, то дополнить старшую тетраду недостающими нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой, согласно таблице.0010 0100 11102 = 24Е16
А7F116 = 1010 0111 1111 00012
Слайд 18
Решение задач по теме «Системы счисления»
(подготовка к ЕГЭ)
В
ЕГЭ встречается примерно 8 различных типов задач на системы
счисления.Слайд 19 Задание 1 Сколько единиц в двоичной записи десятичного числа
149?
Решение:
Переведем данное число в двоичную систему счисления и
подсчитаем единицы.149|2
148 74|2
1 74 37|2
0 36 18|2
1 18 9|2
0 8 4|2
1 4 2|2
0 2 1|2
0 0 0
1
Ответ: 4 единицы
Слайд 20 Задание 2. Даны 4 числа, они записаны с использованием
различных систем счисления. Укажите среди этих чисел то, в
двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них. 1) 6310 * 410 2) F816 + 110 3) 3338 4) 111001112Решение:
Нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее и чисел, в которых ровно 6 единиц.
252|2
252 126|2
0 126 63|2
0 62 31|2
1 30 15|2
1 14 7|2
1 6 3|2
1 2 1|2
1 0 0
1
1) В первом варианте перемножим числа и переведем их в двоичную систему счисления:
6310 * 410 = 25210 = 111111002
В 1 варианте содержится 6 единиц
Слайд 21 2) Для второго варианта воспользуемся связью между шестнадцатеричной
и двоичной системами счисления: каждую цифру шестнадцатеричного числа можно
переводить отдельно в тетраду :F816 + 110 = 1111 1000 +1 = 111110012
Во 2 варианте содержится 6 единиц
3) Для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду двоичных цифр:
3338 = 110110112
В 3 варианте содержится 6 единиц
4) 111001112
В 4 варианте содержится 6 единиц
Теперь сравним все 4 числа и выберем большее из них:
1) 111111002
2) 111110012
3) 110110112
4) 111001112
Таким образом, все 4 числа, указанные в вариантах ответов содержат ровно 6 единиц, но наибольшее из них – первое
Слайд 22 Задание 3 Дано: а=D716 и b=331. Какое из чисел
с, записанных в двоичной системе счисления, удовлетворяет неравенству a
< c < b?Решение:
Надо перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить. Рассмотрим один из вариантов, переведем в 8-ю с.с.
D716 = 011 010 1112= 3278
011 011 0012 = 3318
011 011 1002 = 3348
011 010 1112 = 3278
011 011 0002 = 3308
Таким образом, в восьмеричной системе между числами 3278 и 3318 может быть только 3308
Ответ: 4
Слайд 23 Задание 5 Решите уравнение: 608 + x = 1207 Ответ
запишите в шестеричной системе счисления. Основание системы счисления указывать
не нужно.Решение:
Удобнее всего перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему:
608 = 6*81+0*80=4810
1207 =1*72+2*71+0*80=49+14=6310
уравнение приобретает вид , 48+х=63, откуда получаем х = 15
переводим 15 в шестеричную систему счисления:
Ответ: 23.
15|6
12 2|6
3 0 0
2
Слайд 24 Задание 6 В системе счисления с некоторым основанием десятичное
число 49 записывается в виде 100. Укажите это основание.
Решение
100х=4910
1*х2+0*х1+0*х0=49
х2=49;
х1=-7; х2=7Основание системы счисления положительно, значит х=7
Ответ : 1007=4910
Слайд 25 Задание 7. В саду 100q фруктовых деревьев, из них
33q яблони, 33q груши, 16q слив и 5q вишен.
В какой системе счисления посчитаны деревья?Решение:
Представим каждое из чисел в виде степенного ряда
100q=q2
33q=3q+3
22q=2q+2
16q=q+6
5q=5
Ответ : q=8
q2 = 3q+3+2q+2+q+6+5
q2 = 6q+16
q2-6q-16=0
q1=-2; q2=8
Основание системы счисления положительно, значит q=8.
Слайд 26 Задание 8. Укажите, сколько всего раз встречается цифра
2 в записи чисел 10, 11, 12, …, 17
в системе счисления с основанием 5.Решение:
Запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 5:
10 = 205, 17 = 325 .
Заметим, что оба они содержат цифру 2, так что, 2 цифры мы уже нашли
Между 205 и 325 есть еще числа
215, 225, 235, 245, 305, 315.
В них 5 цифр 2 (в числе 225 – сразу две двойки), поэтому всего цифра 2 встречается 7 раз
Таким образом, верный ответ – 7.
Слайд 27
Задания для самостоятельного решения
В саду 100 фруктовых деревьев
– 14 яблонь и 42 груши. Найдите основание системы
счисления, в которой указаны эти числа.Десятичное число 57 в некоторой системе счисления записывается как «212». Определите основание системы счисления.
Десятичное число 109 в некоторой системе счисления записывается как «214». Определите основание системы счисления.
Решите уравнение . Ответ запишите в четверичной системе счисления. Основание системы счисления указывать не нужно.
Решите уравнение . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Слайд 28 6. Как записывается число 5678 в двоичной системе
счисления?
1) 10111012 2) 1001101112 3) 1011101112 4) 111101112
7. Как записывается
число A8716 в восьмеричной системе счисления?1) 4358 2) 15778 3) 52078 4) 64008
8. Как записывается число 7548 в шестнадцатеричной системе счисления?
1) 73816 2) 1A416 3) 1EC16 4) A5616
9. Дано: a=EA16 и b=3548, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству a
10. Дано: a=E716 и b=3518. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству a
Слайд 29
11. Какое из чисел является наименьшим?
1) E616
2) 3478 3) 111001012 4) 232
12.Какое из чисел является
наибольшим? 1) 9B16 2) 2348 3) 100110102 4) 153
13. Сколько единиц в двоичной записи десятичного числа 513?
1) 5 2) 2 3) 3 4) 4
14. Сколько нулей в двоичной записи десятичного числа 497?
1) 5 2) 2 3) 3 4) 4
15. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) 3110 * 810 + 110 2) F016 + 110 3) 3518 4) 111000112
16. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 4 единицы. Если таких чисел несколько, укажите наибольшее из них.
1) 1510 * 1610 + 410 2) D716 + 110 3) 3448 4) 111000012





























