Слайд 2
Содержание.
Что такое алгоритм?
Свойства алгоритма.
Форма записи алгоритмов.
Слайд 3
Что такое алгоритм?
Человек ежедневно встречается с необходимостью следовать

тем или иным правилам, выполнять различные инструкции и указания.
Например, переходя через дорогу на перекрестке без светофора надо сначала посмотреть направо. Если машин нет, то перейти полдороги, а если машины есть, ждать, пока они пройдут, затем перейти полдороги. После этого посмотреть налево и, если машин нет, то перейти дорогу до конца, а если машины есть, ждать, пока они пройдут, а затем перейти дорогу до конца.
В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует получить и какие действия и в каком порядке следует для этого выполнить. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.
Слайд 4
Алгоpитм — заранее заданное понятное и точное предписание
возможному исполнителю совершить определенную последовательность действий для получения решения
задачи за конечное число шагов.
Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в 783—850 гг.
Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в 783—850 гг.
Слайд 5
Свойства алгоритма.
Основные свойства алгоритмов следующие:
1. Понятность для
исполнителя — исполнитель алгоритма должен понимать, как его выполнять.
Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.
2. Дискpетность (прерывность, раздельность) — алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов).
3.Опpеделенность — каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче.
Слайд 6
4. Pезультативность (или конечность) состоит в том, что
за конечное число шагов алгоpитм либо должен пpиводить к
pешению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.
5. Массовость означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма.
Слайд 7
Форма записи алгоритма.
На практике наиболее распространены следующие формы
представления алгоритмов:
словесная (запись на естественном языке);
графическая (изображения из графических символов);
псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
программная (тексты на языках программирования).
Слайд 8
Словесное описание алгоритма.
Словесный способ записи алгоритмов представляет собой
описание последовательных этапов обработки данных. Алгоритм задается в произвольном
изложении на естественном языке
Словесный способ не имеет широкого распространения, так как такие описания:
Строго не формализуемы: страдают многословностью записей;
допускают неоднозначность толкования отдельных предписаний.
Слайд 9
Например. Записать алгоритм нахождения наибольшего общего делителя
(НОД)
двух натуральных чисел (алгоритм Эвклида).
Алгоритм может быть следующим:
задать два числа;
если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
определить большее из чисел;
заменить большее из чисел разностью большего и меньшего из чисел;
повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи.
Слайд 10
Графическое описание алгоритма.
Графический способ представления алгоритмов является более
компактным и наглядным по сравнению со словесным.
При графическом
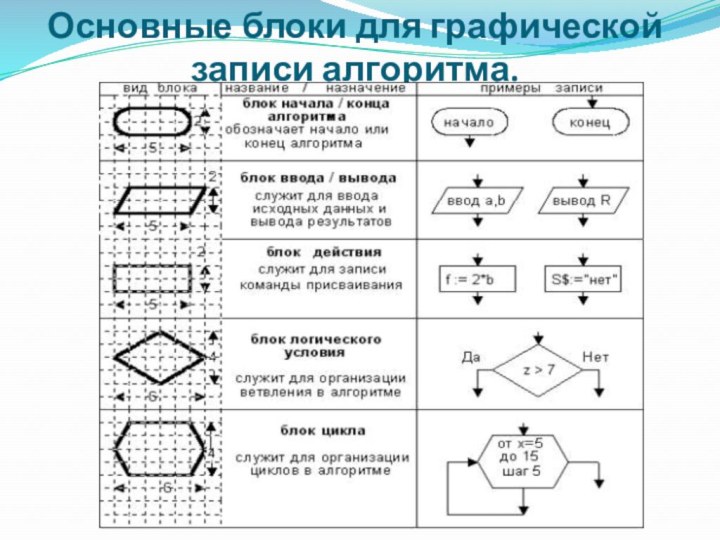
представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.