Презентация на тему Логические основы

принимать переменные?
Сколько различных значений могут принимать логические переменные?

«Истина» (1)

«Ложь» (0)

буквами.

А – «Два умножить на два равно четырем».
В –

Какова истинность высказываний?

Первое высказывание истинно (А = 1).
Второе высказывание ложно (В = 0).

связок и, или, не,
которые в алгебре логики заменяются

в одно с помощью союза «и» называется
операцией логического

Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

1) «2 × 2 = 5 и 3 × 3 = 10» (ложно)
2) «2 × 2 = 5 и 3 × 3 = 9» (ложно)
3) «2 × 2 = 4 и 3 × 3 = 10» (ложно)
4) «2 × 2 = 4 и 3 × 3 = 9» (истинно)

операцию логического умножения (конъюнкцию) принято обозначать значком «&» (амперсенд)

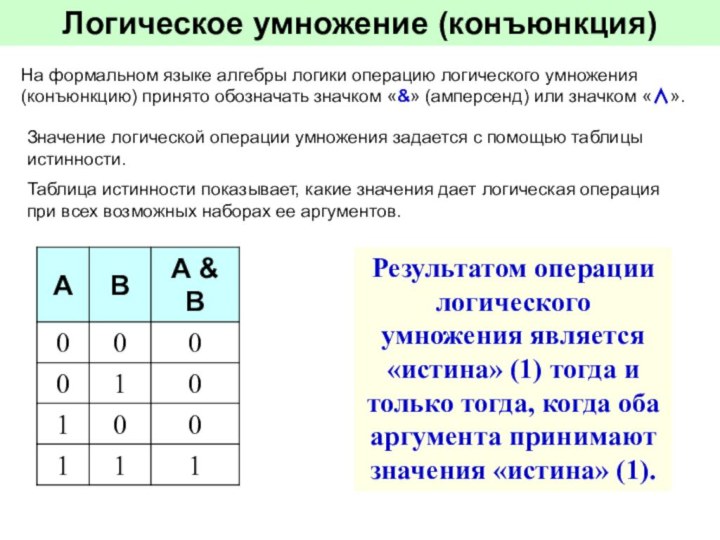
Значение логической операции умножения задается с помощью таблицы истинности.
Таблица истинности показывает, какие значения дает логическая операция при всех возможных наборах ее аргументов.

Результатом операции логического умножения является «истина» (1) тогда и только тогда, когда оба аргумента принимают значения «истина» (1).

в одно с помощью союза «или» называется
операцией логического

Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

1) «2 × 2 = 5 или 3 × 3 = 10» (ложно)
2) «2 × 2 = 5 или 3 × 3 = 9» (истинно)
3) «2 × 2 = 4 или 3 × 3 = 10» (истинно)
4) «2 × 2 = 4 или 3 × 3 = 9» (истинно)

операцию логического операцию логического сложения (дизъюнкцию) принято обозначать значком

Значение логической операции сложения задается с помощью таблицы истинности.

Результатом операции логического сложения является «ложь» (0) тогда и только тогда, когда оба аргумента принимают значения «ложь» (0).

называется операцией логического отрицания или инверсией.
Логическое отрицание (инверсия)

Высказывание «Два умножить на два равно четырем» истинно.
Высказывание, образованное с помощью операции логического отрицания, «Два умножить на два не равно четырем» ложно.

операцию логического отрицания (инверсию) над логическим высказыванием А принято

Значение логической операции отрицания задается с помощью таблицы истинности.

Результатом операции логического отрицания является «истина» (1), когда аргумент принимает значение «ложь» (0), и значение «ложь» (0), когда аргумент принимает значение «истина» (1).

«истина»?
2) Когда результатом операции логического сложения (дизъюнкции) является