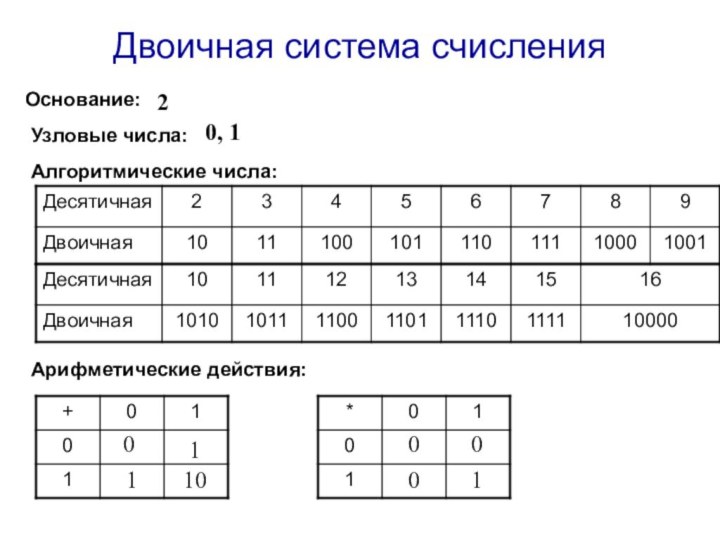
и обозначения чисел.
О2. Символы, которые служат для обозначения
однозначных чисел, из которых строятся остальные числа системы счисления, называются узловыми, все остальные числа системы, построенные из узловых называются алгоритмическимиО3. Система счисления, в которой алгоритмические числа образуются сложением узловых, называется аддитивной.
О4. Система счисления, в которой алгоритмические числа образуются сложением и умножением узловых, называется аддитивно-мультипликативной.
О5. Система счисления называется непозиционной, если каждый числовой знак в записи любого числа в ней имеет одно и то же значение независимо от его расположения в числе. Если значение числового знака зависит от его расположения в записи числа, то система называется позиционной.