Слайд 2
Тема урока: Решение треугольников с использованием электронных таблиц
Цели
урока:
совершенствовать знания и умения учащихся по темам: «Соотношения между
сторонами и углами треугольника», «Использование математических функций в электронных таблицах»;
развивать вычислительную культуру учащихся, в том числе с использованием математических таблиц В.М. Брадиса, электронных таблиц Calc;
воспитывать у учащихся чувства товарищества, взаимовыручки;
способствовать формированию у них навыков самооценки.
Оборудование:
компьютеры с установленной операционной системой Linux;
мультимедийный проектор;
четырехзначные математические таблицы В.М.Брадиса;
презентации, выполненные учащимися;
чертежные принадлежности;
памятки
Слайд 3
План урока
I. Организационный момент.
II. Актуализация знаний.
III. Решение задач.
IV.
Итог урока.
Ход урока
Учитель математики. Ребята, мы завершили с вами
изучение темы, которую в Древней Греции считали введением в практику астрономических наблюдений. Вообще слово «тригонометрия» буквально означает «измерение треугольников»( от греч. «тригонон» - треугольник, «метрио» - измеряю. Сегодня на уроке мы будем иметь возможность закрепить знания и умения по теме «Решение треугольников». Но смоделируем различные ситуации:
у вас под рукой есть компьютер;
вы можете воспользоваться лишь математическими таблицами;
вы оказались на необитаемом острове, и у вас кроме песка на берегу океана и ветки, сломанной с дерева, больше ничего нет.
Интеграция [ лат. Integratio – восстановление, восполнение,
integer – целый], объединение в целое каких-либо частей, элементов.
Современный словарь
иностранных слов
Слайд 4
Учитель информатики. Именно поэтому девизом сегодняшнего урока мы
выбрали слова американского писателя К.Н.Боуви ( высказывание записано на
доске):
«Немногие умы гибнут от износа,
по большей части они ржавеют от неупотребления».
Учитель математики. Для того, чтобы успешно решать задачи в течение всего урока, вспомним с вами определения и формулировки теорем, отражающие соотношения между сторонами и углами в треугольнике.
Вопросы и задания учащимся.
Дать определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.
Сформулировать теорему синусов и теорему косинусов.
Вычислить 5,342 (с помощью таблиц Брадиса (сообщение учащихся), с помощью электронных таблиц (сообщение учащихся), умножением в столбик).
Вычислить , используя таблицы Брадиса, электронные таблицы и алгоритм извлечения квадратного корня из числа (демонстрация алгоритма учащимися)
Найти синус 45°19´(с помощью таблиц Брадиса, с помощью электронных таблиц (сообщение учащихся).
Слайд 5
Учитель информатики. А сейчас, ребята, вы будете решать
геометрические задачи. При выполнении вычислений можете использовать электронные таблицы
и/или таблицы Брадиса, так как вы сидите за компьютером вдвоем. А для самопроверки вычислений не забывайте о том, что вы умеете возводить в степень, умножать, делить, извлекать квадратный корень без всяких подручных средств. Если какой-то алгоритм действий забудете, то вы можете обратиться к памяткам, которые у вас лежат на столе (памятки 1-3).
Слайд 6
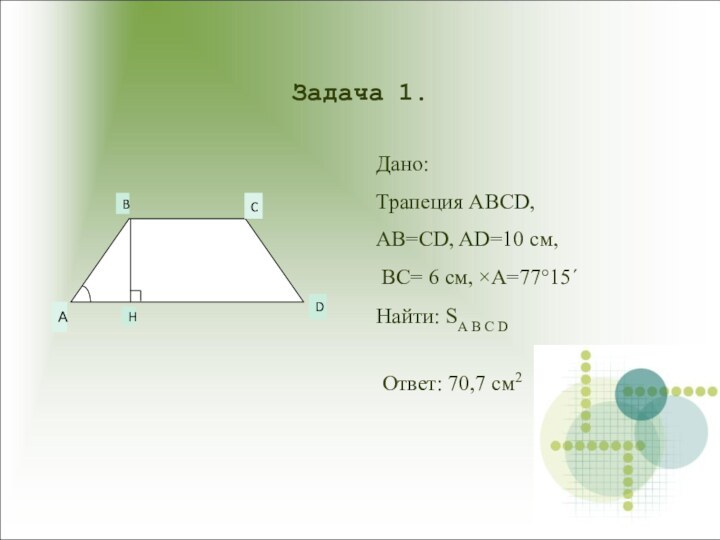
Задача 1.
Дано:
Трапеция ABCD,
AB=CD, AD=10 см,
BC= 6 см,
×A=77°15´
Найти: SA B C D
Ответ: 70,7 см2
Слайд 7
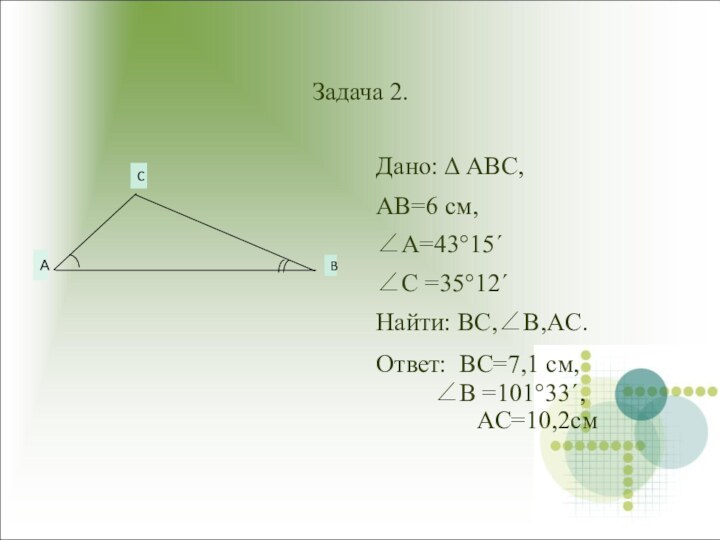
Задача 2.
Дано: ABC,
AB=6 см,
A=43°15´
C =35°12´
Hайти: BC,B,AC.
Ответ: BC=7,1
см,
B =101°33´,
AC=10,2см
Слайд 8
Самооценка
На мой взгляд, сегодня на уроке я заслужил
оценку
«5»
«2»
«3»
«4»
Слайд 9
Резюме. Мне кажется, что для получения хороших результатов
в учебе или в работе
достаточно иметь под рукой нужную
книгу
одно другого не исключает, а скорее дополняет
необходим только компьютер
Слайд 10
Учитель математики. Сегодня на уроке вы услышали
о том, как вычисляли квадратный корень, находили значения синусов
углов в те времена, когда не было ни таблиц, ни компьютеров, и сами попробовали производить некоторые из этих вычислений без вспомогательных средств.
Учитель информатики. Нам кажется, что высказывание Ж. Лагранжа подводит итог нашему уроку:
«Нужно стремиться узнать путь, часто непрямой и трудный, которым шли первые изобретатели. . . чтобы понять, сколь многим мы обязаны этим истинным благодетелям человечества».
Слайд 11
Краткие сведения из истории математики и информатики
(сообщения учащихся
по ходу урока)
Слайд 12
Брадис
Владимир Модестович — советский математик — педагог,
член-корреспондент АПН.
Дата рождения: 23 декабря 1890
Место рождения: Псков
Дата смерти:
23 мая 1975(84 года)
Страна: СССР
Научная сфера: математика
Награды: медаль К.Д.Ушинского
Слайд 13
Брадис Владимир Модестович родился 23 декабря 1890 года

в городе Пскове. Окончил Петроградский университет, профессор, доктор педагогических
наук. В 1920―59 г.г. работал в Тверском институте народного образования. С 1959, после ухода на пенсию, руководил аспирантами, в 1965―71 г.г. был профессором -консультантом. Его основные труды посвящены теоретической и методической разработке вопросов повышения вычислительной культуры учащихся средней школы. В 1921 впервые вышли его "Таблицы четырехзначных логарифмов и натуральных тригонометрических величин". По известности это творение В.М.Брадиса было сравнимо с теоремой Пифагора. «Таблицы Брадиса» оказались в свое время таким же усилителем интеллекта, каким сейчас мы почитаем компьютер.
Заслуга В.М.Брадиса состояла в том, что он придумал способ, позволяющий до минимума сократить утомительные расчеты. Кропотливых расчетов В.М.Брадису предстояло проделать много, но они экономили массу времени всем последующим пользователям его таблиц. Эти таблицы стали советским бестселлером. С 1930-х годов их издавали едва ли не ежегодно и издают и в настоящее время.
назад
Слайд 14
Linux, произносится «линукс» — общее название операционных систем
на основе одноимённого ядра и собранных для него библиотек
и системных программ, разработанных в рамках проекта GNU.
В отличие от коммерческих систем, таких как Microsoft Windows или Mac OS X, Linux не имеет географического центра разработки. Нет и организации, которая владела бы этой системой; нет даже единого координационного центра. Программы для Linux — результат работы тысяч проектов.
Но Linux является полноценной многофункциональной операционной системой. Некоторые возможности этой системы мы сегодня научимся использовать.
назад
Операционная система Linux.
Линус Торвальдс — создатель ядра «Linux»

а л и в - с и н у
с
Страх и ужас наводили на людей солнечные и лунные затмения. В них видели дурные предзнаменования. Чтобы избежать совпадений какого-либо важного события с затмениями, необходимо было уметь их предсказывать, а для этого определять положение светил на небосводе в зависимости от времени года и суток. Поэтому и были созданы таблицы хорд окружностей (134 г. до н.э.) - таблицы, отражающие зависимость хорд от дуг, которые они стягивают (или от соответствующих центральных углов).
Древнегреческие ученые не знали наших тригонометрических функций, вместо синуса они пользовались хордой, равной удвоенной линии синуса половинной дуги. Заметим, что греческое слово «хорде», от которого происходит наш термин «хорда», буквально означает «тетива лука», а на арабском языке перевод близкий по смыслу звучит — залив, изгиб. Уже на латынь его так и перевели — «синус» — изгиб, залив.
Хорда лишь коэффициентом отличается от синуса половины дуги
AB=2Rsin(α/2) (рис.). Таким образом, таблицы хорд представляли собой, по существу, таблицы синусов.
назад
Рис.
Слайд 16
Памятка 1. Использование таблиц Брадиса при нахождении значений
тригонометрических функций
Помните главное:
при нахождении значений синуса или тангенса
угла пользоваться нумерацией градусов слева , а нумерацией минут - сверху;
при нахождении значений косинуса или котангенса угла пользоваться нумерацией градусов справа , а нумерацией минут - снизу;
если для получения значений тригонометрических функций углов понадобятся поправки, не забывайте, что синус и тангенс в первой четверти возрастают, а косинус и котангенс - убывают.
Слайд 17
Памятка 2. Извлечение квадратного корня
Рассмотрим два примера. Пусть
надо извлечь квадратный корень из чисел 6118,99 и 86616.Поступать
будем следующим образом.
Разобьём данное число на группы по две цифры в каждой, считая от запятой влево. В самой левой грани могут оказаться одна или две цифры.
Подберём число, квадрат которого является ближайшим к одной (7² =49<61) или двум (29²=841<866) цифрам левой грани, запишем его справа от знака равенства, квадрат этого числа запишем ниже числа, из которого извлекается корень, вычтем это квадрат (как при деление чисел).
Слайд 18
Памятка 2(продолжение). Извлечение квадратного корня
Число, записанное справа от
знака равенства, удвоим и запишем слева от разности (7×2=14
и 29×2=58.
Припишем теперь к этому произведению такую цифру ( её же припишем и к уже записанным цифрам корня), чтобы произведения ( 148×8=1184 и 584×4=2336) были возможно ближе к записанной ранее разности – это снова напоминает обычное деление.
Будем продолжать этот процесс, пока не достигнем необходимой вам точности.
Слайд 19
Памятка 3. Использование электронных таблиц при нахождении значений
математических функций
Помните главное:
при нахождении значений математических функций используются
следующие команды:
SQRT — вычисление квадратного корня;
POWER — вычисление аb, где а — основание степени,
b — показатель степени;
SIN — вычисляет синус угла;
COS — вычисляет косинус числа;
TAN — вычисляет тангенс угла;
RADIANS — преобразует градусы в радианы.
при нахождении значений синуса, косинуса, тангенса и котангенса значение угла должно быть представлено в радианах;
например для нахождения косинуса 36°17´ следует ввести следующую формулу: COS(RADIANS(36+17/60))
назад