- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по элективному курсу Математические основы информатики по теме Представление целых чисел. Прямой код. Дополнительный код
Содержание
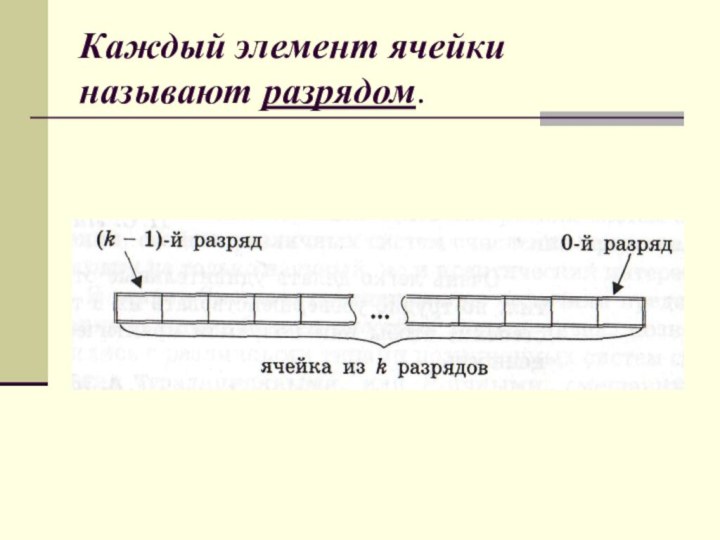
- 2. Каждый элемент ячейки называют разрядом.
- 3. Виды информации: числовая текстовая звуковая графическая
- 4. Задача перевода информации естественного происхождения в компьютерную называется задачей дискретизации и квантования
- 5. Представление целых чисел Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью
- 6. Способы представления целых чиселБеззнаковое для неотрицательных целых чисел Знаковый вид для отрицательных чисел
- 7. При беззнаковом представлении все разряды ячейки отводятся под само число
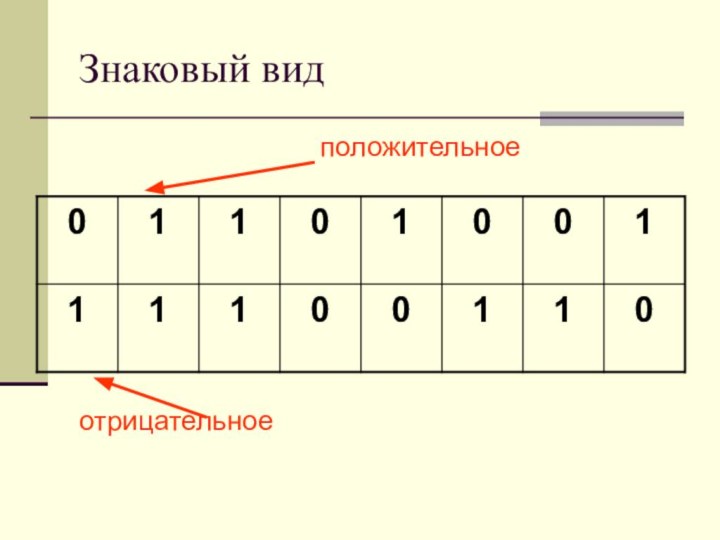
- 8. Знаковый вид
- 9. 1 байт (8 знаков)Беззнаковый – от 0 до 255Знаковый – от 0 до 127
- 11. Представление числа в привычной для человека форме
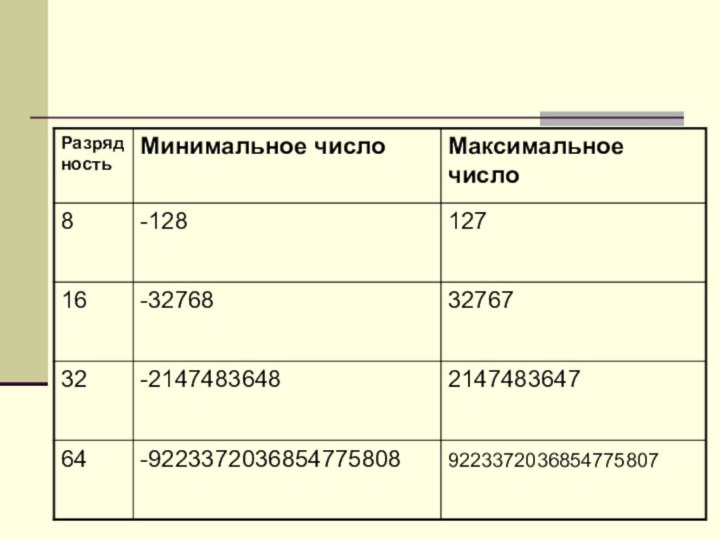
- 12. Задание Определите максимальное положительное число в восьмиразрядном и шестнадцатиразрядном знаковых способах представления чисел.
- 13. Пример 1 Число 53 = 1101012 в
- 14. Пример 2 Для числа 200 = 110010002
- 15. В k-разрядной целочисленной компьютерной арифметике 2k ≡ 0
- 16. k-разрядный дополнительный код отрицательного числа т —
- 17. Алгоритм получения дополнительного k-разрядного кода отрицательного
- 18. ЗадачаПолучим дополнительный код числа -52 для восьми- и шестнадцатиразрядной ячеек.
- 19. ЗадачаПостройте дополнительный восьмиразрядный код для чисел -128, -127 и -0
- 20. Восстановление модуля исходного десятичного отрицательного числа по
- 22. Скачать презентацию
- 23. Похожие презентации
Каждый элемент ячейки называют разрядом.


















Слайд 4
Задача перевода информации естественного происхождения в компьютерную называется
задачей дискретизации и квантования
Слайд 5
Представление целых чисел
Любое целое число можно рассматривать как
вещественное, но с нулевой дробной частью
Слайд 6
Способы представления
целых чисел
Беззнаковое для неотрицательных целых чисел
Знаковый вид для отрицательных чисел
Слайд 11 Представление числа в привычной для человека форме «знак-величина»,
при которой старший разряд ячейки отводится под знак, остальные
k - 1 разрядов — под цифры числа, называется прямым кодом.2k-1 - 1
Слайд 12
Задание
Определите максимальное положительное число в восьмиразрядном и
шестнадцатиразрядном знаковых способах представления чисел.
Слайд 13
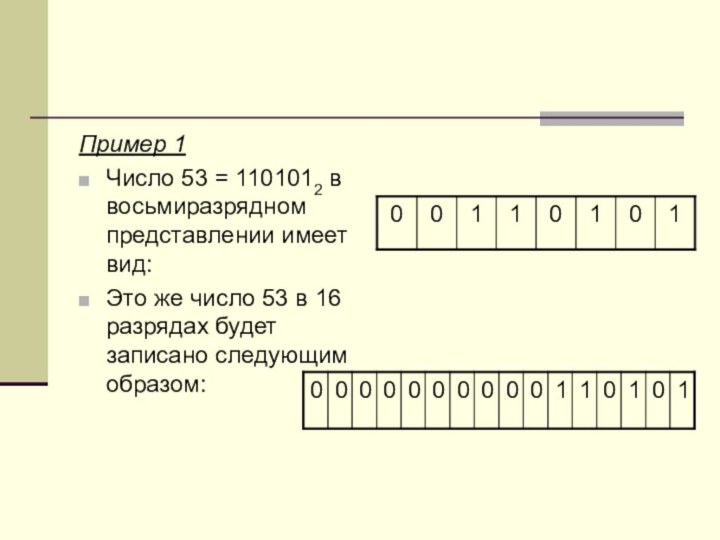
Пример 1
Число 53 = 1101012 в восьмиразрядном
представлении имеет вид:
Это же число 53 в 16 разрядах
будет записано следующим образом:
Слайд 14
Пример 2
Для числа 200 = 110010002 представление
в 8 разрядах со знаком невозможно, так как максимальное
допустимое число в таком представлении равно 127, а в беззнаковом восьмиразрядном представлении оно имеет вид:Слайд 16 k-разрядный дополнительный код отрицательного числа т — это
запись в k разрядах положительного числа 2к - |m|,
где |m| — модуль отрицательного числа m, |m| ≤ 2к-1(2k - |m|) + |m| = 2k≡0
Слайд 17
Алгоритм получения дополнительного
k-разрядного кода отрицательного числа
1. Модуль
числа представить прямым кодом в k двоичных разрядах.
2. Значения
всех разрядов инвертировать (все нули заменить на единицы, а единицы — на нули), получив, таким образом, k-разрядный обратный код исходного числа.3. К полученному обратному коду, трактуемому как k-разрядное неотрицательное двоичное число, прибавить единицу.
Слайд 20 Восстановление модуля исходного десятичного отрицательного числа по его
дополнительному коду
Способ 1 (обратная цепочка преобразований): вычесть единицу
из дополнительного кода, инвертировать полученный код и перевести полученное двоичное представление числа в десятичное.Способ 2: по приведенному выше алгоритму построить дополнительный код для имеющегося дополнительного кода искомого числа и представить результат в десятичной системе счисления.





























