- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы счисления
Содержание
- 2. План работы:
- 3. Системой счисления - называется совокупность символов (цифр) и правил их использования для представления чисел.
- 4. Позиционные и непозиционные системы счисленияВ позиционных
- 5. Наиболее употребляемыми в настоящее время позиционными системами
- 6. Римская система в которой в качестве цифр
- 7. Запись числа в позиционной системе счисления: Любое
- 8. Перевод любого числа в десятичную систему счисления:
- 9. В чем же преимущество у шестнадцатеричной системы
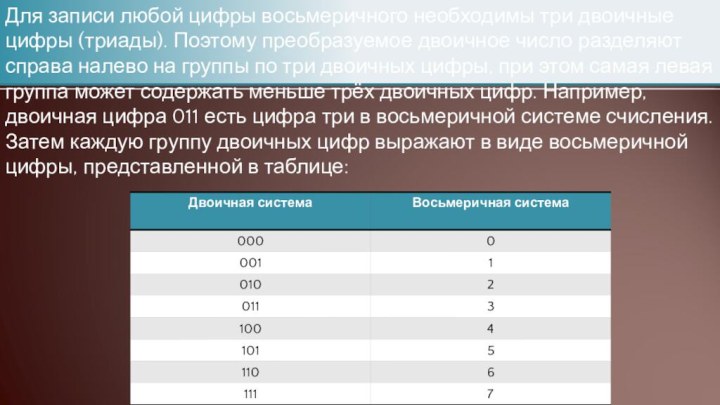
- 10. Для записи любой цифры восьмеричного необходимы три
- 11. Задание 1. Переведите число 1011012 в десятичную систему счисления.Решение.1011012=1*25+0*24+1*23+1*22+0*21+1*20=32+8+4+1=4510Ответ: 1011012=4510
- 12. Задача 2.Перевести десятичное число в двоичную СС117(10)Ответ: 1110101(2)
- 13. Скачать презентацию
- 14. Похожие презентации
План работы:












Слайд 3
Системой счисления -
называется совокупность символов (цифр) и
правил их использования для представления чисел.
Слайд 4
Позиционные и непозиционные
системы счисления
В позиционных системах счисления
один и тот же числовой знак (цифра) в записи
числа имеет различные значения в зависимости от того места (разряда), где он расположен.В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Слайд 5
Наиболее употребляемыми в настоящее время позиционными системами являются:
2
— двоичная (в дискретной математике, информатике, программировании);
3 — троичная;
8
— восьмеричная;10 — десятичная (используется повсеместно);
12 — двенадцатеричная (счёт дюжинами);
13 — тринадцатеричная;
16 — шестнадцатеричная (используется в программировании, информатике);
60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.
Слайд 6 Римская система в которой в качестве цифр используются
некоторые буквы:
I(1), V(5), X(10), L(50), C(100), D(500), M(1000).
Примеры
непозиционной системы счисления:
В системе значение цифры не зависит от ее положения в числе. Например, в числе ХХХ цифра Х встречается трижды, а в каждом случае обозначает одну и туже величину 10, а в сумме ХХХ это 30.
Слайд 7
Запись числа в позиционной системе счисления:
Любое число
в позиционной системе счисления с произвольным основанием можно записать
в виде многочленаА (s)=ansn+an-1sn-1+ …+a-ms-m,
где s - основание системы, а степень соответствует разряду цифры а в числе А(s)
Например: 54510=5•102+4•101+ 5•100
Слайд 8
Перевод любого числа в десятичную
систему счисления:
Нужно
воспользоваться многочленом
А (s)=ansn+an-1sn-1+…+a-ms-m
Например:
4 3 2 1
010111=1•24+0•23+1•22+1•21+1•20=16+4+2+1=2310
2 1 0
2213=2•32+2•31+1•30=2•9+2•3+1=18+6+1=2510





























