- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методическая разработка по информатике и икт (10 класс) по теме: Системы счисления.
Содержание
- 2. Перевод чисел из двоичной СС в десятичнуюДля
- 3. примерПеревести из двоичной системы счисления в десятичную
- 4. Арифметические действия в двоичой системе счисленияВсе действия
- 5. ВычитаниеВычитание выполняется по следующим правилам:0-0=01-0=11-1=010-1=1
- 6. Выполнить в
- 7. Примеры Выполнить самостоятельно вычитание двоичных чисел:а)111-101
- 8. Восьмиричная система счисленияПредставление чисел в ВСС:
- 9. Перевод чисел из десятичной
- 10. Перевод чисел из ВСС в дес.ССПеревести 25738
- 11. Перевод из восьмиричной системы счисления
- 12. Перевести число 6573258 в двоичную систему счисленияДля
- 13. Перевод из двоичной системы
- 14. Шестнадцатиричная система счисленияФормула представления чисел в шестнадцитиричной
- 15. Перевод чисел из десятичной системы счисления в
- 16. Перевод числа из
- 17. ПримерПеревести 1АFB916 в десятичную систему счисления.1АFB916 = =1*164+10*163+15*162+11*161+9*160==1*65534+10*4096+15*256+11*16+9*1== 65534+40960+3840+176+9=11052110
- 18. Перевод чисел из ШСС в двоичную и
- 19. Таблица эквивалентов цифр
- 20. примерПеревести AF19316 в двоичную систему счисления.
- 21. ПримерПеревести из двоичной системы счисления в шестнадцатиричную
- 22. Скачать презентацию
- 23. Похожие презентации
Перевод чисел из двоичной СС в десятичнуюДля перевода чисел из двоичной системы счисления в десятичную выполняется накопление суммы произведений коэффициентов в разрядах двоичного числа на соответствующие степени основания системы счисления (g=2)



















Слайд 3
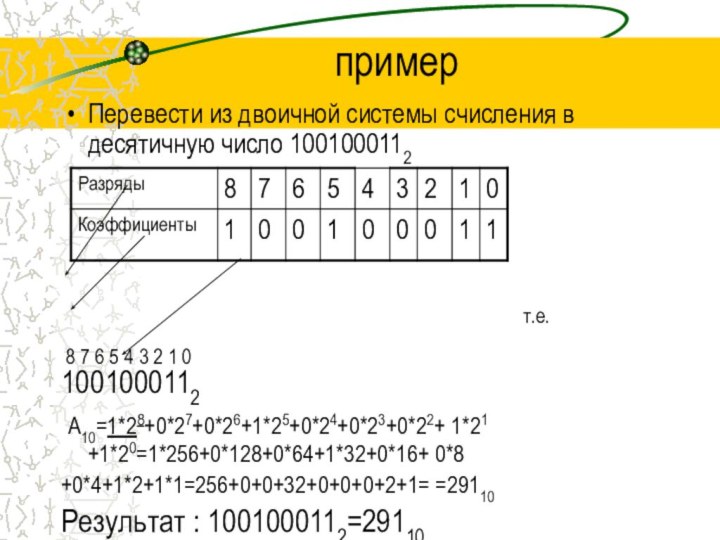
пример
Перевести из двоичной системы счисления в десятичную число
1001000112
т.е.8 7 6 5 4 3 2 1 0
1001000112
А10=1*28+0*27+0*26+1*25+0*24+0*23+0*22+ 1*21 +1*20=1*256+0*128+0*64+1*32+0*16+ 0*8
+0*4+1*2+1*1=256+0+0+32+0+0+0+2+1= =29110
Результат : 1001000112=29110
Слайд 4
Арифметические действия в двоичой системе счисления
Все действия В
ЭВМ сводятся к сложению.
Составим таблицу сложения в двоичной системе
счисления0+0=0
0+1=1
1+1 =10 (Почему ?)
Слайд 6 Выполнить в двоичной
системе счисления сложение и вычитание чисел: 1011011 и 1001111
а)
1011011 б)1011011+ 1001111 - 1001111
10101010 1100
Слайд 7
Примеры
Выполнить самостоятельно вычитание двоичных чисел:
а)111-101
в) 11011-1110
б) 10001-100
г) 11011-1010
Слайд 8
Восьмиричная система счисления
Представление чисел в ВСС:
А8=а0*80+а1*81+а2*82+…+аn*8n
Сколько цифр используется в этой системе счисления? Какие?
При переходе
цифры из разряда в разряд ее значение увеличивается или уменьшается в 8 раз.Слайд 9 Перевод чисел из десятичной системы
счисления в восьмиричную
Перевод чисел из десятичной системы счисления в
восьмиричную осуществляется методом последовательного деления.Перевести из десятичной системы счисления в восьмиричную число 25.
25 8 Результат: 2510=318
24 3 8
1 0 0
3
Слайд 10
Перевод чисел из ВСС в дес.СС
Перевести 25738
в десятичную систему счисления.
3 2 1 02573
А10=2*83+5*82+ 7*81+3*80 =1024+320+56+3=1403
Результат : 25738=140310
Слайд 11 Перевод из восьмиричной системы счисления в
двоичную и обратно
Для перевода пользуются таблицей эквивалентов цифр восьмиричной
и двоичной системы cчисления.
Слайд 12
Перевести число 6573258 в двоичную систему счисления
Для этого
заменим все цифры в восьмиричном числе их эквивалентами в
двоичной системе счисления:6 5 7 3 2 5
101 111 011 010 101
Результат : 6573258=1101011110110101012
Слайд 13 Перевод из двоичной системы счисления
в восмиричную
Для перевода чисел из двоичной системы счисления в
восьмиричную разбиваем число на группы из 3-х цифр, начиная с младшего разряда, и заменяем их эквивалентами в восьмиричной системе счисления.Пример: 110101011001112=?8
11 010 101 100 111
3 2 5 4 7
Результат: 110101011001112=325478
Слайд 14
Шестнадцатиричная система счисления
Формула представления чисел в шестнадцитиричной системе
счисления
А16=а0*160+а1*161+а2*162+…+аn+1*16n
Сколько цифр используется в этой системе счисления? Какие?
0,1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),
E(14), F(15).Слайд 15 Перевод чисел из десятичной системы счисления в шестнацатиричную
и обратно
Для перевода чисел из десятичной системы счисления в
шестнацатиричную используется метод последовательного деления.Пример. Перевести число 5610 в шестнацатиричную.
56 16
3 16 Результат: 5610= 3816
8 0 0
3
Слайд 16 Перевод числа из шестнацатиричной
системы счисления в десятичную
Чтобы перевести число из шестнадцатиричной системы
счисления в десятичную, нужно вычислить сумму произведений коэффициентов в разрядах на соответствующие степени основания системы счисления (16).
Слайд 17
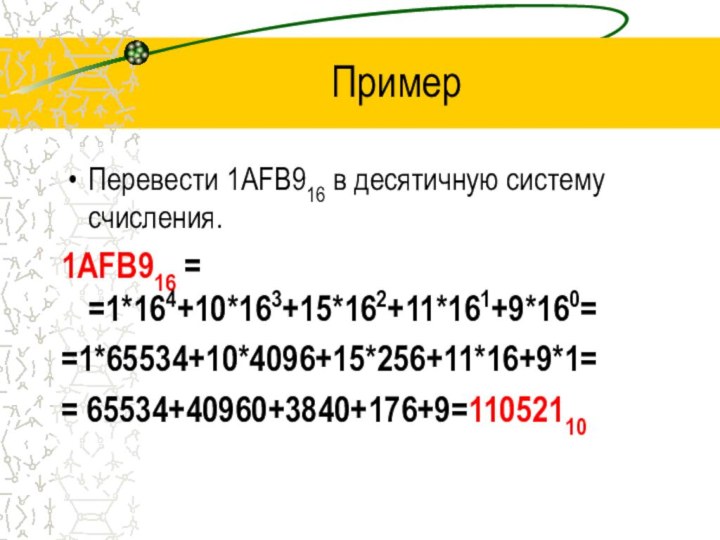
Пример
Перевести 1АFB916 в десятичную систему счисления.
1АFB916 = =1*164+10*163+15*162+11*161+9*160=
=1*65534+10*4096+15*256+11*16+9*1=
=
65534+40960+3840+176+9=11052110
Слайд 18
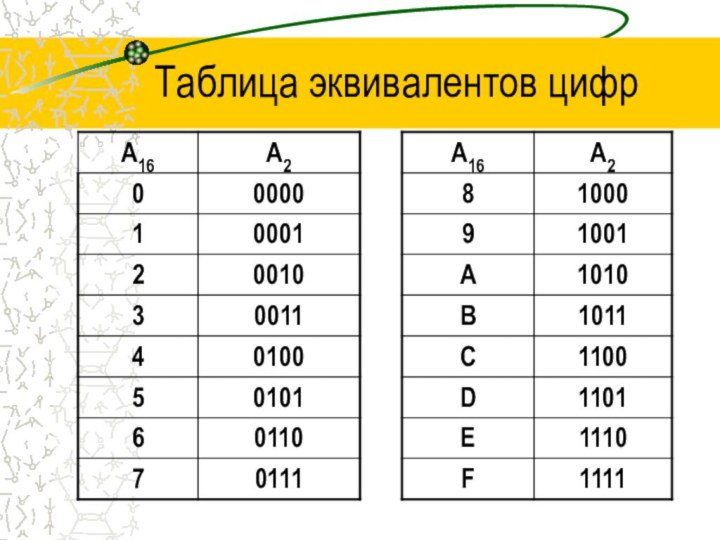
Перевод чисел из ШСС в двоичную и обратно
Чтобы
перевести число из шестнацатеричной системы счисления в двоичную и
для обратного перевода чисел, используют таблицу эквивалентов цифр в шестнацатеричной и двоичной системах счисления.
Слайд 20
пример
Перевести AF19316 в двоичную систему счисления.
A
F 1
9 31111 0001 1001 0011
Результат:
AF19316 =101011110001100100112
Слайд 21
Пример
Перевести из двоичной системы счисления в шестнадцатиричную число
11011001001110102
Начиная с младшего разряда, разобьем число на группы из
4-х цифр(квадры). Пользуясь таблицей заменим квадры из эквивалентами в шест.сист счисл.1001 0011 1010
D 9 3 A
Результат: 11011001001110102= D93A16





























