Слайд 2
Немного теории:
Алгоритм-это понятное и точное
предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных
данных к искомому результату.
Каждая команда алгоритма должна определять однозначное действие исполнителя.
Исполнение алгоритма должно завершиться за конечное число шагов.
http://files.school-collection.edu.ru/dlrstore/58e9a0c3-11df-4c94-a5eb-b0a7b359ea35/9_32.swf
Слайд 3
Задачи на формальное исполнение алгоритма включены
в ЕГЭ по информатике в часть А (заданиеА5) и
часть В (задание В1).
Уровень сложности обоих заданий- базовый, максимальный балл за верное решение-1.
Время выполнения задания А5-
1 мин.,задания В1-4 мин.
Слайд 4
Задача 1
Автомат получает на вход два трехзначных шестнадцатеричных
числа. В этих числах все цифры не превосходят цифру
8( если в числе есть цифра больше 8, автомат отказывается работать).По этим числам строится новое число по следующим правилам:
Вычисляются три числа-суммы старших, средних и младших разрядов полученных чисел.
Полученные три шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).
Пример: Исходные трехзначные числа 285 и 767. Поразрядные суммы:9,Е,С.Результат:ЕС9.
Определите, какое из следующих чисел может быть результатом работы автомата.
1)СА11 2)1198 3)9АС 4)F98
Слайд 5
Решение:
1) Шестнадцатеричное число СА11 состоит из шестнадцатеричных цифр
С,А,1,1,следовательно, может являться только результатом сложения четырехзначных чисел.
2) Шестнадцатеричное
число 1198 состоит из шестнадцатеричных цифр 1,1,9,8 ,аналогично, является только результатом сложения четырехзначных чисел.
3) Шестнадцатеричное число 9АС состоит из шестнадцатеричных цифр 9¹,А²и С³, которые расположены в порядке возрастания.
4) В числе F98 шестнадцатеричные цифры F³,9² и 8¹расположены в порядке убывания. Таким образом, это число может являться результатом работы автомата.
Слайд 6
Задача 2
Автомат получает на вход два четырехзначных числа.
По этим числам строится новое число по следующим правилам:
Вычисляются
четыре числа – сумма цифр, стоящих в разряде тысяч, сумма цифр, стоящих в разряде сотен, сумма цифр, стоящих в разряде десятков этих чисел и сумма цифр младших разрядов.
Полученные четыре числа записываются друг за другом в порядке возрастания (без разделителей).
Пример: Исходные четырехзначные числа: 2788 и 4152. Поразрядные суммы: 6,8,13,10.
Результат: 681013
Определите, какое из следующих чисел может быть результатом работы автомата.
1) 10111619 2)9111518 3)23809 4)11151115
Слайд 7
Решение:
10111619 состоит из поразрядных сумм 10,11,16 и 19.
При этом число19 не может быть результатом сложения двух
однозначных чисел.
Число 23809 состоит из поразрядных сумм 2,3,8,0,9,т.е. является результатом сложения пятизначных чисел.
Число 11151115 состоит из поразрядных сумм
11,15,11,15 которые записаны не в порядке возрастания.
4) Число 9111518 состоит из поразрядных сумм 9,11,15 и 18,записанных в порядке возрастания, следовательно, оно может быть результатом работы автомата.
Слайд 8
Задача 3.
У исполнителя
Калькулятор имеется только две команды:
Прибавь 1.
Умножь на 2.
Выполняя первую из них Калькулятор прибавляет к числу на экране +1, а выполняя вторую удваивает его. Запишите порядок команд в программе получения из 3 числа 25, содержащей не более 5 команд, указывая лишь номера команд.
Слайд 9
Решение:
Число 25 не делится на 2,
поэтому вычтем из него 1.
Полученное число
24 целесообразно разделить на 2.Число 12
опять делим на 2, и ,окончательно, при делении на 2 числа 6
получаем заданное число 3.
Цепочку вычислений запишем в обратном порядке:
3·2=6 (команда 2 Калькулятора)
6·2=12 (команда 2 Калькулятора)
12 ·2=24 (команда 2 Калькулятора)
24+1=25 (команда 1 Калькулятора)
Ответ: 2221
Слайд 10
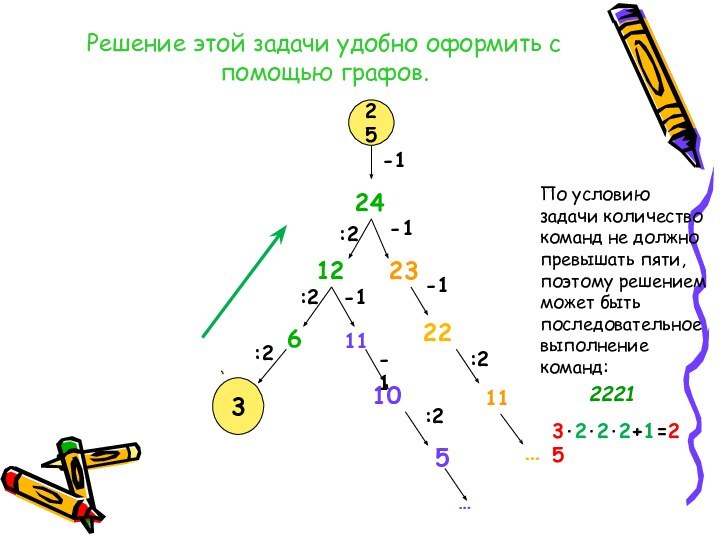
Решение этой задачи удобно оформить с помощью графов.
По условию задачи количество команд не должно превышать пяти, поэтому решением может быть последовательное выполнение команд:
2221
-1
24
-1
12
23
:2
-1
:2
3
-1
10
:2
5
…
25
6
:2
11
-1
22
:2
11
…
3⋅2⋅2⋅2+1=25
Слайд 11
Задачи для самостоятельного решения
Слайд 12
Задача 4
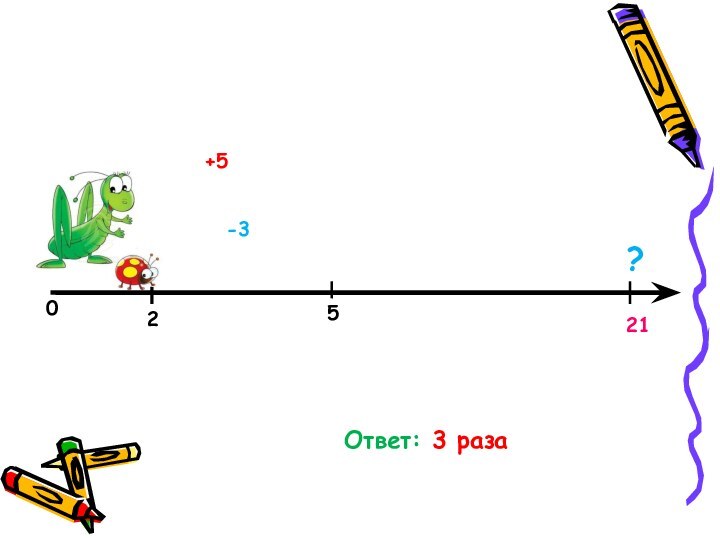
Исполнитель КУЗНЕЧИК живёт на числовой
оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд
Кузнечика:
Вперед 5 – Кузнечик прыгает вперёд на 5 единиц,
Назад 3 – Кузнечик прыгает назад на 3 единицы.
Какое наименьшее количество раз должна встретиться в программе команда «Назад 3», чтобы Кузнечик оказался в точке 21?
Слайд 14
Задача5
Вася забыл пароль к Windows XP,
но помнил алгоритм его получения из строки подсказки «B265C42GC4»:
если все последовательности символов «C4» заменить на «F16», а затем из получившейся строки удалить все трехзначные числа, то полученная последовательность и будет паролем. Определите пароль:
1) BFGF16
2) BF42GF16
3) BFGF4
4) BF16GF
Ответ:BFGF16