Презентация на тему к уроку Системы счисления

курса информатики историей развития и классификацией различных систем счисления,

с алгоритмом перевода из десятичной системы счисления в другие(двоичная, восьмеричная, шестнадцатеричная).

Используемые информационные продукты:
Microsoft Power Point - для создание и демонстрации презентации;
Microsoft Word - для набора текста;
Paint - для создания графических объектов;
Adobe Photoshop - для редактирования графических объектов;


Системные требования:
Презентацию можно выполнить на компьютере любого класса где содержаться Win98/ME/2000/XP
Программа Microsoft Power Point любой версии.
Особых ограничений НЕТ.

Содержание проекта:
Основные темы:
История системы счисления
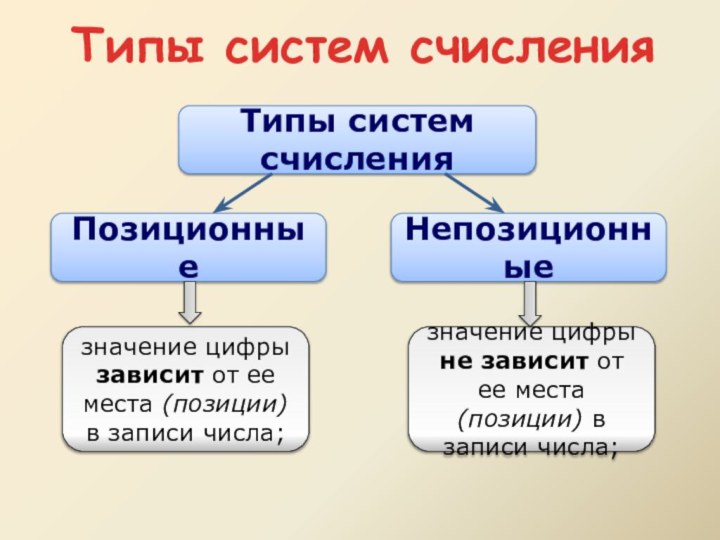
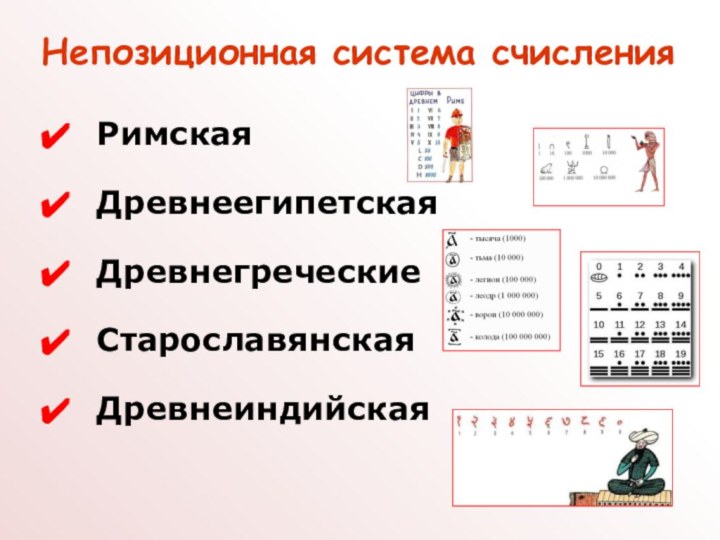
Непозиционные системы счисления
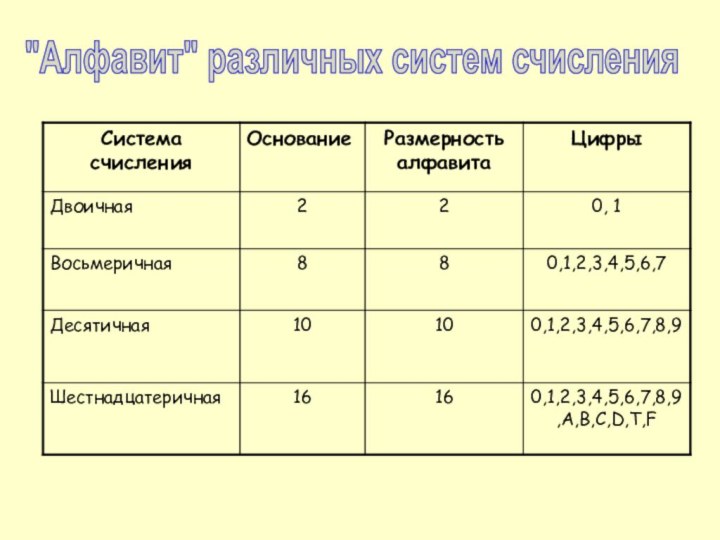
Позиционные системы счисления
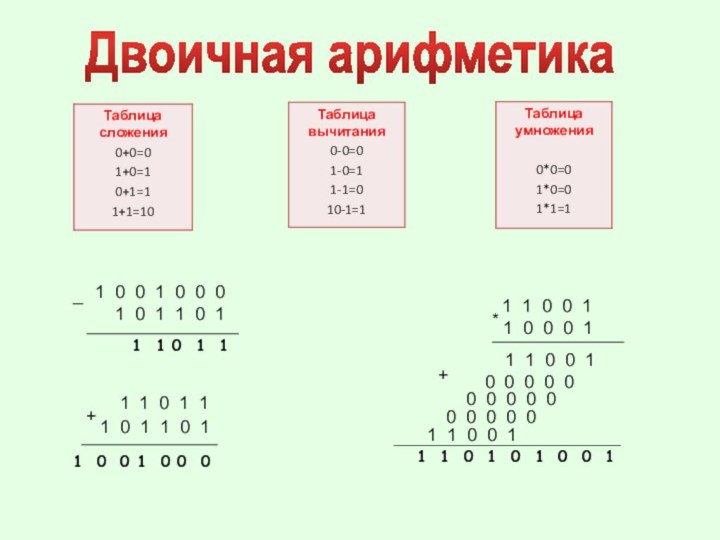
Двоичная арифметика
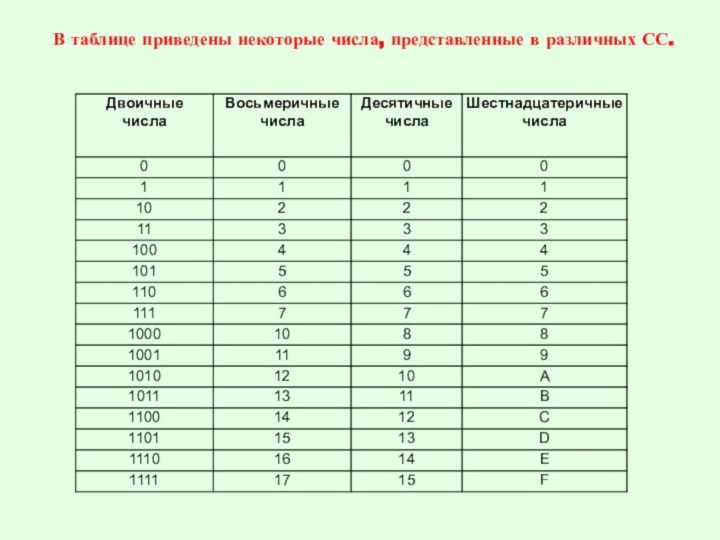
Алгоритм перевода чисел из одной системы счисления в другую

отличается цифра от числа?
Для записи информации о количестве объектов

используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления.
Знаки системы счисления, с помощью которых записывают числа – это цифры.

Цифр ограниченное количество, а чисел бесконечно много!

потребность в записи чисел.
Количество предметов изображалось нанесением равного

количества черточек, зарубок или засечек на какой-либо твердой поверхности.

Унарная система счисления

Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.

Раскопки относятся к периоду палеолита (10–11 тысяч лет до н.э.)

до н.э.
Каждый символ повторяется определенное число раз, и, чтобы

прочитать число, нужно просуммировать значения всех символов, входящих в его запись.

Греции была распространена так называемая Аттическая система счисления, название

происходит от области Греции– Аттики со столицей Афины.

нечасто, но достаточно долго.
По организации повторяет греческую нумерацию.

Использовалась она с VIII по XIII в.

Алфавитная система была принята и в Древней Руси. Получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел.
Была создана для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке.

веков, номера глав в книгах, циферблат часов
Для записи чисел

используются буквы латинского алфавита

от большей
IX (10-1=9)

если меньшие цифры стоят справа от большей
XII

(10+1+1=12)

не ставят больше трех одинаковых цифр подряд

Примеры:

–

+

D X L I I

= 542

X X X I I

= 32

98 = XCVIII

99 = XCIX

100 = C

101 = CI

102 = CII

97 = XCVII

70 + 9 = MCCLXXIX
M
CC
LXX
IX
1279
MCDLXIV
Переведите числа

в римскую СС и обратно.

CMXVII =
MMCXXIX=
MCMLXIII =

405 =
1984 =
2983 =

Самостоятельно:

записи больших чисел.
Невозможно представлять дробные и отрицательные числа.
Сложно выполнять

арифметические операции, так как не существует алгоритмов их выполнения.

ее позицией в записи числа.
Десятичная
Вавилонская (шестидесятиричная)
Племена индейцев Майя

(двадцатеричная)
Двенадцатеричная (древняя Шумера)
В компьютерной технике (двоичная, восьмеричная, шестнадцатеричная)

основанная на позиционном принципе.
Числа менее 60 обозначались с помощью

двух знаков:
прямой клин служил для обозначения единиц, лежачий клин – для обозначения десятков.

- единицы


- десятки

Вавилонская система счисления

- ноль

Древний Вавилон
(II тысячелетие до нашей эры)

ацтеков и майя, населявших американский континент и создавших там

высокую культуру, почти полностью уничтоженную испанскими завоевателями в XVI - XVII в., была принята двадцатеричная система счисления.

800 г.н.э. – заимствована арабами в 1200 г.н.э. - начали

применять в Европе,
В Европе они стали известны благодаря трудам арабских математиков, и потому за ними утвердилось название «арабские», хотя сами арабы вплоть до настоящего времени пользуются совсем другими символами.
Арабские цифры:
В России арабская нумерация стала использоваться при Петре I (до конца XVII века сохранилась славянская нумерация)

Самая распространенная на сегодняшний день нумерация, которой мы пользуемся в настоящее время.

0 1 2 3 4 5 6 7 8 9

-восьмеричная
-шестнадцатеричная
позиционные системы счисления.

цифр:
0, 1, 2, 3, 4, 5, 6, 7,

8, 9

Именно поэтому наша современная система счисления называется десятичной.
Известный русский математик Н.Н.Лузин так выразился по этому поводу:

«Преимущества десятичной системы счисления не
математические, а зоологические. Если бы у нас было на
руках не десять пальцев, а восемь, то человечество бы
пользовалось восьмеричной системой счисления.»

Десятичная система счисления

двоичной арифметики связано с именем Г. В. Лейбница, опубликовавшего

в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами. Ее недостаток – «длинная» запись чисел.

В настоящий момент – наиболее употребительная в информатике, вычислительной технике и смежных отраслях система счисления. Использует две цифры: 0 и 1
Пример:
Свернутая форма записи числа: 1012
2 1 0
Развернутая форма: 101 =1*22 +0*21+1*20
Все числа в компьютере представляются
с помощью нулей и единиц, т. е.
в двоичной системе счисления.

Двоичная система счисления

данной системы счисления,
n-число разрядов целой части числа,
m-число

разрядов дробной части числа.
Пример:

Развернутая форма записи числа

единицы

десятки

сотни

тысячи

СС.

число в развернутой форме. При этом основание с/с должно

быть представлено в десятичной системе счисления.
2. Найдите сумму ряда. Полученное число является значением числа в десятичной системе счисления.
 Примеры:
Переведем число 110012 в десятичную систему счисления.
1. Запишем число в развернутой форме:
11012 = 124+123 + 022 + 021 + 120.
2. Найдем сумму ряда: 24+23+0+0+20 = 16+8+4+1 = 2910.
 Переведем число 16,48.
1. Запишем число в развернутой форме: 181+680+48-1
2. Найдем сумму: 8+6+0,5 = 14,510.

перевода целых чисел из десятичной системы счисления в любую

другую:

1. Последовательно выполнить деление данного числа и получаемых целых частных на основание новой с/с, пока не получится частное, меньшее делителя.
2. Полученные остатки являются цифрами числа в новой с/с.
3. Составить число в новой системе счисления, записывая его начиная с последнего остатка.

8
х 8
4
5000
Двоичная
Восьмеричная
Шестнадцатеричная

1 0 1
1 0 0 1 0 0

0

+

1 0 0 1 0 0 0

1 0 1 1 0 1

1 1 0 1 1

_

1 1 0 0 1

1 0 0 0 1

*

1 1 0 0 1

0 0 0 0 0

0 0 0 0 0

0 0 0 0 0

1 1 0 0 1

+

1 1 0 1 0 1 0 0 1

В портфеле по 100 книг носила.
Все это правда, а

не бред.
Когда пыля десятком ног.
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий,
Она ловила каждый звук
Своими десятью ушами,
И 10 загорелых рук
Портфель и поводок держали.
И 10 темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным,
Когда поймете наш рассказ.

Задача

В портфеле по 4 книг носила.
Все это правда, а

не бред.
Когда пыля десятком ног.
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий,
Она ловила каждый звук
Своими десятью ушами,
И 2 загорелых рук
Портфель и поводок держали.
И 2 темно-синих глаз
Оглядывали мир привычно.
Но станет все совсем обычным,
Когда поймете наш рассказ.