Презентация на тему Основы формальная и математической логики. 11 класс

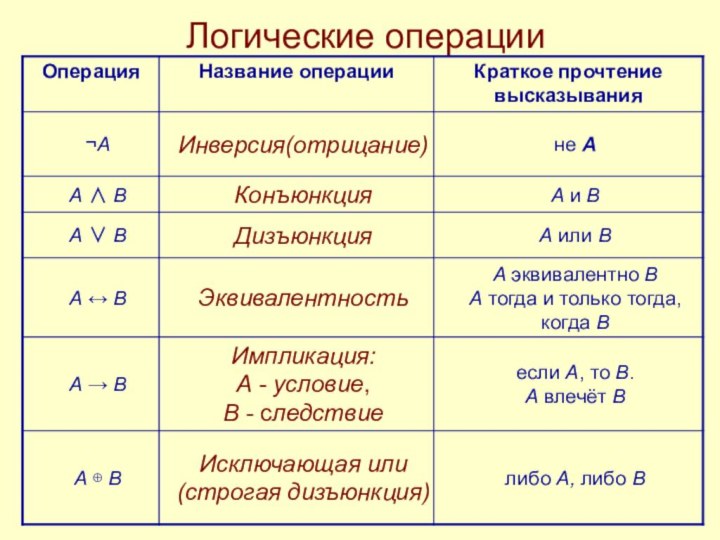
понятие, рассуждение, закон

Формальная логика – наука о законах

и формах мышления

Основные формы мышления:
Понятие – это форма мышления, которая выделяет признаки предмета или класса предметов, отличающие его от других
Суждение – это мысль, в которой что-то утверждается или отрицается о предметах
Умозаключение – прием мышления, позволяющий на основе одного или нескольких суждений-посылок получить новое суждение (знание или вывод)

Математическая логика – наука о применении математических методов в решении логических задач

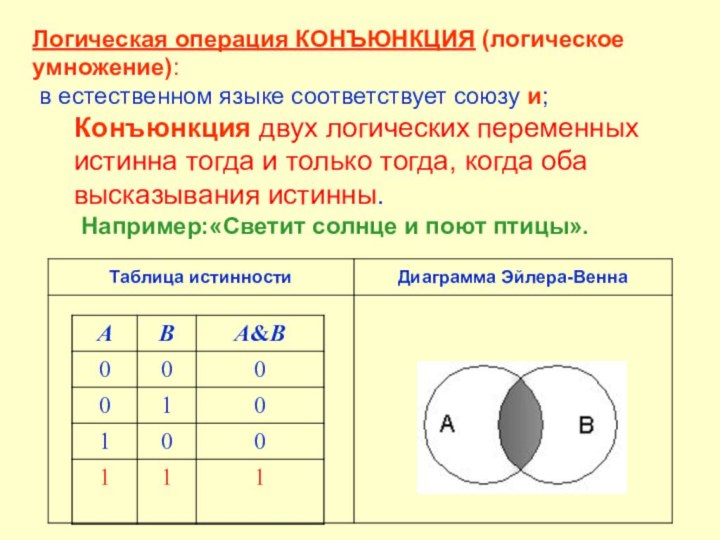
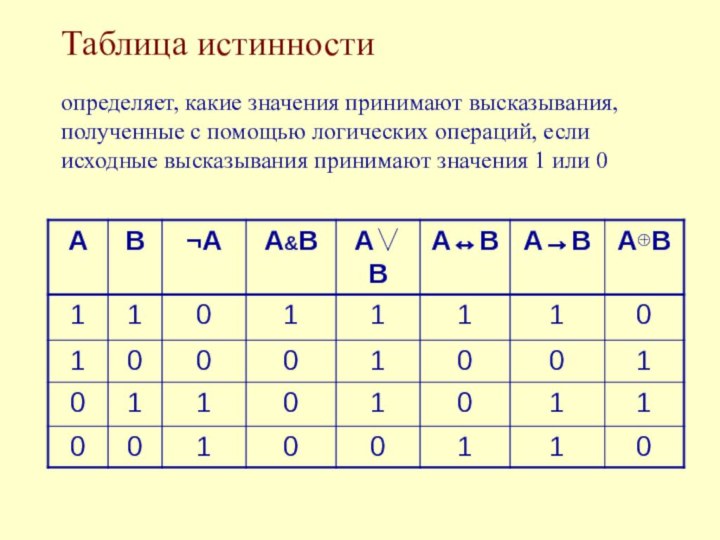
Суждения - суть высказывания или логические выражения

Алгебра высказываний или алгебра логики - раздел математической логики для обработки логических выражений

Аристотель

можно сказать, истинно оно или ложно.
Примеры высказываний:
«Листва

на деревьях опадает осенью»;
«Зимой в Московской области нет зеленых деревьев».
Сложное высказывание получается из простых или сложных высказываний с использованием союзов-связок И, ИЛИ и частицы НЕ
Например:«Ученик прогулял урок и получил двойку».

Формальная логика

Вы были в театре?
Завтра я не пойду на каток.
Мойте руки перед едой.
Если будет дождь, то мы поедем за грибами
Луна — спутник Земли.
Если я поеду туда, то смогу ли вернуться?
IF X>1 THEN Y=0
Принеси мне книгу.
Некоторые люди имеют голубые глаза
Существуют такие люди, которые не любят животных.

Задание№2
Укажите среди нижеприведенных высказываний, сложные они или простые:
Если две прямые параллельны, то они пересекаются
Идет дождь.
Все мышки серые, кошки тоже бывают серые.
На следующем уроке будет либо контрольная, либо свободный урок.
Треугольники с равными сторонами не равнобедренны
7 +х>х + с + 0,1а
Число 3 больше числа 2.

может принимать лишь два значения 1(истина) и 0 (ложь)

Логическая функция – сложное логическое выражение, составленное из логических переменных

Алгебра логики (Булева алгебра )

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель - основоположник логики}
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.

Дж. Буль

и частице не; обозначение —, ¬;
Инверсия логической переменной

истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Пример инверсии: «Завтра я не приду к тебе».

языке соответствует союзу и;
Конъюнкция двух логических переменных истинна

тогда и только тогда, когда оба высказывания истинны.
Например:«Светит солнце и поют птицы».

или; обозначение +; V; 
Дизъюнкция двух логических переменных ложна

тогда и только тогда, когда оба высказывания ложны.
Например: «В отпуске мы будем посещать театры или выставки».
Дизъюнкцию называют также двоичным сложением с одной оговоркой: по правилу двоичного сложения 1 + 1 = 10, а в нашем примере 1 + 1 = 1.

языке соответствует обороту если ..., то ...;
обозначение →;⊃
Импликация

двух логических переменных ложна только тогда, когда предпосылка истинна, а заключение ложно, и истинна – во всех остальных случаях.
Пример импликации: «Если завтра будет тепло, то мы пойдем гулять».

оборотам речи тогда и только тогда; в том и

только в том случае;
обозначения ≡;↔,~
Эквивалентность двух логических переменных истинна только тогда, когда обе переменные одновременно истинны или одновременно ложны.
Пример эквивалентности: «Я заведу себе щенка тогда и только тогда, когда хорошо изучу, как надо с ним обращаться.»

соответствует оборотам речи либо… , либо.. обозначение ⊕, \./
Строгая

дизъюнкция логических переменных истинна тогда только тогда, когда истинна только одна из логических переменных.
Пример строгой дизъюнкции: «Саша либо дома, либо вышел погулять с собакой».

с помощью логических операций, если исходные высказывания принимают значения

1 или 0

она пишется раздельно со словом;
б) рыбу ловят сачком или

ловят крючком, или мухой приманивают, иль червячком;
в) буква «а» – первая буква в слове «аист» или «сова»;
г) данное число четно или число, больше его на единицу, четно.
Используя логические операции, запишите высказывания, которые являются истинными:
а) неверно, что и ;
б) является ;
в) X ,Y,Z равны между собой;

Упражнения