- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы счисления (8 класс)
Содержание
- 2. Определения Система счисления – это способ записи
- 3. Чем отличается принцип записи многозначных чисел римскими и арабскими цифрами?
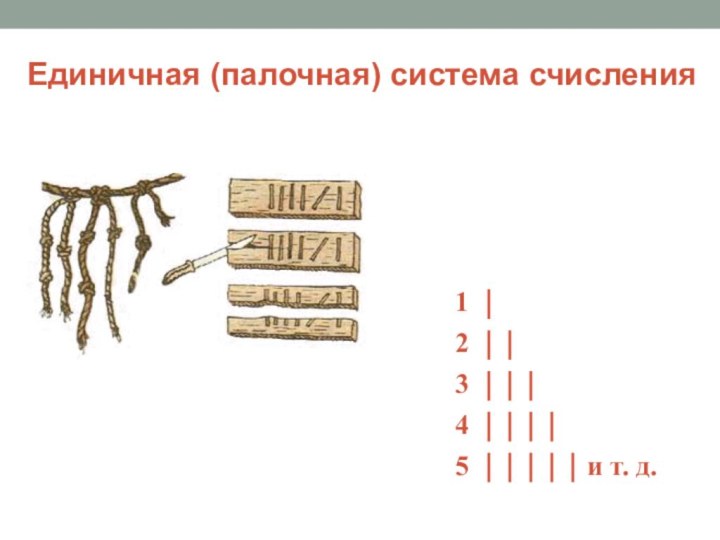
- 5. Единичная (палочная) система счисления
- 6. Древнеегипетская десятичная непозиционная система110100100010 000100 0001 000 00010 000 000Несколько единицНесколько десятков
- 7. Числа в египетской системе счисления записывались как
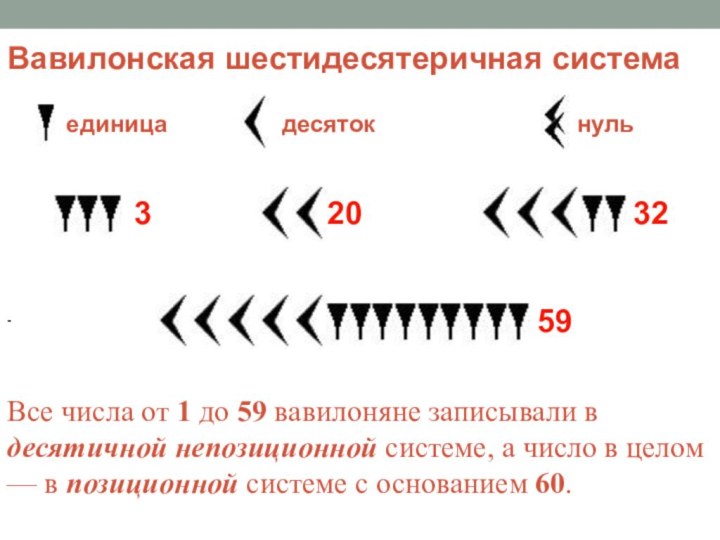
- 8. Вавилонская шестидесятеричная система- Все числа от 1
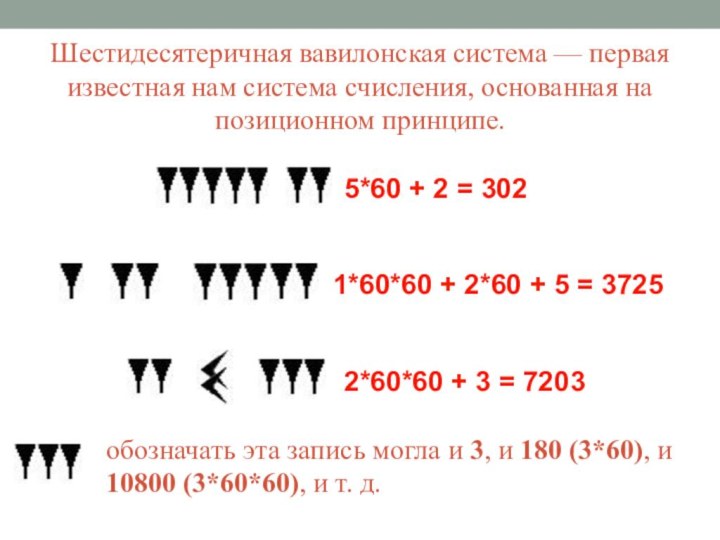
- 9. Шестидесятеричная вавилонская система — первая известная нам
- 10. Римская система записи чисел2006CCXXXVII = 100+100+10+10+10+5+1+1 =
- 11. Славянская глаголическая нумерация
- 12. Славянская кириллическая нумерация- 1000- 10 000
- 13. Китайская нумерация
- 14. Индийская мультипликативная системаПозиционная десятичная система счисления возникла
- 15. Книга Аль Хорезми была переведена в Западной
- 16. Эволюция цифр «губар»
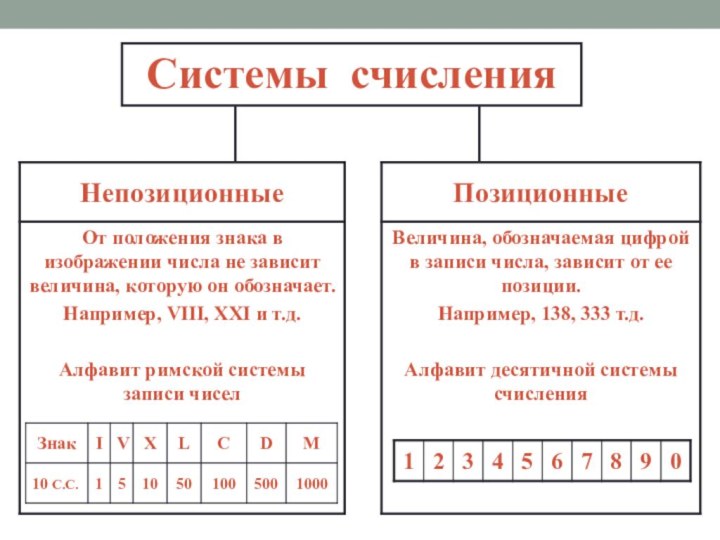
- 17. Непозиционные системы счисленияНепозиционной называют систему счисления, в
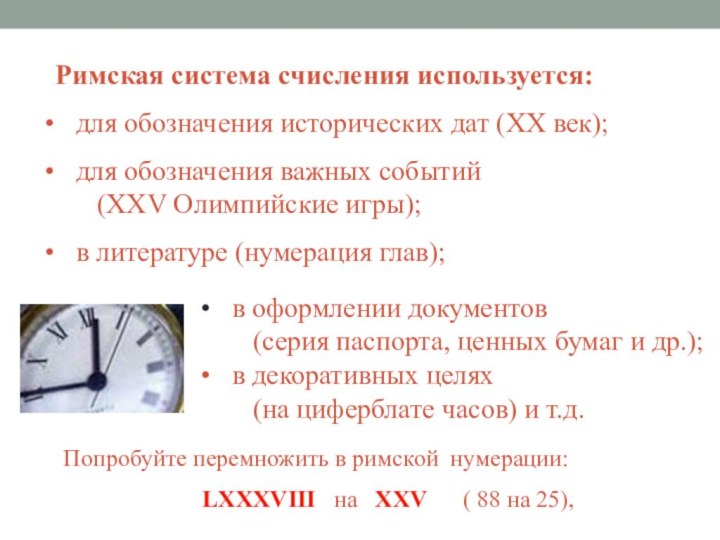
- 18. Римская система счисления используется: для обозначения
- 19. Недостатки непозиционных систем счисления: существует постоянная потребность
- 20. Позиционной называют систему счисления, в которой числовое
- 21. Позиционная десятичная система счисления123 = 1*102 +
- 22. Базис позиционной системы счисления — это последовательность
- 23. Число единиц какого-либо разряда, объединяемых в единицу
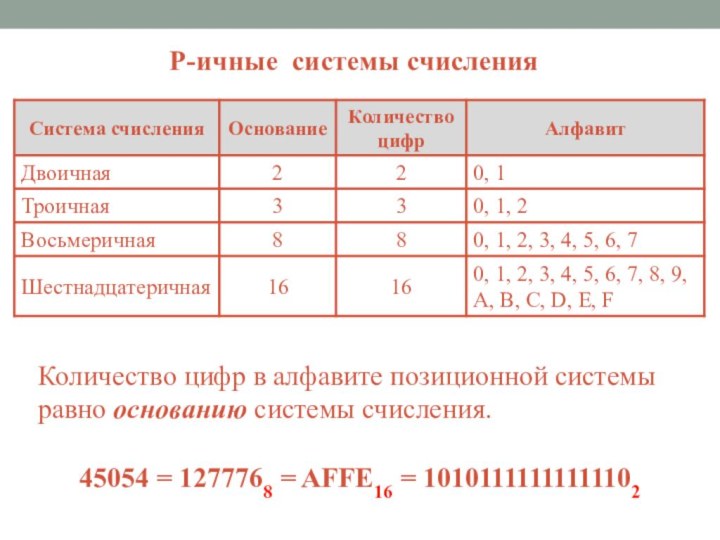
- 24. Количество цифр в алфавите позиционной системы равно
- 25. Представление чисел в Р-ичных системах счисленияРазвернутая форма
- 26. Десятичное число 61 можно записать:11110122021333143D1610611111012 = 1*25
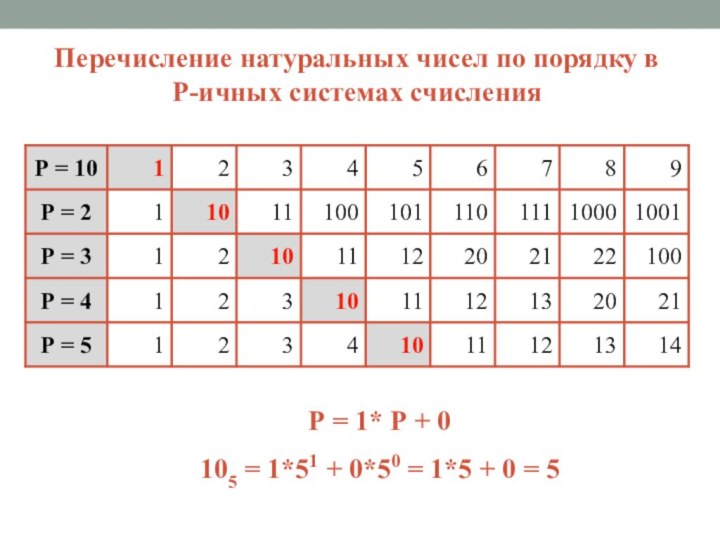
- 27. Перечисление натуральных чисел по порядку вР-ичных системах
- 28. Скачать презентацию
- 29. Похожие презентации





















Слайд 6
Древнеегипетская десятичная непозиционная система
1
10
100
1000
10 000
100 000
1 000 000
10
000 000
Несколько единиц
Несколько десятков
Слайд 7 Числа в египетской системе счисления записывались как комбинации
этих «цифр», в которых каждая «цифра» повторялась не более
девяти раз.Записывались цифры числа начиная с больших значений и заканчивая меньшими.
Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
Слайд 8
Вавилонская шестидесятеричная система
-
Все числа от 1 до
59 вавилоняне записывали в десятичной непозиционной системе, а число
в целом — в позиционной системе с основанием 60.Слайд 9 Шестидесятеричная вавилонская система — первая известная нам система
счисления, основанная на позиционном принципе.
обозначать эта запись могла и
3, и 180 (3*60), и 10800 (3*60*60), и т. д.
Слайд 10
Римская система записи чисел
2006
CCXXXVII = 100+100+10+10+10+5+1+1 = 237
XXXIX
= 10+10+10+10-1 = 39
CDXLIV = (D - С) +
(L - X) + (V - I) = 400 + 40 + 4 = 444 MDCCCXLIV = М + D + C + C + C + (L-X) + (V - I) = = 1000 + 500 + 100 + 100 + 100 + 40 + 4 = 1844
Слайд 14
Индийская мультипликативная система
Позиционная десятичная система счисления возникла приблизительно
в V веке н.э. в Индии.
Для записи числа
используется:определенное количество цифр;
цифра «0» для обозначения отсутствующего разряда;
разное значение цифры в зависимости от позиции в записи числа;
цифры изображаются символами алфавита "Деванагари".
Слайд 15 Книга Аль Хорезми была переведена в Западной Европе
на латинский язык в XII веке, и десятичная система
получила распространение во всей Европе под названием арабской.9999 → 9 * 1000 + 9 * 100 + 9 * 10 + 9
Чтобы "собрать" число используется умножение (multiplication англ.), поэтому систему и назвали "мультипликативной".
Решающую роль в распространении индийской нумерации в арабских странах сыграло руководство, составленное в начале IX века Мухаммедом Аль Хорезми, в котором он описал способы выполнения арифметических действий
Слайд 17
Непозиционные системы счисления
Непозиционной называют систему счисления, в которой
знаку, представляющему собой цифру, всегда соответствует определенное значение вне зависимости
от его местоположения в записи числа.Значение числа зависит от правил, предписывающих способ определения его значения.
Какой это год? MMVI
Слайд 18
Римская система счисления используется:
для обозначения исторических
дат (XX век);
для обозначения важных событий
(XXV Олимпийские игры);в литературе (нумерация глав);
Попробуйте перемножить в римской нумерации:
LXXXVIII на XXV ( 88 на 25),
в оформлении документов
(серия паспорта, ценных бумаг и др.);
в декоративных целях
(на циферблате часов) и т.д.
Слайд 19
Недостатки непозиционных систем счисления:
существует постоянная потребность введения
новых знаков для записи больших чисел;
отсутствуют формальные правила
записи чисел;отсутствуют алгоритмы выполнения арифметических действий с многозначными числами;
невозможно представлять дробные и отрицательные числа.
Слайд 20 Позиционной называют систему счисления, в которой числовое значение каждой
цифры (ее вес) зависит от номера ее позиции (разряда) в
последовательности цифр, представляющей число.Используется определенное количество цифр, которые изображаются определенными символами.
Совокупность различных цифр, используемых в позиционной системе счисления для записи чисел, называется алфавитом системы счисления.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Позиционные системы счисления
Слайд 21
Позиционная десятичная система счисления
123 = 1*102 + 2*101
+ 3*100 = 100 + 20 + 3
1023 =
1*103 + 0*102 + 2*101 + 3*100 = 1000 + 20 + 30,123 = 0,1 + 0,02 + 0,003 = 1*10-1 + 2*10-2 + 3*10-3
Число 10 называют основанием системы счисления,
а степени десятки - весами разрядов.
Слайд 22 Базис позиционной системы счисления — это последовательность чисел,
каждое из которых задает значение цифры «по месту» или
«вес» каждого разряда.Базисы традиционных систем счисления:
Десятичная система: 1, 10, 102, 103, 104, ..., 10n, ...
Двоичная система: 1, 2, 22, 23, 24, ..., 2n, ...
Восьмеричная система: 1, 8, 82, 83, 84, ..., 8n, ...
…, P-2, P-1, 1, P, P2, P3, …, Pn, …
Знаменатель P геометрической прогрессии, члены которой образуют базис позиционной системы счисления, называется основанием системы.
Слайд 23 Число единиц какого-либо разряда, объединяемых в единицу более
старшего разряда, называют основанием позиционной системы счисления.
Если количество таких
цифр равно P, то система счисления называется P-ичной.Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления .
Дополнительные определения
Слайд 24 Количество цифр в алфавите позиционной системы равно основанию
системы счисления.
45054 = 1277768 = AFFE16 = 10101111111111102
Р-ичные системы
счисления
Слайд 25
Представление чисел в Р-ичных системах счисления
Развернутая форма записи
числа
X=an*Pn + an-l*Pn-1 + ... + al*P + a0
+ b-1*P-1 + b-2*P-2 + ... + b-k*P-k + ...Свернутая форма записи числа
an an-1 … a1 a0 , b-1 b-2 … b-k …
Любое вещественное число можно записать в любой
Р-ичной системе счисления в виде суммы положительных и отрицательных степеней основания системы с помощью ограниченного набора цифр и при том единственным образом.
Слайд 26
Десятичное число 61 можно записать:
1111012
20213
3314
3D16
1061
1111012 = 1*25 +
1*24 + 1*23 + 1*22 + 0*21 + 1*20
== 32 + 16 + 8 + 4 + 1 = 61
20213 = 2*33 + 0*32 + 2*31 + 1*30 = 54 + 6 + 1 = 61
3314 = 3*42 + 3*41 + 1*40 = 48 + 12 + 1 = 61
3D16 = 3*161 + 13*160 = 48 + 13 = 61
1061 = 1*611 + 0*610 = 61