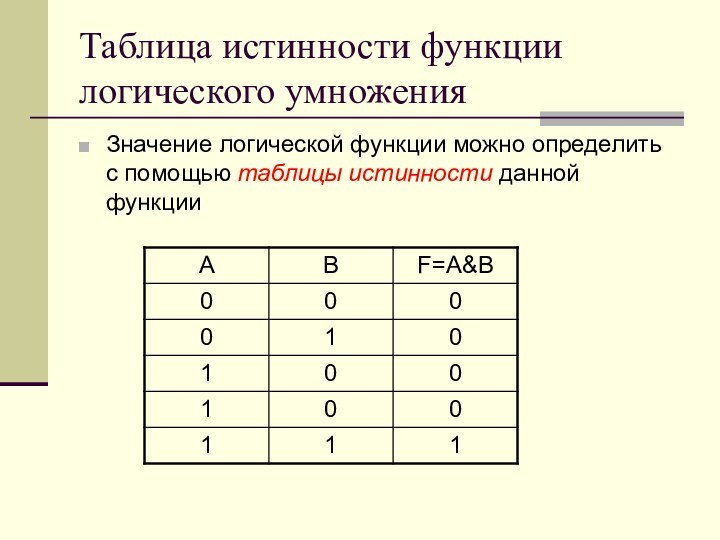
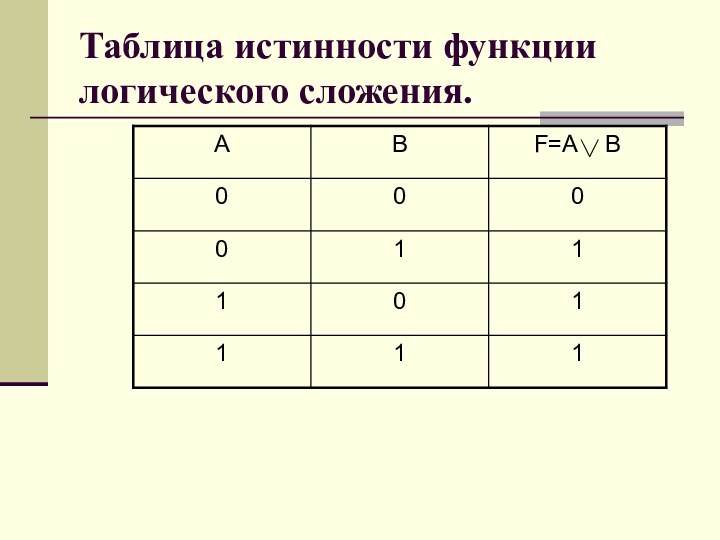
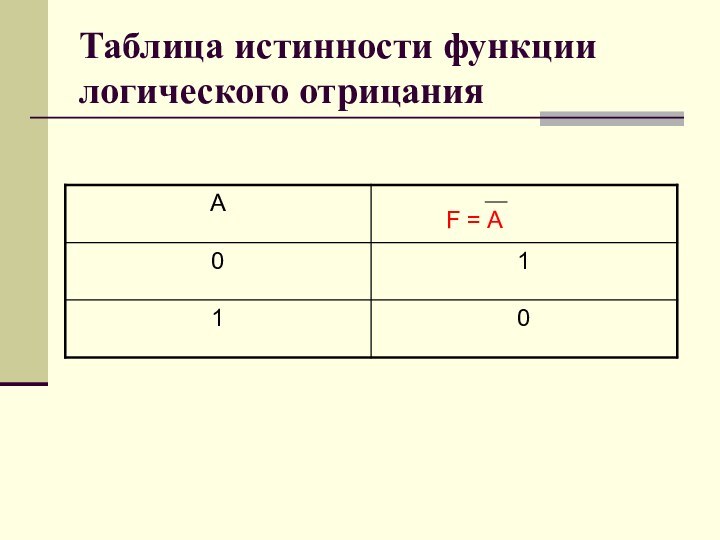
чтобы можно было определять истинность или ложность составных высказываний,
не вникая в их содержание.В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.