111
CEND
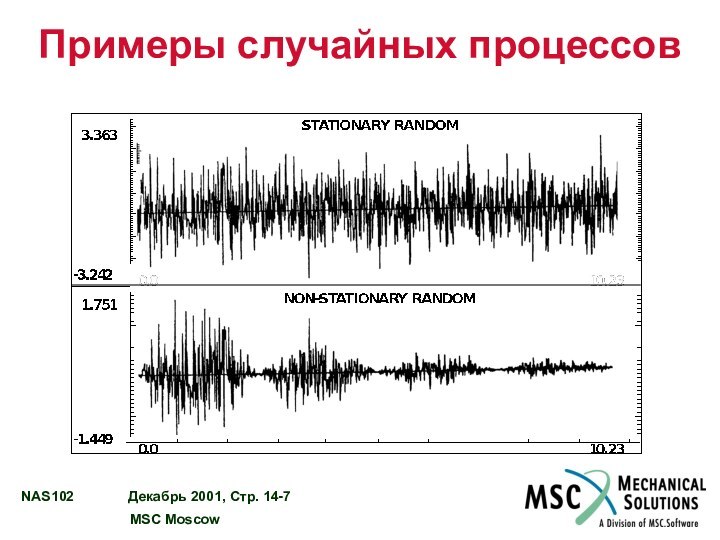
TITLE= RANDOM ANALYSIS - BASE EXCITATION
SUBTITLE= USING THE
MODAL METHOD WITH LANCZOS
ECHO= UNSORTED
SPC= 101
SET 111= 33, 55, 9999
ACCELERATION(SORT2, PHASE)= 111
METHOD= 100
FREQUENCY= 100
SDAMPING= 100
RANDOM= 100
DLOAD= 100
$
OUTPUT(XYPLOT)
XTGRID= YES
YTGRID= YES
XBGRID= YES
YBGRID= YES
YTLOG= YES
XTITLE= FREQUENCY
YTTITLE= ACCEL RESPONSE BASE, MAGNITUDE
YBTITLE= ACCEL RESPONSE AT BASE, PHASE
XYPLOT ACCEL RESPONSE / 9999 (T3RM, T3IP)
YTTITLE= ACCEL RESPONSE AT TIP CENTER, MAGNITUDE
YBTITLE= ACCEL RESPONSE AT TIP CENTER, PHASE
XYPLOT ACCEL RESPONSE / 33 (T3RM, T3IP)
YTTITLE= ACCEL RESPONSE AT OPPOSITE CORNER, MAGNITUDE
YBTITLE= ACCEL RESPONSE AT OPPOSETE CORNER, PHASE
XYPLOT ACCEL RESPONSE / 55 (T3RM, T3IP)
$
$ PLOT OUTPUT IS ONLY MEANS OF VIEWING PSD DATA
$
XGRID= YES
YGRID= YES
XLOG= YES
YLOG= YES
YTITLE= ACCEL P S D AT LOADED CORNER
XYPLOT ACCEL PSDF / 9999(T3)
YTITLE= ACCEL P S D AT TIP CENTER
XYPLOT ACCEL PSDF / 33(T3)
YTITLE= ACCEL P S D AT OPPOSITE CORNER
XYPLOT ACCEL PSDF / 55(T3)
$
BEGIN BULK
param,resvec,yes
PARAM,COUPMASS,1
PARAM,WTMASS,0.00259
$
INCLUDE 'plate.bdf'
$
GRID, 9999, , 0., 1., 0.
$
RBE2, 101, 9999, 12345, 1, 12, 23, 34, 45
$
SPC1, 101, 12456, 9999
$
$ EIGENVALUE EXTRACTION PARAMETERS
$
EIGRL, 100 , , 2000.
$
$ SPECIFY MODAL DAMPING
$
TABDMP1, 100, CRIT,
+, 0., .03, 10., .03, ENDT
$
$ POINT LOADING AT TIP CENTER
$
RLOAD2, 100, 600, , , 310,,A
spcd,600,9999,3,1.0
spc1,101,3,9999
$
TABLED1, 310,
+, 10., 1., 1000., 1., ENDT
$
$ SPECIFY FREQUENCY STEPS
$
FREQ,100,30.
FREQ1,100,20.,20.,50
FREQ4,100,20.,1000.,.03,5
$
$ SPECIFY SPECTRAL DENSITY
$
RANDPS, 100, 1, 1, 1., 0., 111
$
TABRND1, 111,LOG,LOG
+, 20., 0.1, 30., 1., 100., 1., 500., .1,
+, 1000., .1, ENDT
$
ENDDATA