Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Алгоритми на графах 1

Содержание

2. План лекціїЗагальні поняття/теоріяСім мостів КеніґсберґаСпособи представлення графів в задачахПошук в глибинуПошук в ширинуТопологічне сортуванняЗадача
3. Загальні поняттяГраф - це абстрактне представлення множини
4. Загальні поняттяВершини графа які з’єднані одним ребром
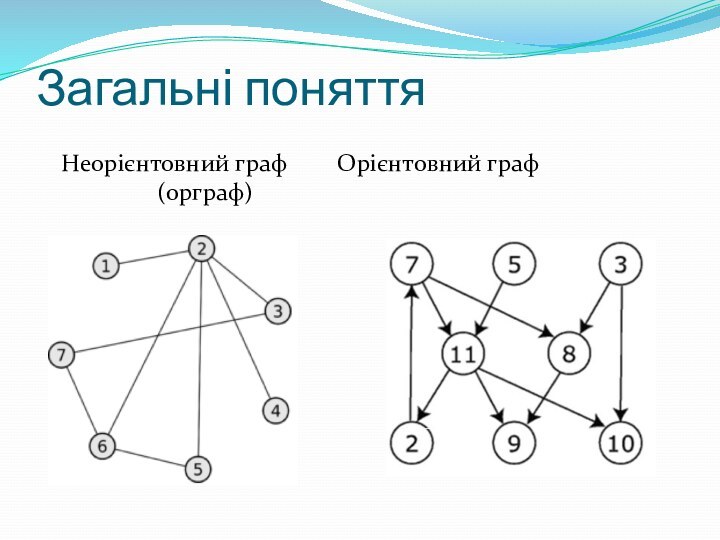
5. Загальні поняття Неорієнтовний граф Орієнтовний граф (орграф)
6. Загальні поняттяГраф називається зв’язним, якщо між будь-якою
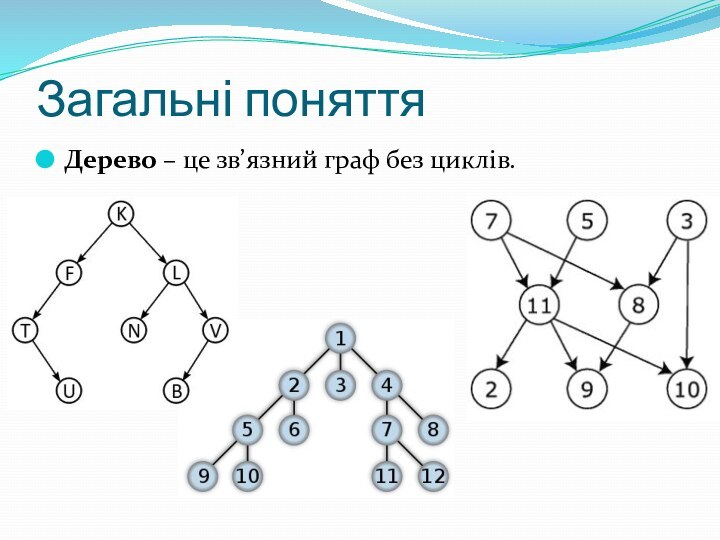
7. Загальні поняттяДерево – це зв’язний граф без циклів.
8. Загальні поняттяЗважений граф – граф який має
9. Сім мостів КеніґсберґаНеобхідно було знайти такий маршрут
10. Леонард Ейлер у 1735 р. довів що
11. Варіація задачіПівнічний берег річки зайнятий замком Синього
12. Синій Принц проаналізував міські мости з позиції
13. Способи представлення графівІснує два способи представлення графа:
14. Матриця суміжностіЦей спосіб є зручним для представлення
15. Матриця суміжностіДаний спосіб підходить для орієнтованих і
16. Список суміжностіПідходить для розріджених графів, тобто графів
17. Список суміжностіПам'ять необхідна для списку суміжності дорівнює
18. Пошук в глибинуDepth-first search, DFS - один з
19. Алгоритм пошуку в глибинуПроходимо по всіх вершинах,
20. Алгоритм пошуку в глибину з часовими міткамиДля
21. Використовується для вирішення задач:Пошук будь-якого шляху в
22. Пошук в ширинуBreadth-first search, BFS - один з
23. Пошук в ширину (демо)Порядок обходу вершинПроцес обходу
24. Алгоритм пошуку в ширинуПомістити вузол, з якого
25. Використовується для вирішення задач:Пошук найкоротшого шляху в
26. Топологічне сортуванняЦе таке впорядкування вершин направленого графа,
27. РеалізаціяТопологічне сортування реалізується за допомогою пошуку в
28. Задача 1Є одяг який треба одягти, і
29. Задача легко розв’язується за допомогою потологічного сортування
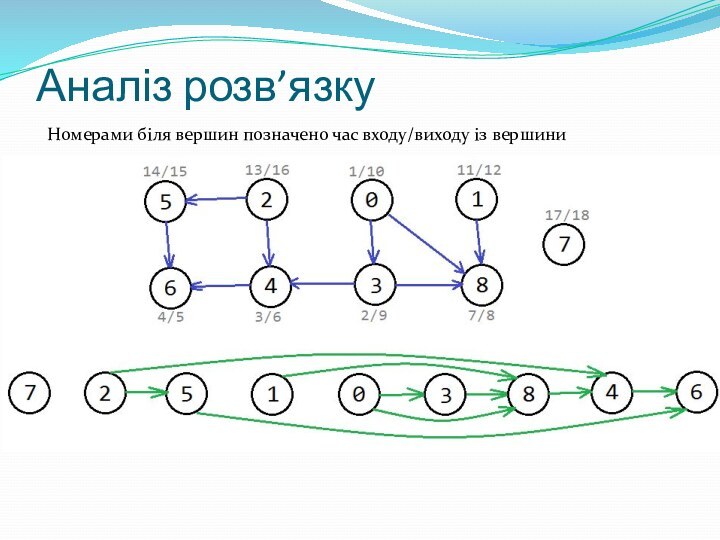
30. Аналіз розв’язкуНомерами біля вершин позначено час входу/виходу із вершини
31. Задача 2В останніх маркетингових дослідженнях було виявлено,
32. Аналіз розв’язкуЗадача може бути розв’язана пошуком в
33. Аналіз розв’язкуМаємо матрицю знайомств в якій m[i][j]=1,
34. Скачать презентацию
35. Похожие презентации

План лекціїЗагальні поняття/теоріяСім мостів КеніґсберґаСпособи представлення графів в задачахПошук в глибинуПошук в ширинуТопологічне сортуванняЗадача

Загальні поняттяГраф - це абстрактне представлення множини об'єктів і зв'язків між ними.Об’єкти

Загальні поняттяВершини графа які з’єднані одним ребром називають суміжними.У даному випадку вершини

Загальні поняття Неорієнтовний граф Орієнтовний граф (орграф)

Загальні поняттяГраф називається зв’язним, якщо між будь-якою парою вершин цього графа існує

Загальні поняттяДерево – це зв’язний граф без циклів.

Загальні поняттяЗважений граф – граф який має певну вагу ребер. Тобто враховується

Сім мостів КеніґсберґаНеобхідно було знайти такий маршрут через місто, щоб пройти всі

Леонард Ейлер у 1735 р. довів що розв'язку не існує. Це положило початок створення

Варіація задачіПівнічний берег річки зайнятий замком Синього Принца, південний — Червоного Принца. Східний

Синій Принц проаналізував міські мости з позиції теорії графів і дійшов висновку,

Способи представлення графівІснує два способи представлення графа: у вигляді списку суміжності; у

Матриця суміжностіЦей спосіб є зручним для представлення щільних графів, в яких кількість

Матриця суміжностіДаний спосіб підходить для орієнтованих і неорієнтованих графів. Для неорієнтованих графів

Список суміжностіПідходить для розріджених графів, тобто графів у яких кількість ребер набагато

Список суміжностіПам'ять необхідна для списку суміжності дорівнює O (E + V) що

Пошук в глибинуDepth-first search, DFS - один з методів обходу графа, стратегія якого

Алгоритм пошуку в глибинуПроходимо по всіх вершинах, якщо знаходимо вершину v зафарбовану

Алгоритм пошуку в глибину з часовими міткамиДля кожної з вершин встановимо два

Використовується для вирішення задач:Пошук будь-якого шляху в графі.Перевірка, чи є одна вершина

Пошук в ширинуBreadth-first search, BFS - один з методів обходу графа, працює шляхом

Пошук в ширину (демо)Порядок обходу вершинПроцес обходу графаБілий - вершина, ще не

Алгоритм пошуку в ширинуПомістити вузол, з якого починається пошук, в порожню чергу.Витягти

Використовується для вирішення задач:Пошук найкоротшого шляху в незваженому графі.Пошук компонент зв'язності в

Топологічне сортуванняЦе таке впорядкування вершин направленого графа, що для будь якого ребра

РеалізаціяТопологічне сортування реалізується за допомогою пошуку в глибину, все що необхідно додати

Задача 1Є одяг який треба одягти, і є строго визначений порядок для

Задача легко розв’язується за допомогою потологічного сортування даного графа. Пронумеруємо вершини:0. Нижня

Аналіз розв’язкуНомерами біля вершин позначено час входу/виходу із вершини

Задача 2В останніх маркетингових дослідженнях було виявлено, що цікаві рекламні ролики в

Аналіз розв’язкуЗадача може бути розв’язана пошуком в глибину або в ширину, я

Аналіз розв’язкуМаємо матрицю знайомств в якій m[i][j]=1, якщо i друг j.У першій

Домашнє завдання:Знайти найбільший цикл в графі (найбільший цикл той, що містить максимальну

Слайды презентации

Слайд 2 План лекції
Загальні поняття/теорія
Сім мостів Кеніґсберґа
Способи представлення графів в

задачах
Пошук в глибину
Пошук в ширину
Топологічне сортування
Задача

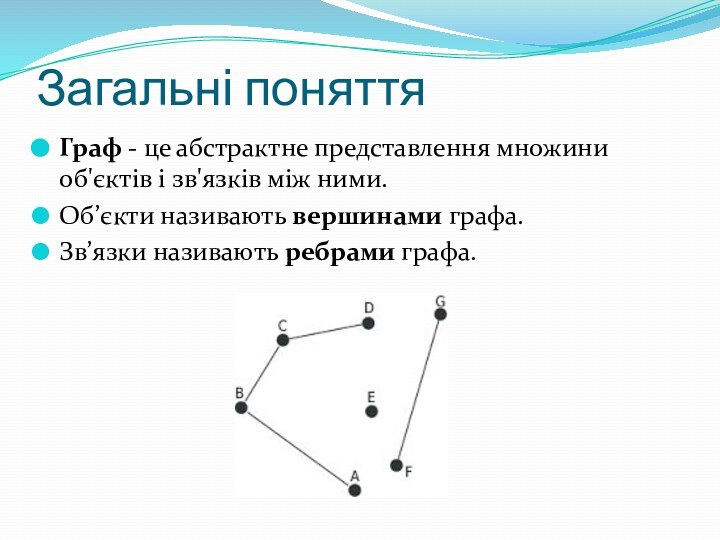
Слайд 3 Загальні поняття
Граф - це абстрактне представлення множини об'єктів

Загальні поняттяГраф - це абстрактне представлення множини об'єктів і зв'язків між

і зв'язків між ними.
Об’єкти називають вершинами графа.
Зв’язки називають ребрами

графа.

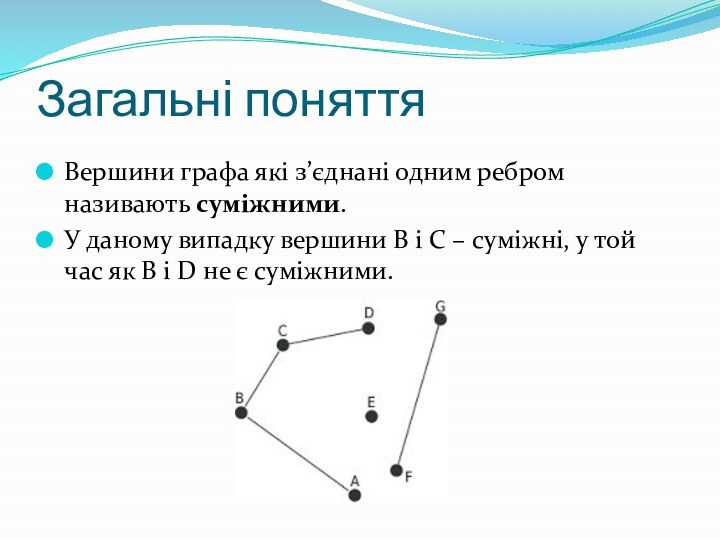
Слайд 4 Загальні поняття
Вершини графа які з’єднані одним ребром називають

суміжними.
У даному випадку вершини B і C – суміжні,

у той час як B і D не є суміжними.

Слайд 5 Загальні поняття
Неорієнтовний граф Орієнтовний граф (орграф)

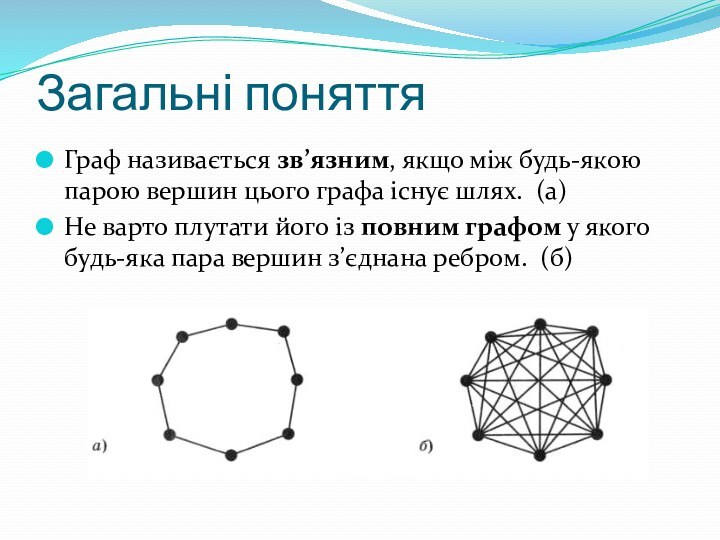
Слайд 6 Загальні поняття
Граф називається зв’язним, якщо між будь-якою парою

Загальні поняттяГраф називається зв’язним, якщо між будь-якою парою вершин цього графа

вершин цього графа існує шлях. (а)
Не варто плутати його

із повним графом у якого будь-яка пара вершин з’єднана ребром. (б)

Слайд 7 Загальні поняття
Дерево – це зв’язний граф без циклів.

Слайд 8 Загальні поняття
Зважений граф – граф який має певну

Загальні поняттяЗважений граф – граф який має певну вагу ребер. Тобто

вагу ребер. Тобто враховується не лише наявність зв’язку між

двома вершинами а й вага цього зв’язку.

Слайд 9 Сім мостів Кеніґсберґа
Необхідно було знайти такий маршрут через

Сім мостів КеніґсберґаНеобхідно було знайти такий маршрут через місто, щоб пройти

місто, щоб пройти всі сім мостів і кожним мостом

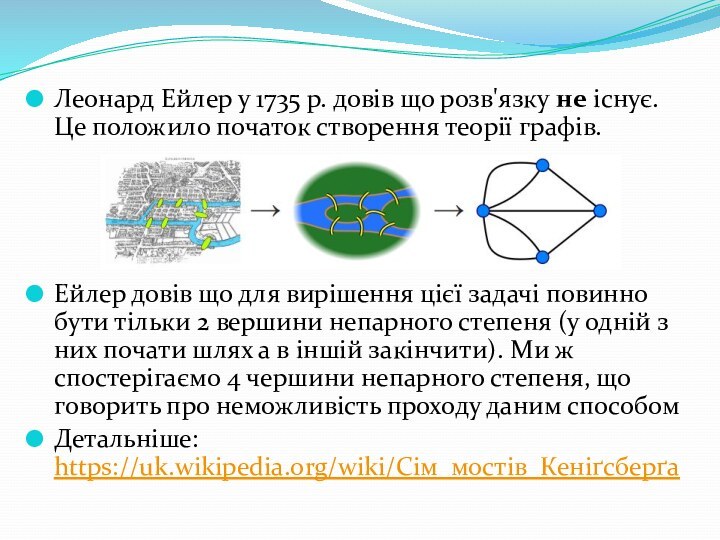
пройти рівно один раз. На острів не можна було потрапити інакше як через міст, і кожен з мостів мав бути пройденим за один раз (тобто не можна було пройти на середину мосту і повернутися назад, а потім з іншого берега пройти другу половину).

Слайд 10 Леонард Ейлер у 1735 р. довів що розв'язку не існує.

Леонард Ейлер у 1735 р. довів що розв'язку не існує. Це положило початок

Це положило початок створення теорії графів.

Ейлер довів що для

вирішення цієї задачі повинно бути тільки 2 вершини непарного степеня (у одній з них почати шлях а в іншій закінчити). Ми ж спостерігаємо 4 чершини непарного степеня, що говорить про неможливість проходу даним способом
Детальніше: https://uk.wikipedia.org/wiki/Сім_мостів_Кеніґсберґа

Слайд 11 Варіація задачі
Північний берег річки зайнятий замком Синього Принца,

Варіація задачіПівнічний берег річки зайнятий замком Синього Принца, південний — Червоного Принца.

південний — Червоного Принца. Східний берег це церква; і маленький

острів це корчма.
Серед місцевих жителів було звичаєм, після кількох годин в корчмі, намагатися обійти мости, багато з них поверталися в корчму, щоб освіжитися для успішного завершення задачі.

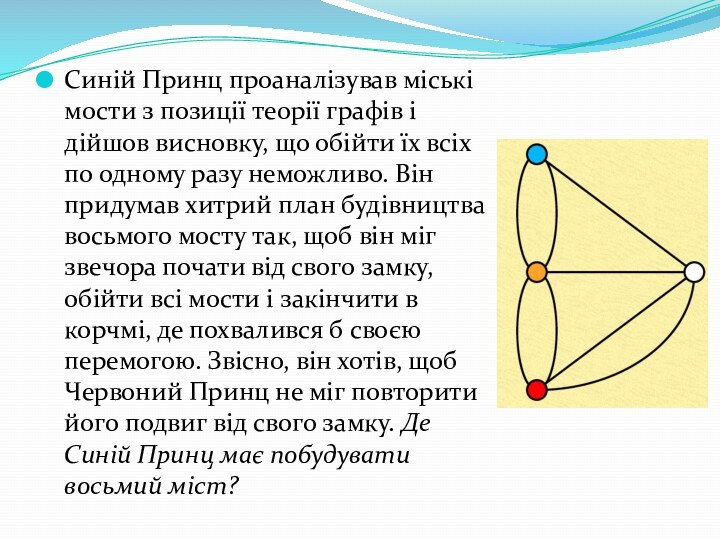
Слайд 12 Синій Принц проаналізував міські мости з позиції теорії

Синій Принц проаналізував міські мости з позиції теорії графів і дійшов

графів і дійшов висновку, що обійти їх всіх по

одному разу неможливо. Він придумав хитрий план будівництва восьмого мосту так, щоб він міг звечора почати від свого замку, обійти всі мости і закінчити в корчмі, де похвалився б своєю перемогою. Звісно, він хотів, щоб Червоний Принц не міг повторити його подвиг від свого замку. Де Синій Принц має побудувати восьмий міст?

Слайд 13 Способи представлення графів
Існує два способи представлення графа:
у

Способи представлення графівІснує два способи представлення графа: у вигляді списку суміжності;

вигляді списку суміжності;
у вигляді матриці суміжності;
Обидва способи підходять

для представлення орієнтованих і неорієнтованих графів.

Слайд 14 Матриця суміжності
Цей спосіб є зручним для представлення щільних

Матриця суміжностіЦей спосіб є зручним для представлення щільних графів, в яких

графів, в яких кількість ребер E приблизно дорівнює кількості

вершин у квадраті V2.
Ми заповнимо матрицю розміром V на V таким чином:
A[i][j] = 1 (Якщо існує ребро з i в j)
A[i][j] = 0 (Інакше)
Можна швидко перевірити чи є ребро між вершинами v і u, просто подивившись в матрицю за адресою A[v][u].

Слайд 15 Матриця суміжності
Даний спосіб підходить для орієнтованих і неорієнтованих

Матриця суміжностіДаний спосіб підходить для орієнтованих і неорієнтованих графів. Для неорієнтованих

графів. Для неорієнтованих графів матриця A є симетричною.

неорієнтований граф орієнтований граф
Недоліком цього способу є великі затрати по пам’яті (матриця вимагає V2 памяті).

Слайд 16 Список суміжності
Підходить для розріджених графів, тобто графів у

Список суміжностіПідходить для розріджених графів, тобто графів у яких кількість ребер

яких кількість ребер набагато менше ніж кількість вершин в

квадраті E << V2 .
В даному представленні використовується масив аdj, що містить V списків. У кожному списку аdj [v] містяться всі вершини u, так що між v і u є ребро.
Іншими словами у списку аdj [v] містяться всі вершини в які ми можемо потрапити із v.

Слайд 17 Список суміжності
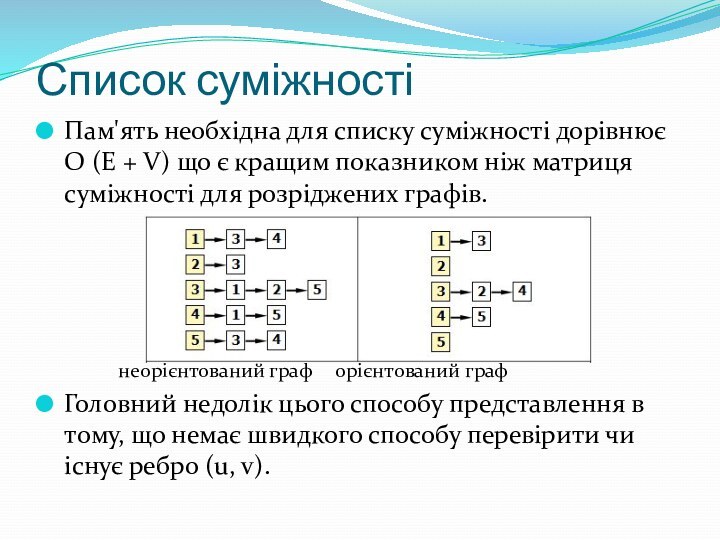
Пам'ять необхідна для списку суміжності дорівнює O

Список суміжностіПам'ять необхідна для списку суміжності дорівнює O (E + V)

(E + V) що є кращим показником ніж матриця

суміжності для розріджених графів.

неорієнтований граф орієнтований граф
Головний недолік цього способу представлення в тому, що немає швидкого способу перевірити чи існує ребро (u, v).

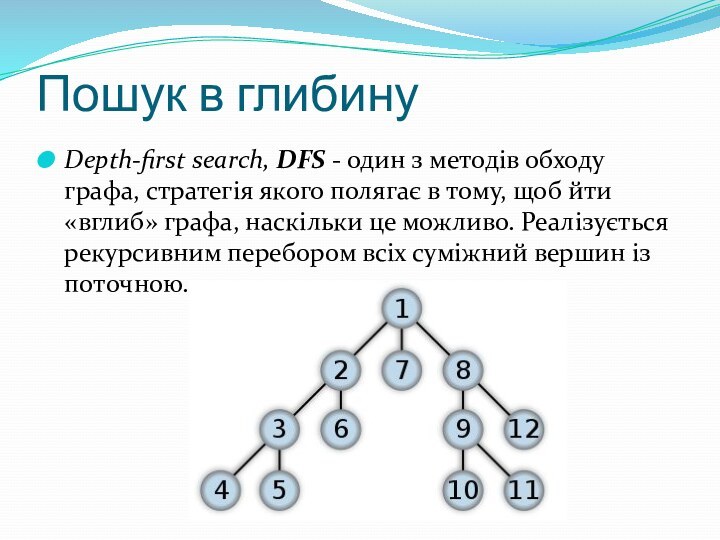
Слайд 18 Пошук в глибину
Depth-first search, DFS - один з методів

Пошук в глибинуDepth-first search, DFS - один з методів обходу графа, стратегія

обходу графа, стратегія якого полягає в тому, щоб йти

«вглиб» графа, наскільки це можливо. Реалізується рекурсивним перебором всіх суміжний вершин із поточною.

Слайд 19 Алгоритм пошуку в глибину
Проходимо по всіх вершинах, якщо

Алгоритм пошуку в глибинуПроходимо по всіх вершинах, якщо знаходимо вершину v

знаходимо вершину v зафарбовану в білий колір запускаємо для

неї DFS(v).
Процедура DFS(v):
Зафарбовуємо v в сірий колір.
Для кожної вершини w, суміжної з v і зафарбованої в білий колір запускаємо DFS(w).
Зафарбовуємо v в чорний колір.
Часто використовують двоколірні мітки - без сірого, тоді на 1-му кроці фарбують відразу в чорний колір.

Слайд 20 Алгоритм пошуку в глибину з часовими мітками
Для кожної

Алгоритм пошуку в глибину з часовими міткамиДля кожної з вершин встановимо

з вершин встановимо два числа: час входу entry[v] та

час виходу з вершини leave[u]. Тоді процедура DFS буде мати такий вигляд:
Збільшуємо «поточний час» t на 1. entry[v] = t.
Зафарбовуємо v в сірий колір.
Для кожної вершини w, суміжної з v і зафарбованої в білий колір запускаємо DFS(w).
Зафарбовуємо v в чорний колір.
Збільшуємо «поточний час» t на 1. leave[v] = t.
Вважаємо, що граф орієнтований, тоді очевидно, для будь-якої вершини entry[v] < leave[v].

Слайд 21 Використовується для вирішення задач:
Пошук будь-якого шляху в графі.
Перевірка,

Використовується для вирішення задач:Пошук будь-якого шляху в графі.Перевірка, чи є одна

чи є одна вершина дерева предком іншої.
Задача LCA (найменший

спільний предок).
Топологічне сортування.
Перевірка графа на ациклічність і знаходження циклу.
Пошук компонент сильної зв'язності.
Пошук мостів.

Алгоритм працює за O (n + m), де n - число вершин, m - число ребер.

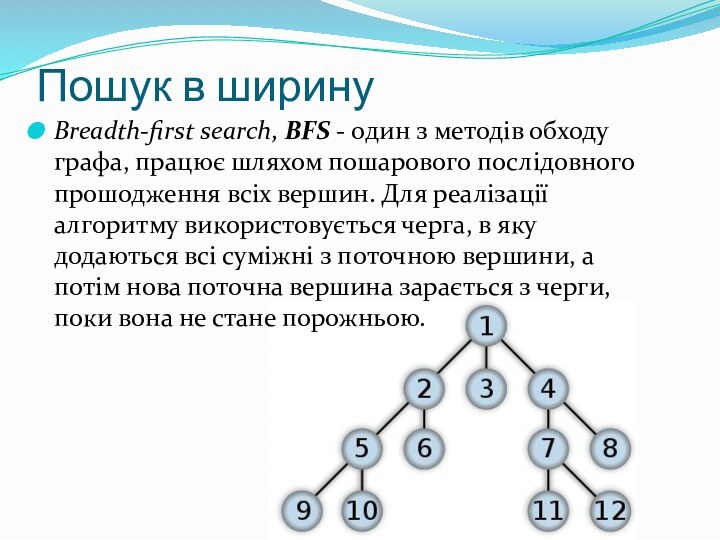
Слайд 22 Пошук в ширину
Breadth-first search, BFS - один з методів

Пошук в ширинуBreadth-first search, BFS - один з методів обходу графа, працює

обходу графа, працює шляхом пошарового послідовного прошодження всіх вершин.

Для реалізації алгоритму використовується черга, в яку додаються всі суміжні з поточною вершини, а потім нова поточна вершина зарається з черги, поки вона не стане порожньою.

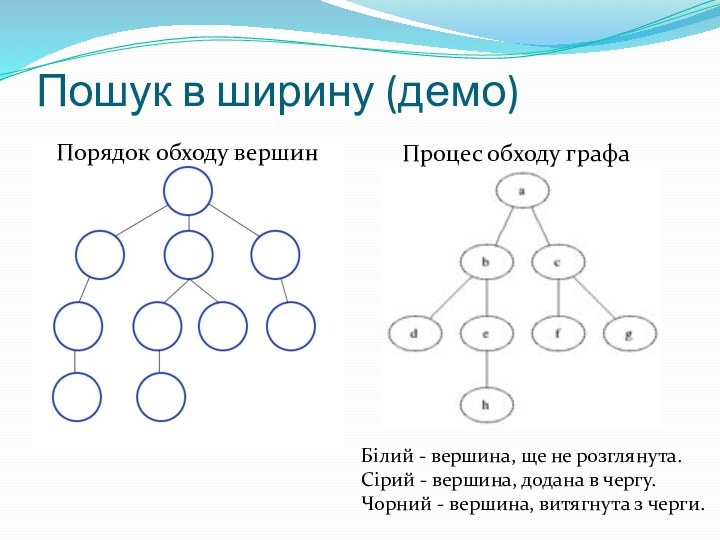
Слайд 23 Пошук в ширину (демо)
Порядок обходу вершин
Процес обходу графа
Білий

Пошук в ширину (демо)Порядок обходу вершинПроцес обходу графаБілий - вершина, ще

- вершина, ще не розглянута.
Сірий - вершина, додана

в чергу.
Чорний - вершина, витягнута з черги.

Слайд 24 Алгоритм пошуку в ширину
Помістити вузол, з якого починається

Алгоритм пошуку в ширинуПомістити вузол, з якого починається пошук, в порожню

пошук, в порожню чергу.
Витягти з початку черги вузол u

і позначити його як відвіданий used[u] = true. Якщо вузол u є цільовим вузлом, то завершити пошук з результатом «успіх». В іншому випадку, в кінець черги додаються всі суміжні з u вершини, які ще не відвідані.
Повернутися до п. 2.
Якщо черга порожня, то всі вузли зв'язкового графа були переглянуті, отже, цільової вузол недосяжний з початкового; пошук завершується з результатом «невдача».

Слайд 25 Використовується для вирішення задач:
Пошук найкоротшого шляху в незваженому

Використовується для вирішення задач:Пошук найкоротшого шляху в незваженому графі.Пошук компонент зв'язності

графі.
Пошук компонент зв'язності в графі за O (n +

m).
Знаходження рішення будь-якої задачі (гри) з найменшим числом ходів (стан гри – вершини а переходи між станами - ребра).
Пошук циклів в графі.
Задачі мінімізації (перестановок, відстаней і т.д.).

Алгоритм працює за O (n + m), де n - число вершин, m - число ребер.

Слайд 26 Топологічне сортування
Це таке впорядкування вершин направленого графа, що

Топологічне сортуванняЦе таке впорядкування вершин направленого графа, що для будь якого

для будь якого ребра (u -> v) вершина u

має бути перед v.
Сортування працює тільки для орієнтованого ациклічного графа.
В результаті сортування графа виходить послідовність, така що всі ребра будуть направлені зліва направо.

Слайд 27 Реалізація
Топологічне сортування реалізується за допомогою пошуку в глибину,

РеалізаціяТопологічне сортування реалізується за допомогою пошуку в глибину, все що необхідно

все що необхідно додати це запис поточної вершини після

виходу із рекурсії.
Якщо використати пошук в глибину с часовими мітками то можна побачити що результуюча послідовність впорядкована по спаданню часу виходу із вершини.

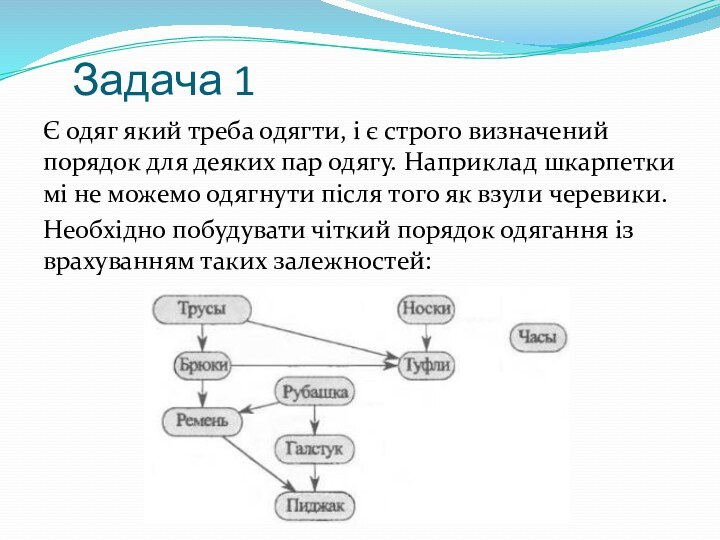
Слайд 28 Задача 1
Є одяг який треба одягти, і є

Задача 1Є одяг який треба одягти, і є строго визначений порядок

строго визначений порядок для деяких пар одягу. Наприклад шкарпетки

мі не можемо одягнути після того як взули черевики.
Необхідно побудувати чіткий порядок одягання із врахуванням таких залежностей:

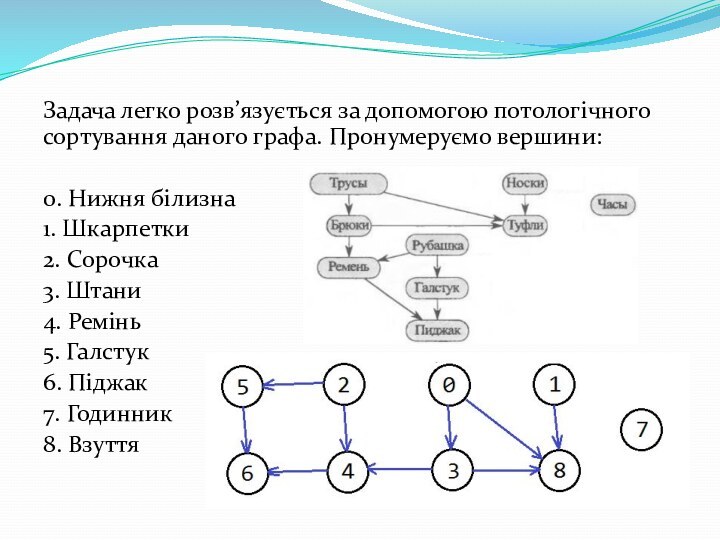
Слайд 29 Задача легко розв’язується за допомогою потологічного сортування даного

Задача легко розв’язується за допомогою потологічного сортування даного графа. Пронумеруємо вершини:0.

графа. Пронумеруємо вершини:

0. Нижня білизна
1. Шкарпетки
2. Сорочка
3. Штани
4. Ремінь
5.

Галстук
6. Піджак
7. Годинник
8. Взуття

Слайд 30 Аналіз розв’язку
Номерами біля вершин позначено час входу/виходу із

вершини

Слайд 31 Задача 2
В останніх маркетингових дослідженнях було виявлено, що

Задача 2В останніх маркетингових дослідженнях було виявлено, що цікаві рекламні ролики

цікаві рекламні ролики в соц. мережах розходяться дуже швидко

між усіма друзями, тому для поширення вірусних роликів в конкретному колі спілкування досить показати цей ролик в стрічці новин соц. мережі одній людині. Такий вид реклами сильно зменшує витрати на її поширення. У маркетологів є дані хто з ким "дружить" в соц. мережі і тепер виникає питання порахувати мінімальну кількість людей, яким необхідно додати вірусний рекламний ролик в новини, щоб він розійшовся по всій мережі.

Слайд 32 Аналіз розв’язку
Задача може бути розв’язана пошуком в глибину

Аналіз розв’язкуЗадача може бути розв’язана пошуком в глибину або в ширину,

або в ширину, я вибираю пошук в ширину. Суть

в тому що ми повинні визначити кількість зв’язних груп у графі, тобто якщо в кожній зв’язній групі одна людина отримає вірусний ролик, то він пошириться на всю мережу(граф).
На вході маємо матрицю знайомств, а на виході маємо дати кількість людей для поширення ролика на всю мережу.

Слайд 33 Аналіз розв’язку
Маємо матрицю знайомств в якій m[i][j]=1, якщо

Аналіз розв’язкуМаємо матрицю знайомств в якій m[i][j]=1, якщо i друг j.У

i друг j.

У першій матриці юзер1 друг з юзером2

а також юзер3 друг з юзером4, тобто маємо
2 незалежні групи людей, що відразу дає
нам відповідь 2.

У другій матриці юзер1 друг з юзер2, юзер2
друг з юзер3, і так далі до юзера 5, отже всі
юзери мережі дружать тому відповідь 1.