Презентация на тему Алгоритмы внутренних точек с приближенным решением вспомогательной задачи

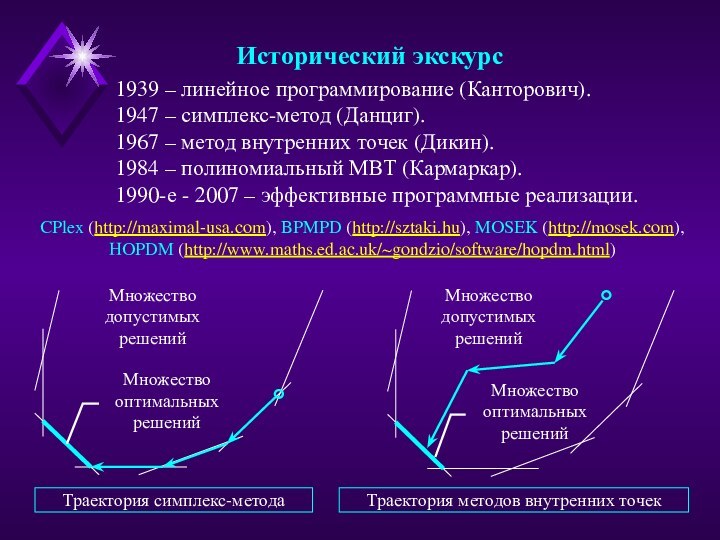
– метод внутренних точек (Дикин).
1984 – полиномиальный МВТ (Кармаркар).
1990-е

CPlex (http://maximal-usa.com), BPMPD (http://sztaki.hu), MOSEK (http://mosek.com),
HOPDM (http://www.maths.ed.ac.uk/~gondzio/software/hopdm.html)

Исторический экскурс

алгоритмы.
Алгоритмы центрального пути.
Алгоритмы скошенного пути.
Комбинированные алгоритмы.

корректировки:
(3)
Способы выбора весовых коэффициентов:
(4)
(5)
(6)
(7)

направления корректировки:
Комбинированные алгоритмы
(используют параметризацию)
(10)
(9)
Задача поиска направления корректировки:

квадратного корня).

Метод сопряженных направлений.
Метод Зейделя.
Другие приближенные

Предпосылки использования
приближенных итеративных методов

На первых итерациях достаточно искать приближенное
направление корректировки , используя вектор ,
для которого .

В финале вычислительного процесса, диагональная мат-
рица изменяется по итерациям очень незначительно,
имеется хорошее стартовое приближение .

корректировки:

n=1,2m
Число итераций, необходимое для решения задач при n=1,5m

параметр в условии останова
δ – параметр в условие

– прогноз шага корректировки.