Слайд 2
Требования к асимметричным системам
(У. Диффи, М. Хеллман)
Вычисление
пары ключей (открытого и закрытого) должно быть простым
Отправитель, зная
открытый ключ Ko легко вычисляет криптограмму C=Eko(M)
Получатель, используя закрытый ключ Kc и криптограмму С легко восстанавливает исходное сообщение M=Dкс(С)
Противник, зная открытый ключ при попытке вычислить секретный наталкивается на непреодолимую проблему
Противник, зная открытый ключ и криптограмму, при попытке восстановить исходное сообщение наталкивается на непреодолимую вычислительную проблему
Слайд 3
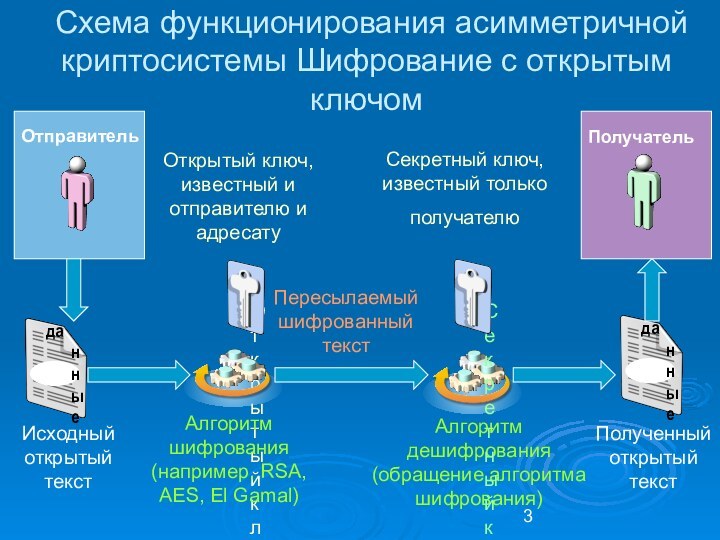
Схема функционирования асимметричной криптосистемы Шифрование с открытым ключом
Отправитель
Открытый
ключ
получателя
Получатель
Секретный ключ получателя
Слайд 4
Однонаправленные функции
Опр: Однонаправленной называется функция F: X?Y, обладающая
свойствами
1) существует полиномиальный алгоритм вычисления F(x)
2) не существует полиномиального
алгоритма инвертирования F (т.е. решения уравнения F(x)=y относительно х)
Слайд 5
Примеры однонаправленных (односторонних функций)
Разложение большого числа на простые
множители N=P*Q,
где Р и Q – простые.
Задача дискретного логарифмирования
Слайд 6
Асимметричные системы шифрования
RSA (Ronald Linn Rivest, Adi Shamir,
Leonard Adleman)
El-Gamal(Шифросистема Эль-Гамаля)
DSA (Digital Signature Algorithm)
Diffie-Hellman (Обмен ключами Диффи — Хелмана)
ECC (Elliptic Curve Cryptography, Системы шифрования основанные на эллиптических кривых)
ГОСТ Р 34.10-2001
Rabin
Luc
McEliece
Williams System (Криптосистема Уильямса)
Слайд 7
Криптосистема RSA (Rivest, Shamir, Adleman)
Открытый текст шифруется блоками,
длиной 2k : 2k
этапов: определение ключей и шифрование/расшифрование
Слайд 8
Алгоритм RSA. Определение ключей
Слайд 9
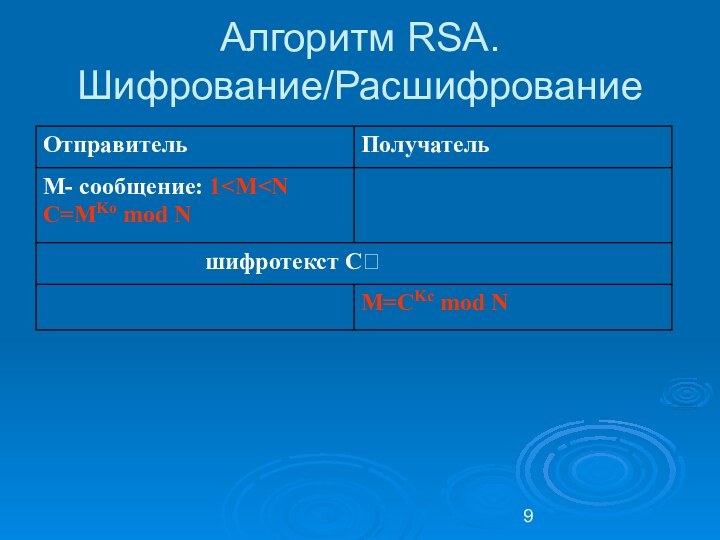
Алгоритм RSA. Шифрование/Расшифрование
Слайд 10
Пример (Получатель)
1. P=5 Q=11
N=5*11=55
φ(N)=(P-1)(Q-1)=4*10=40
Ko: 1
Ko=7
Открытые ключи N=40, Ko=7 ? отправителю
Секретный ключ: Ko*Кc=1 mod
φ(N)
7Kc=1 mod 40
φ(40)= φ(23*5)=(23-22)(51-50)=4*4=16
Kc=716-1*1 mod 40 = 715 mod 40 =
49*49*49*49*49*49*49*7 mod 40 =
9*9*9*9*9*9*9*7 mod 40 = 1*1*1*63 mod 40=23
Kc=23
Слайд 11
Пример (Шифрование)
Отправитель M=6
C=MKo mod N
C=67 mod 55
= 63636 mod 55=
216*216*6 mod 55 =51*51*6 mod 55
=
51*306 mod 55= 51*31 mod 55 = 41
Слайд 12
Пример (Расшифрование)
Получатель С=41
М=CKc mod N = 4123 mod
55 = 412*4121 mod 55 =
31*4121mod 55
=
3111*41 mod 55 =
265*31*41 mod 55 =
162*26*6 mod 55 =
36*46 mod 55 =6
Слайд 13
Технологии, построенные на криптографии с открытым ключом
Распределенная проверка
подлинности (аутентификация)
Коды аутентификации сообщений (Message authentication codes или MAC)
Согласование
общего секретного ключа сессии
Шифрование больших объемов данных без предварительного обмена общим секретным ключом
Электронная цифровая подпись
Слайд 14
Протоколы идентификации и аутентификации
При обмене информацией необходимо выполнять
требования защиты:
Получатель должен быть уверен в подлинности:
-
источника данных;
- данных;
Отправитель должен быть уверен:
- доставке данных получателю;
- подлинности доставленных данных.
Слайд 15
Идентификация и аутентификация
Идентификация – функция системы, которая выполняется
когда объект пытается войти в систему
А – доказывающий
– проходит идентификацию
B – проверяющий – проверяет личность доказывающего
Слайд 16
Идентификация на основе пароля (схема 1)
IDi – идентифицирующая
информация i-го пользователя (напр. ЛОГИН)
Кi – аутентифицирующая информация i-го
пользователя (напр. ПАРОЛЬ)
F – однонаправленная функция
Слайд 17
Идентификация на основе пароля (схема 2)
IDi – идентифицирующая
информация i-го пользователя (ЛОГИН)
Кi – аутентифицирующая информация i-го пользователя
F
– однонаправленная функция
Si – случайная последовательность – «соль»
Слайд 18
Правила составления паролей
Ограничение на минимальную длину (не менее
8 символов)
Наличие различных групп символов (верхний и нижний регистры,
цифры, специальные символы)
Не должен быть словом
Недостатки протоколов с паролем:
А передает секретную информацию (пароль) В
Слайд 19
Протокол идентификации с нулевой передачей знаний
Область применения:
электронные
деньги
системы электронного
голосования
электронные системы
оплаты
Слайд 21
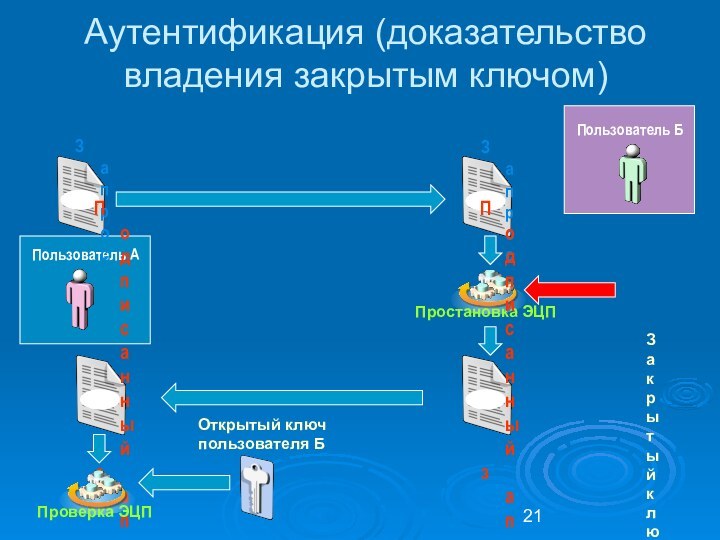
Аутентификация (доказательство владения закрытым ключом)
Закрытый ключ
пользователя Б
Открытый ключ
пользователя
Б
Слайд 22
Пользователь Б
Пользователь A
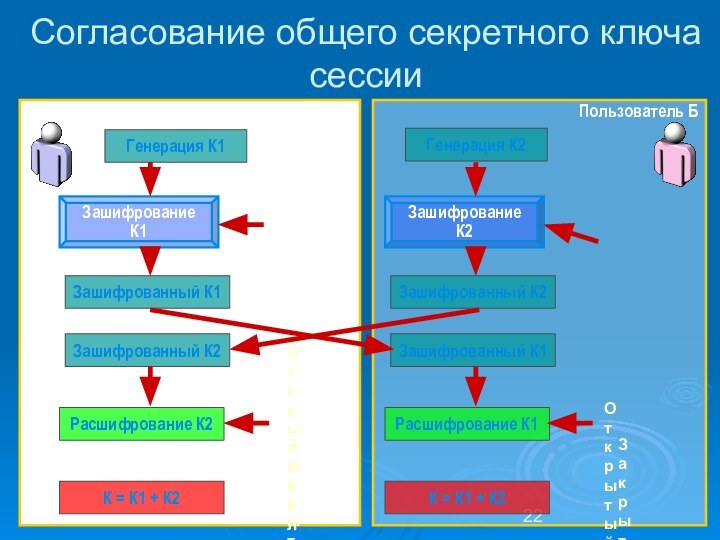
Согласование общего секретного ключа сессии
Генерация К1
Генерация
К2
Зашифрование К1
Открытый ключ
пользователя Б
Зашифрованный К1
Зашифрованный К2
Расшифрование К2
Закрытый ключ
пользователя А
К
= К1 + К2
Зашифрование К2
Открытый ключ
пользователя А
Зашифрованный К2
Зашифрованный К1
Расшифрование К1
Закрытый ключ
пользователя Б
К = К1 + К2
Слайд 23
Протокол передачи ключей.
Прямой обмен ключами Диффи-Хеллмана
Слайд 26
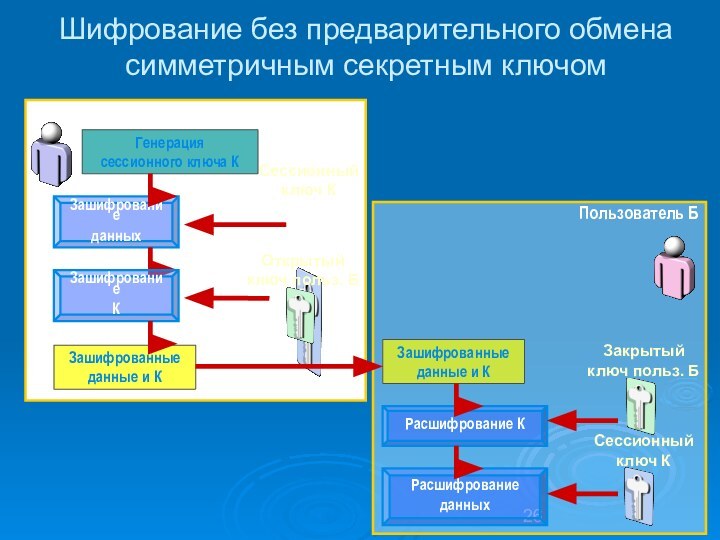
Шифрование без предварительного обмена симметричным секретным ключом
Пользователь Б
Пользователь
A
Генерация
сессионного ключа К
Зашифрование
данных
Сессионный ключ К
Зашифрование
К
Зашифрованные данные
и К
Зашифрованные данные и К
Расшифрование К
Расшифрование
данных
Сессионный ключ К
Слайд 27
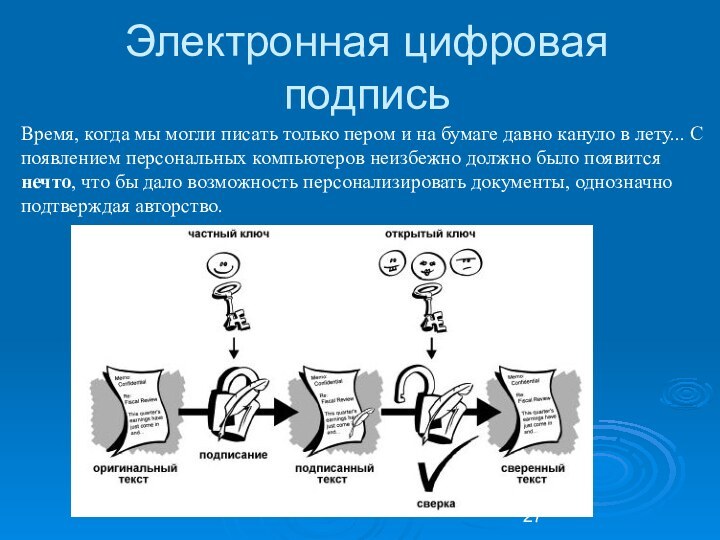
Электронная цифровая подпись
Время, когда мы могли писать только
пером и на бумаге давно кануло в лету... С
появлением персональных компьютеров неизбежно должно было появится нечто, что бы дало возможность персонализировать документы, однозначно подтверждая авторство.
Слайд 28
Электронная цифровая подпись
ЭЦП представляет собой конечную цифровую последовательность,
зависящую от самого сообщения или документа и от некоторого
секретного ключа, известного только подписывающему субъекту.
ЭЦП позволяет решить следующие три задачи:
осуществить аутентификацию источника данных
установить целостность сообщения или электронного документа
обеспечить невозможность отказа от факта подписи
Слайд 29
Алгоритмы ЭЦП
RSA (Ronald Linn Rivest, Adi Shamir, Leonard
Adleman)
DSA (Digital Signature Algorithm)
EC – DSA (вариант
DSA основанный на эллиптических кривых)
Алгоритм подписи Шнорра
Алгоритм подписи Ниберга-Руппеля
и др.
Слайд 30
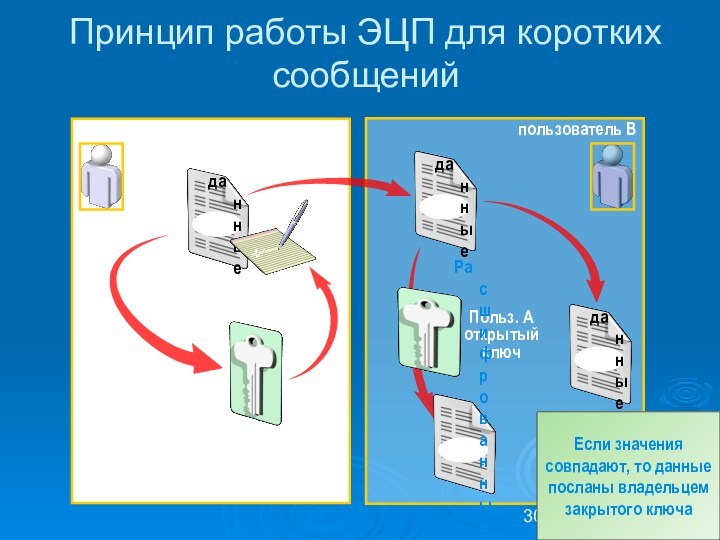
Принцип работы ЭЦП для коротких сообщений
пользователь A
Польз. A
закрытый ключ
Польз. A открытыйключ
Если значения совпадают, то данные посланы
владельцем закрытого ключа
Слайд 31
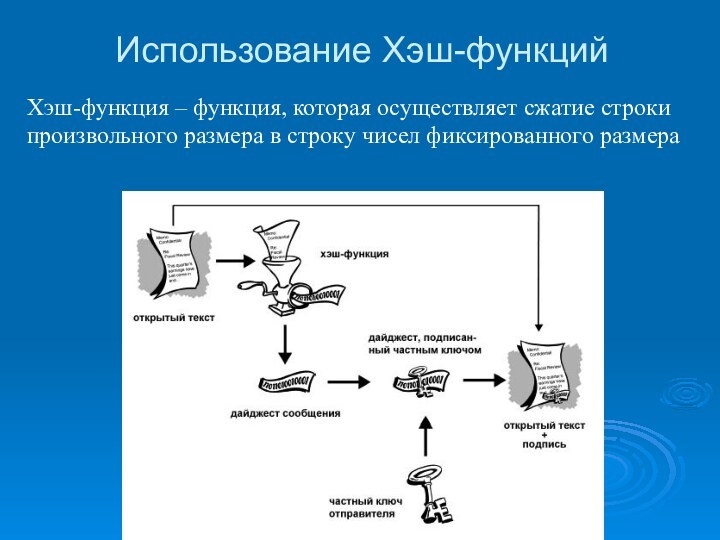
Использование Хэш-функций
Хэш-функция – функция, которая осуществляет сжатие строки
произвольного размера в строку чисел фиксированного размера
Слайд 32
Хеш-функция
Хеширование – математическое однонаправленное преобразование текста в число
фиксированной размерности
Свойства хеш-функции
Свойство лавинности
Свойство стойкости к коллизиям
Свойство необратимости
Алгоритмы, реализующие
хеш-функции
MD4, MD5 (128 бит)
SHA и его варианты SHA1 (160 бит), SHA-256, SHA-512, SHA-384
RIPEMD-160
российский стандарт ГОСТ Р 34.11-94
Слайд 33
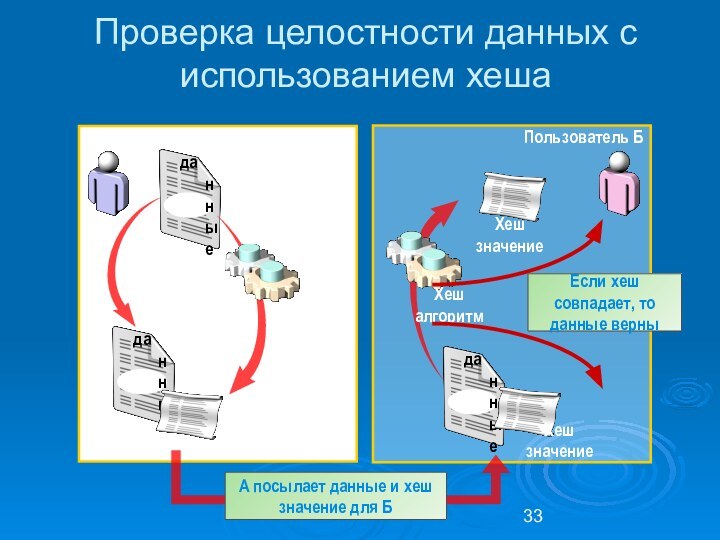
Проверка целостности данных с использованием хеша
Слайд 34
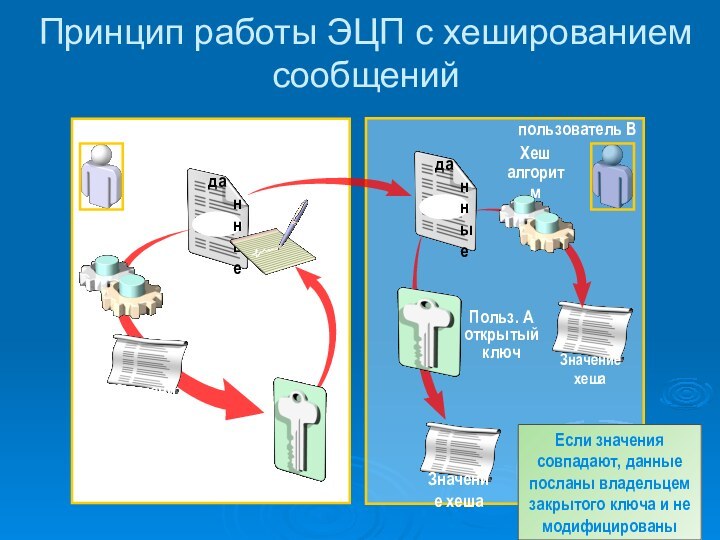
Принцип работы ЭЦП с хешированием сообщений
пользователь A
Польз. A
закрытый ключ
Польз. A открытыйключ
Если значения совпадают, данные посланы владельцем
закрытого ключа и не модифицированы
Слайд 35
Электронная цифровая подпись (на основе RSA)
A сформировал свою
пару секретного (Кс) и открытого(Ко) ключей и на их
основе построил функции Dkс(m) и Eko(m): Eko(Dkс(m))=m
Функция Dkс (m) - функция подписи сообщения m
Функция Eko (m) - функция проверки подписи для сообщения m.
Слайд 36
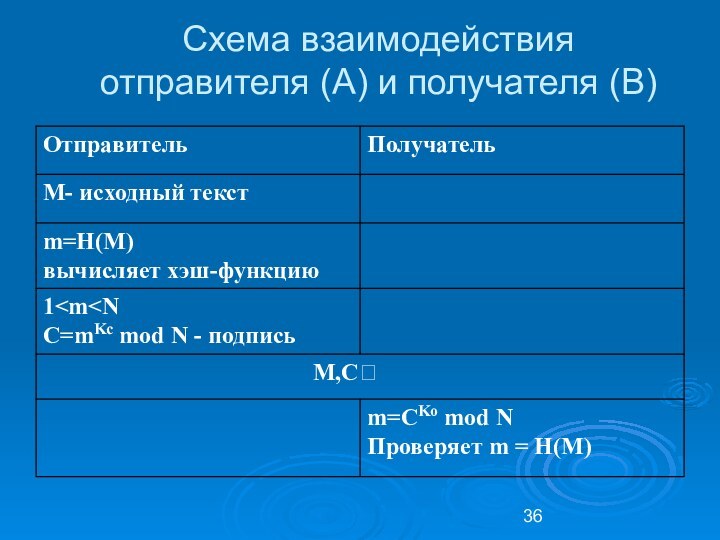
Схема взаимодействия
отправителя (A) и получателя (B)
Слайд 37
Атаки на цифровую подпись
Атаки на алгоритмы (возможные
ошибки в алгоритмах):
Повторение одних и тех же значений алгоритмами
генерации случайных чисел
Возникновение “коллизий” для хеш-функции
Хранение алгоритма в секрете
Атаки на криптосистему
Атаки на реализацию:
Секретный ключ ЭЦП хранится на жестком диске
После завершения работы системы ЭЦП, ключ, хранящийся в оперативной памяти, не затирается
Обеспечивается безопасность сеансовых ключей и недостаточное внимание уделяется защите главных ключей
Отсутствует контроль целостности программы генерации или проверки ЭЦП, что позволяет злоумышленнику подделать подпись или результаты ее проверки
Атаки на пользователя