- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формирование выходных документов на отгружаемую продукцию с помощью сетей Петри
Содержание
- 2. СОДЕРЖАНИЕ1. Общие положения и характеристики ординарных сетей
- 3. Часть 1Общие положения и характеристики ординарных сетей Петри
- 4. ОпределенияОрдинарные сети Петри – тройка множеств C={P,T,E},
- 5. Пример 1: ординарная сеть ПетриПозицииПереходыДуги4321Позиции сети Петри обозначаются кружками, переходы – барьерами(планками), отношения – стрелками (дугами)
- 6. САМОСТОЯТЕЛЬНО1. Граф G(X,U)– это множество вершин X
- 7. Часть 2Использование сетей Петри для поиска оптимальных стратегий формирования документов
- 8. Сети Петри в моделях формирования выходных документов
- 9. Сеть Петри, иллюстрирующая возможные стратегии формирования документовВремя
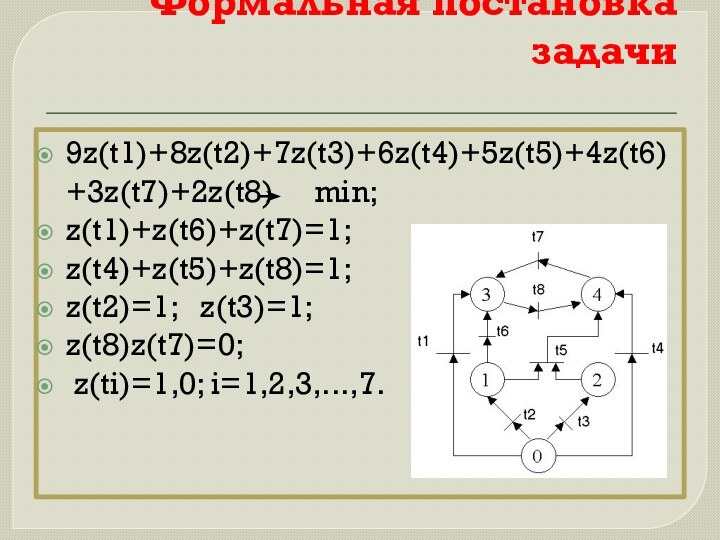
- 10. Формальная постановка задачи9z(t1)+8z(t2)+7z(t3)+6z(t4)+5z(t5)+4z(t6)+3z(t7)+2z(t8) min;z(t1)+z(t6)+z(t7)=1;z(t4)+z(t5)+z(t8)=1;z(t2)=1; z(t3)=1;z(t8)z(t7)=0; z(ti)=1,0; i=1,2,3,...,7.
- 11. Решение задачи переборными алгоритмамиОбъем перебора булевых переменных
- 12. ОбозначенияP’ – подмножество первых i позиций перестановки
- 13. АлгоритмШаг 1. i=1.Шаг 2. Определяется подмножество P’.Шаг
- 14. Пример 2 Пусть π = 1, 2,
- 15. СамостоятельноФормализовать и определить с помощью перестановок оптимальный
- 16. Ответить на вопросыКак построить сеть Петри для
- 17. Часть 3Маркировка и динамика сетей Петри
- 18. Маркировка сети Петри – присвоение позиций числовых
- 19. Выполняется только возбужденный переход, т.е. такой, во
- 20. Пример 1Определить динамику сети Петри применительно к задаче поиска оптимальной стратегии формирования документов
- 21. Начальная позиция выделена красным цветом0
- 22. Расстановка пометок2134А)
- 23. Самостоятельно Определить с помощью расстановки пометок
- 24. СамостоятельноНазовите подсистемы АСУ вуз, которые эквивалентны производственным
- 25. Скачать презентацию
- 26. Похожие презентации
СОДЕРЖАНИЕ1. Общие положения и характеристики ординарных сетей Петри2. Использование сетей Петри для поиска оптимальных стратегий формирования документов3. Маркировка и динамика сетей Петри

















Слайд 2
СОДЕРЖАНИЕ
1. Общие положения и характеристики ординарных сетей Петри
2.
Использование сетей Петри для поиска оптимальных стратегий формирования документов
Маркировка и динамика сетей Петри
Слайд 4
Определения
Ординарные сети Петри – тройка множеств C={P,T,E}, где
Р – множество позиций в сети:
│Р│≠ 0.
Т –
множество переходов:│Т│≠ 0.
Е – отношение инцидентности позиций и переходов т.е. множество дуг сети «С».
Слайд 5
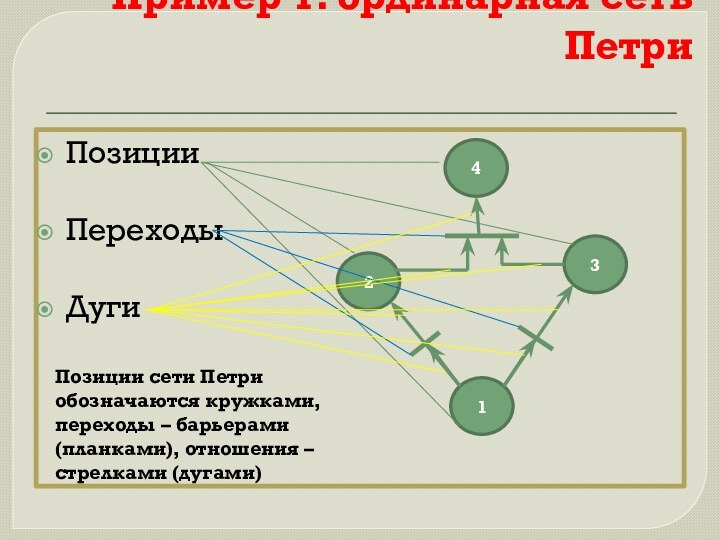
Пример 1: ординарная сеть Петри
Позиции
Переходы
Дуги
4
3
2
1
Позиции сети Петри обозначаются
кружками, переходы – барьерами(планками), отношения – стрелками (дугами)
Слайд 6
САМОСТОЯТЕЛЬНО
1. Граф G(X,U)– это множество вершин X и
отношений их инцидентности U.
2. Сеть Петри - результат развития
теории графов: C={P,T,E} - это множество позиций Р, множество переходов (планок) Т и отношений инцидентности позиций и переходов Е.3. Самостоятельно предложите следующий этап развития теории графов и пример, иллюстрирующий его применение.
Слайд 8
Сети Петри в моделях формирования выходных документов
Содержательная постановка задачи:
Задано множество документов, которые нужно формировать на
основе базы данных и множества программных единиц, которые могут это делать. Каждая единица характеризуется временем и объемом памяти. Каждый документ характеризуется объемом используемой памяти. Требуется построить такую стратегию формирования документов, которая бы:Минимизировала время формирования выходных документов.
Удовлетворяло ограничениям на объем используемой памяти.
Слайд 9
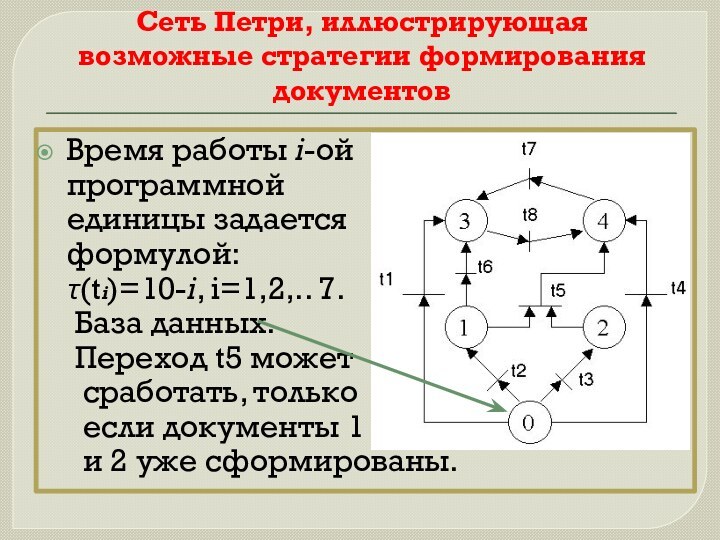
Сеть Петри, иллюстрирующая возможные стратегии формирования документов
Время работы
i-ой
программной
единицы задается
формулой:τ(ti)=10-i, i=1,2,.. 7.
База данных.
Переход t5 может
сработать, только
если документы 1
и 2 уже сформированы.
Слайд 10
Формальная постановка задачи
9z(t1)+8z(t2)+7z(t3)+6z(t4)+5z(t5)+4z(t6)+3z(t7)+2z(t8) min;
z(t1)+z(t6)+z(t7)=1;
z(t4)+z(t5)+z(t8)=1;
z(t2)=1; z(t3)=1;
z(t8)z(t7)=0;
z(ti)=1,0; i=1,2,3,...,7.
Слайд 11
Решение задачи переборными алгоритмами
Объем перебора булевых переменных равен
n1=128.
Объем перебора перестановок вершин n2 = 24.
Объем перебора перестановок
вершин с учетом специфики сети Петри равен n3 = 2.
Слайд 12
Обозначения
P’ – подмножество первых i позиций перестановки π
(│ P’ │= i).
Выбирается k-й переход такой, что:
исходящая из него дуга заходит в позицию, стоящую на (i+1)-м месте в перестановке π;В планку k-го перехода заходят дуги подмножества переходов Т’, в которые заходят только дуги, исходящие из позиций подмножества Р’.
Слайд 13
Алгоритм
Шаг 1. i=1.
Шаг 2. Определяется подмножество P’.
Шаг 3.
Определяется подмножество T’.
Шаг 4. Выбор k-го перехода, для которого
справедливо: Шаг 5. i = i+1.
Шаг 6. Если i>n, то перейти к шагу 7, в противном случае – к шагу 2.
Шаг 7. Конец алгоритма.
Слайд 14
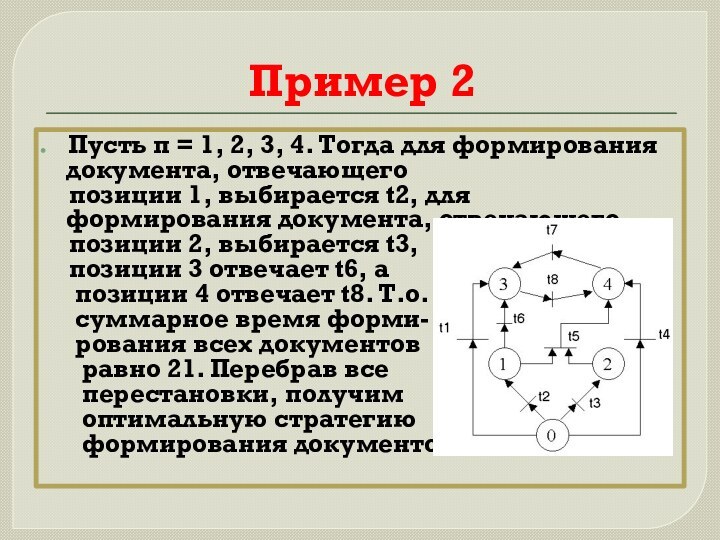
Пример 2
Пусть π = 1, 2, 3,
4. Тогда для формирования документа, отвечающего
позиции 1,
выбирается t2, для формирования документа, отвечающегопозиции 2, выбирается t3,
позиции 3 отвечает t6, а
позиции 4 отвечает t8. Т.о.
суммарное время форми-
рования всех документов
равно 21. Перебрав все
перестановки, получим
оптимальную стратегию
формирования документов.
Слайд 15
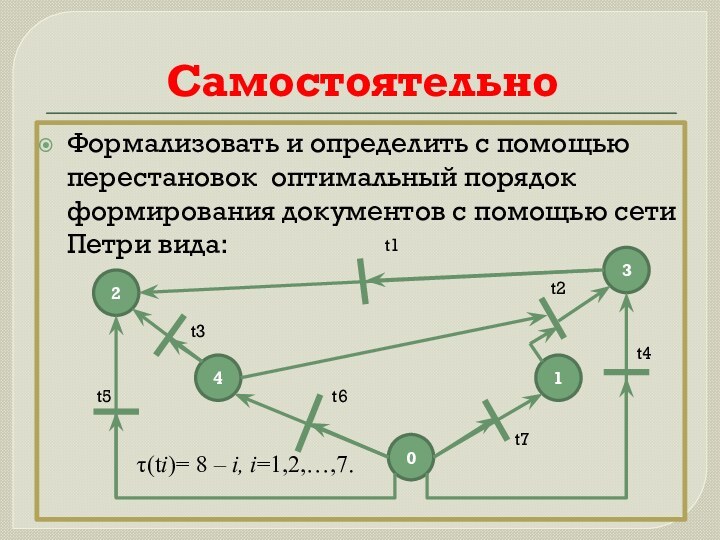
Самостоятельно
Формализовать и определить с помощью перестановок оптимальный порядок
формирования документов с помощью сети Петри вида:
4
2
3
1
0
t1t2
t3
t4
t5 t6
t7
τ(ti)= 8 – i, i=1,2,…,7.
Слайд 16
Ответить на вопросы
Как построить сеть Петри для случая,
когда документы формируются с использованием распределенной базы данных?
Как учесть
в формальной постановке задачи случай, когда в сети Петри существуют контуры? Слайд 18 Маркировка сети Петри – присвоение позиций числовых меток
или значений. Представляется в виде вектора Mj
Динамика сети Петри
определяется соотношением о правилах срабатывания переменных видов.Изменение состояний сети связаны с механизмом изменения маркировок позиций. Приняты следующие правила:
Динамика ординарных сетей Петри.
Слайд 19 Выполняется только возбужденный переход, т.е. такой, во всех
входных позициях которого – 1.
Срабатывание перехода может наступить через
любой конечный промежуток времени, после его возбуждения.Если в каком то состоянии сети Петри возбужденными оказываются несколько переходов, то выполняется только один (любой) из них.
В результате срабатывания перехода, метка меняется в каждой входной его позиции - она уменьшается на 1, а метки во всех его выходных позициях увеличивается на 1.
Выделение перехода – неделимый процесс изменения разметки выполняется мгновенно.
Приняты следующие правила:
Слайд 20
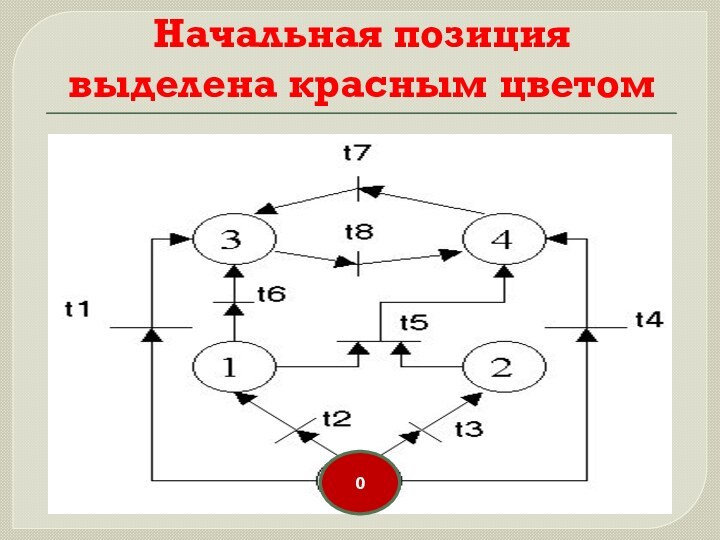
Пример 1
Определить динамику сети Петри применительно к задаче
поиска оптимальной стратегии формирования документов
Слайд 22
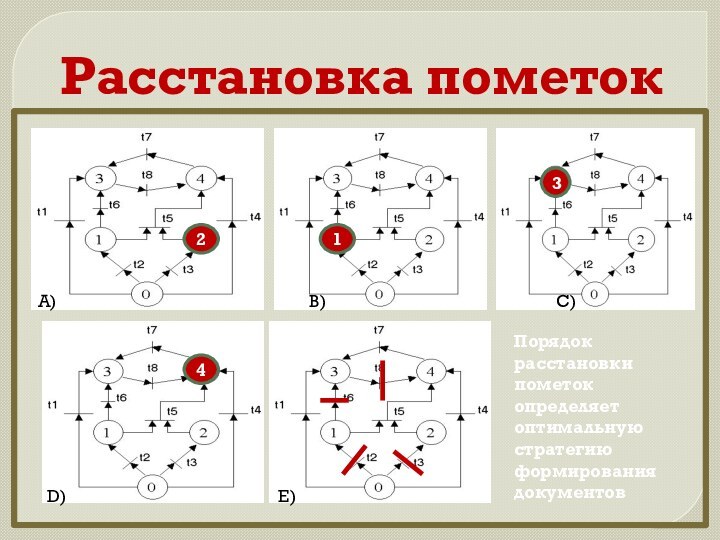
Расстановка пометок
2
1
3
4
А)
В) С)
D) E)
Порядок расстановки пометок определяет оптимальную стратегию формирования документов
Слайд 23
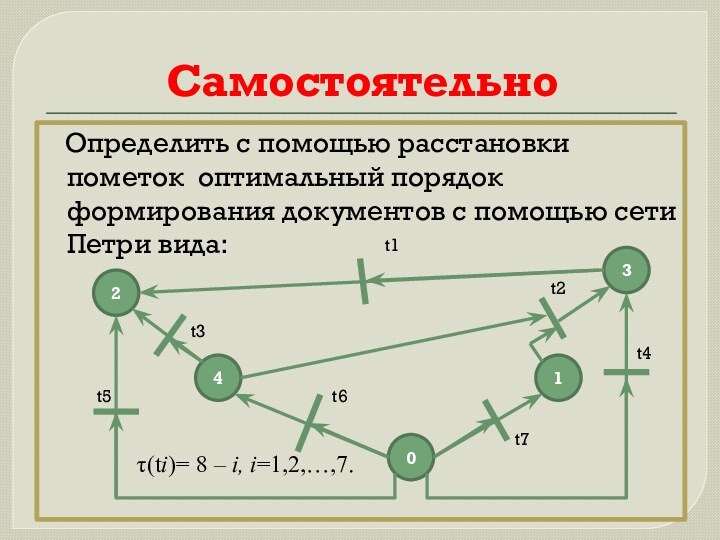
Самостоятельно
Определить с помощью расстановки пометок оптимальный
порядок формирования документов с помощью сети Петри вида:
4
2
3
1
0
t1t2
t3
t4
t5 t6
t7
τ(ti)= 8 – i, i=1,2,…,7.
Слайд 24
Самостоятельно
Назовите подсистемы АСУ вуз, которые эквивалентны производственным подсистемам:
а)
формирования портфеля заказов;
б) технической подготовки производства;
в) управление технологическим процессом;
г)
формирования документов на отгружаемую продукцию;д) логистика (управление запасами).