- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Граф, который построил
Содержание
- 2. Не говори, чему учили, а скажи, что узнал”. (Пословица)
- 3. Граф, который построил...
- 5. Кёнигсберг
- 6. Граф
- 7. Области применения графовмедицинахимия
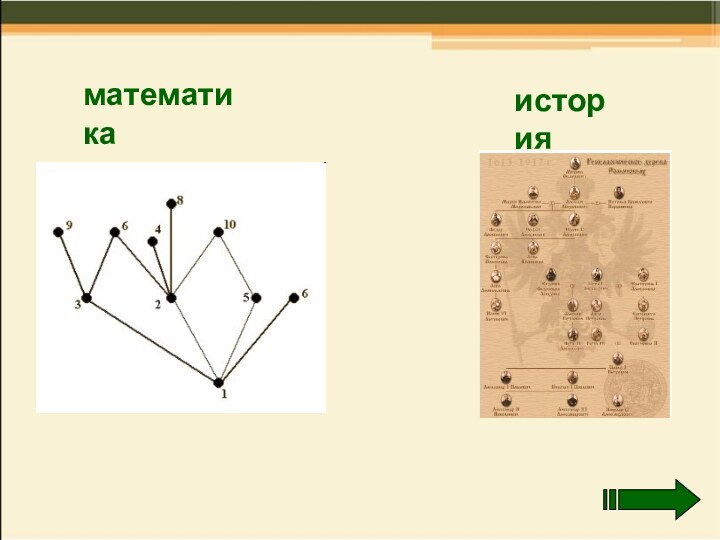
- 8. математикаистория
- 12. ГРАФ - это схема, состоящая из множества
- 13. Из теории графов:Точки графа - вершины.Линия, соединяющая две вершины - ребро.Если линия имеет направление - дуга.
- 14. вершины линия линия дуга - точки графабез стрелкисо стрелкойребро -
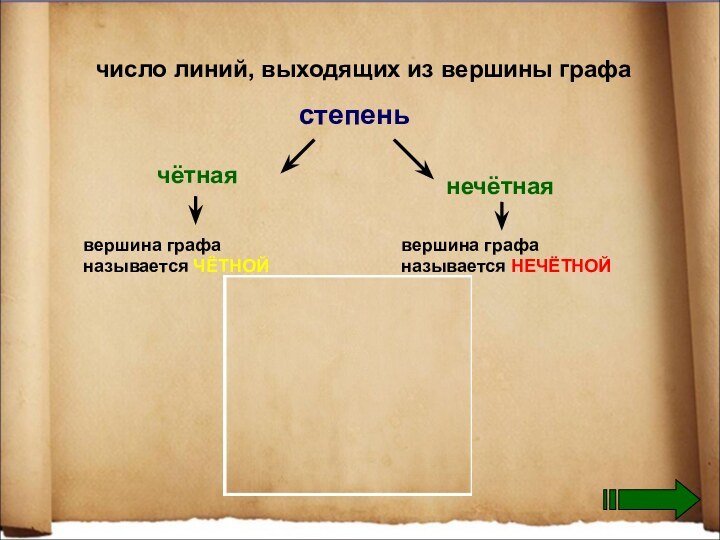
- 15. число линий, выходящих из вершины графастепень вершина графа называется ЧЁТНОЙчётная нечётная вершина графа называется НЕЧЁТНОЙ
- 16. Мы узнали, что такое:граф;вершина, ребро, дуга;степень вершины: чётная, нечётная;
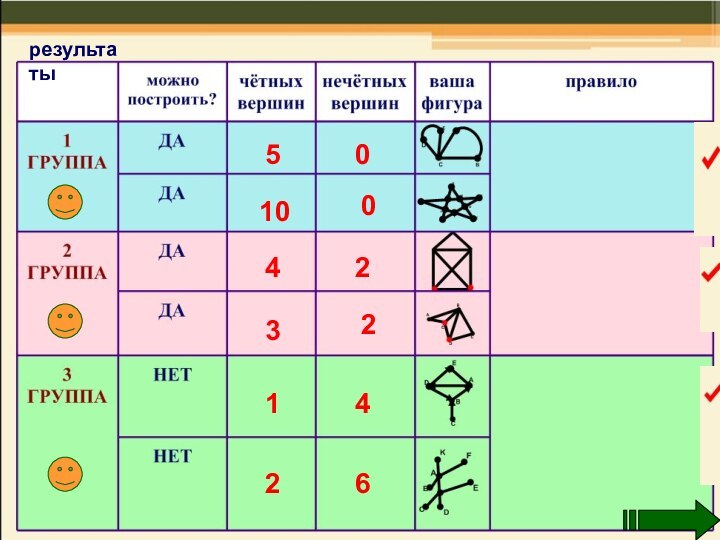
- 17. Граф можно построить если:1) все вершины чётные2)
- 18. результаты 5010042231462
- 19. Задача о мостахне имеет решения!
- 20. Граф, который построил...
- 21. Скачать презентацию
- 22. Похожие презентации
Не говори, чему учили, а скажи, что узнал”. (Пословица)