- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графы
Содержание
- 2. Граф – это конечная совокупность вершин, некоторые
- 3. Виды (примеры) графов:Обычный (неориентированный) граф2 вершины могут
- 4. Ориентированный граф (орграф)- это граф, у которого
- 5. Нагруженный граф - это граф, у которого
- 6. Сеть- это орграф, у которого около каждого
- 7. Решение задачи, моделируемой нагруженным
- 8. Семантический граф- это граф или орграф, у
- 9. Мультиграф2 вершины соединены 2 ребрами и более (кратные ребра)
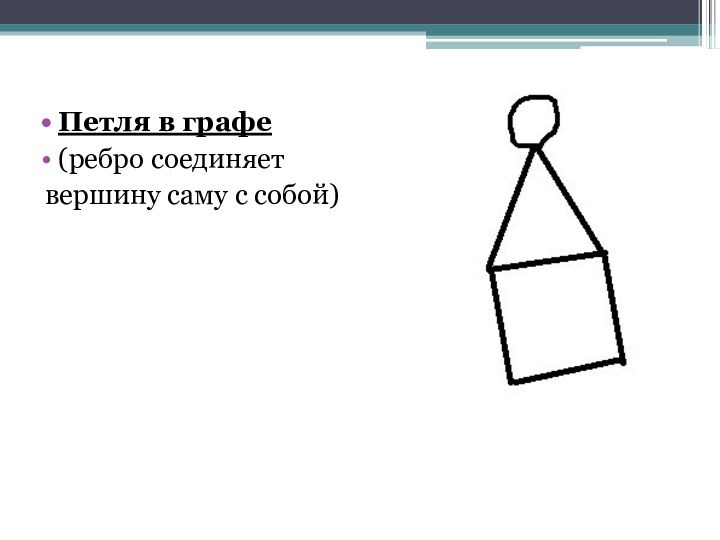
- 10. Петля в графе(ребро соединяет вершину саму с собой)
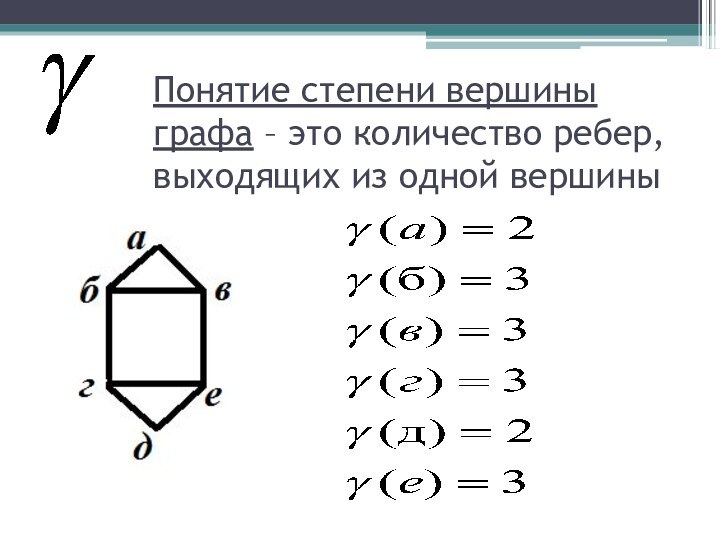
- 11. Понятие степени вершины графа – это количество ребер, выходящих из одной вершины
- 12. СВОЙСТВА ГРАФОВ: 1) Для любого графасумма степеней вершин
- 13. 1) Маршрут на графе – это последовательность
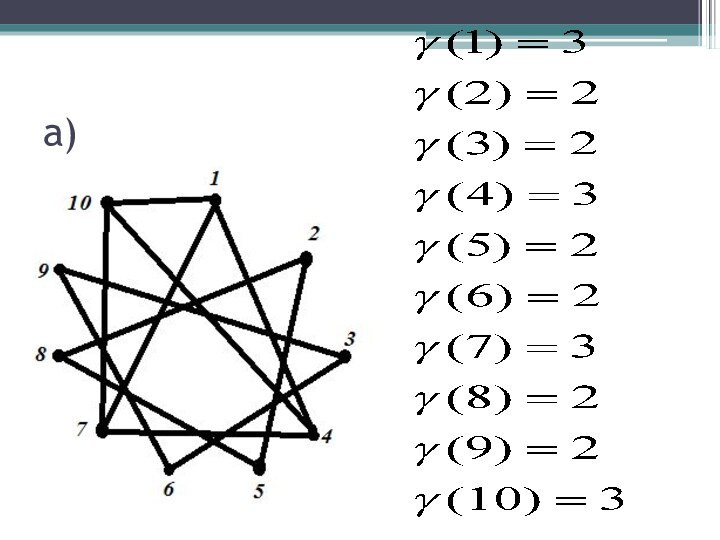
- 14. Пример 1V={1,2,3,4,5,6,7,8,9,10}-это множество вершин графа. Для каждого
- 15. а)
- 16. б)
- 17. в)
- 18. Пример 2: Решение логических задач1) Может ли
- 19. Способы представления графов:1) графический2) табличный (таблица смежности)
- 20. Пример 3Дан граф. Выбрать его табличное представлениеВыбрать его табличное представление:
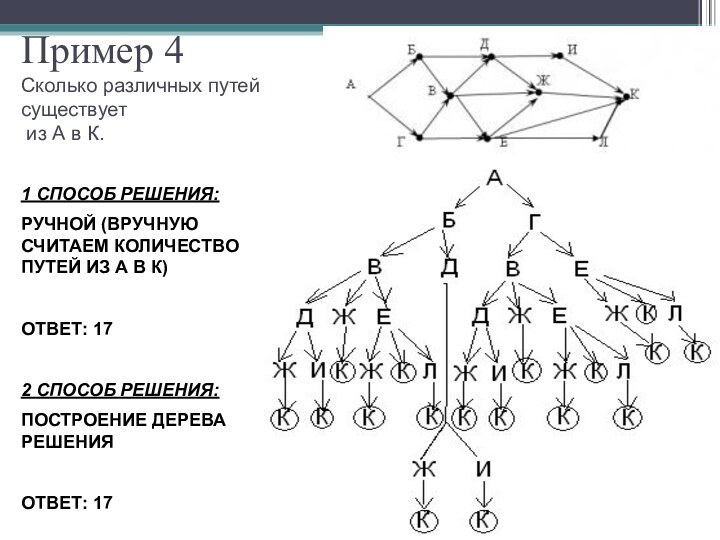
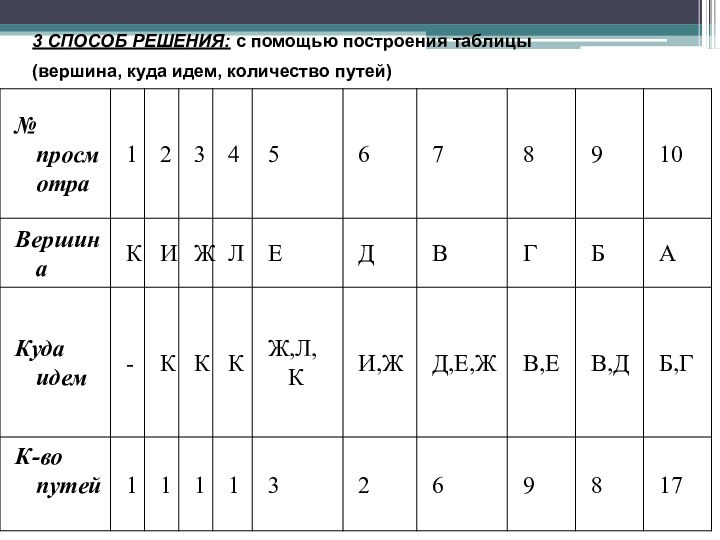
- 21. Пример 4 Сколько различных путей существует
- 22. Скачать презентацию
- 23. Похожие презентации
Граф – это конечная совокупность вершин, некоторые из которых соединены ребрами т.е. это совокупность точек, называемых вершинами, и линий, соединяющих некоторые из вершин, называемых ребрами или дугами в зависимости от вида графа. (н-р, схема метрополитена, генеалогическое















Слайд 3
Виды (примеры) графов:
Обычный (неориентированный) граф
2 вершины могут быть
соединены только одним ребром. Соединяющие линии называются ребрами.
(смежные вершины
– это 2 вершины, соединенные ребром)
Слайд 4
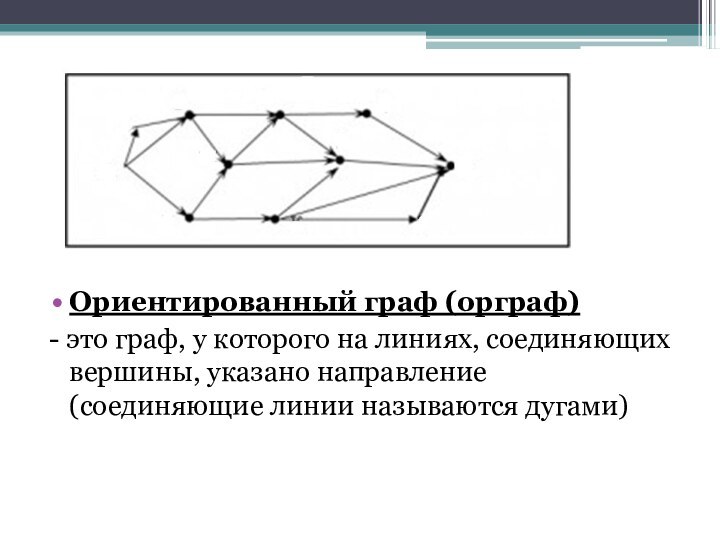
Ориентированный граф (орграф)
- это граф, у которого на
линиях, соединяющих вершины, указано направление (соединяющие линии называются дугами)
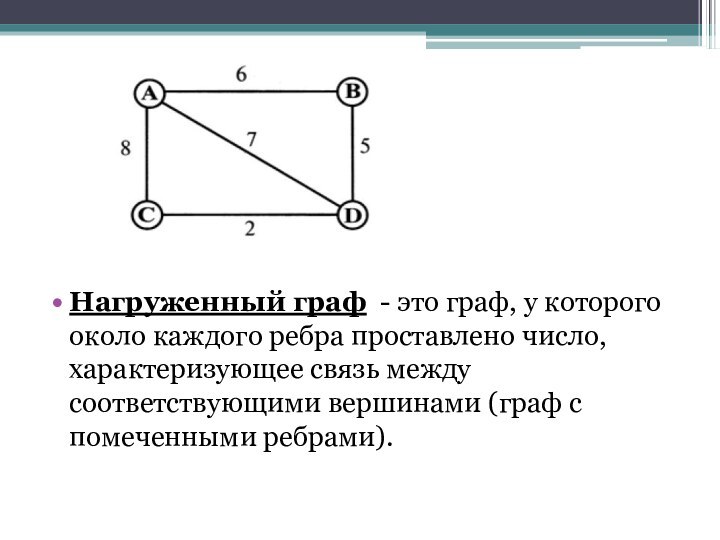
Слайд 5 Нагруженный граф - это граф, у которого около
каждого ребра проставлено число, характеризующее связь между соответствующими вершинами
(граф с помеченными ребрами).Слайд 6 Сеть- это орграф, у которого около каждого ребра
проставлено число, характеризующее связь между соответствующими вершинами (орграф с
помеченными ребрами).Слайд 7 Решение задачи, моделируемой нагруженным графом
или сетью, сводится, как правило, к нахождению оптимального в
том или ином смысле маршрута, ведущего от одной вершины к другойСлайд 8 Семантический граф- это граф или орграф, у которого
около каждого ребра проставлено не число, а иная информация,
характеризующее связь между соответствующими вершинами.
Слайд 12
СВОЙСТВА ГРАФОВ:
1) Для любого графа
сумма степеней вершин равна
удвоенному количеству ребер
2) Для любого графа количество вершин нечетной
степени всегда четно (аналог задачи: в любой момент времени количество людей, сделавших нечетное количество рукопожатий, четно)3) В любом графе есть по крайней мере 2 вершины, имеющие одинаковую степень.
Слайд 13 1) Маршрут на графе – это последовательность ребер,
в которой конец одного ребра служит началом следующего (циклический
маршрут – если конец последнего ребра последовательности совпадает с началом 1-го ребра) 2) Цепь – это маршрут, в котором каждое ребро содержится не более одного раза 3) Цикл – это цепь, являющаяся циклическим маршрутом 4) Простая цепь – это цепь, проходящая через каждую свою вершину ровно 1 раз 5) Простой цикл – это цикл, являющийся простой цепью 6) Связанные вершины – это вершины (например, А и B), для которых существует цепь, начинающаяся в А и заканчивающаяся в B 7) Связный граф – это граф, у которого любые 2 вершины связанны. Если граф несвязен, то в нем можно выделить так называемые связанные компоненты (т.е. множества вершин, соединенных ребрами исходного графа, каждое из которых является связным графом) Один и тот же граф может быть изображен по-разному.
Слайд 14
Пример 1
V={1,2,3,4,5,6,7,8,9,10}-это множество вершин графа. Для каждого из
перечисленных ниже случаев изобразите граф и определите все степени
вершина) вершины x y соединены ребром тогда и только тогда, когда (x-y)/3 целое число
б) вершины x y соединены ребром тогда и только тогда, когда x+y=9
в) вершины x y соединены ребром тогда и только тогда, когда x+y содержится в множестве V={1,2,3,4,5,6,7,8,9,10}
г) вершины x y соединены ребром тогда и только тогда, когда |x-y|<3 (выполнить самостоятельно)
д) вершины x y соединены ребром тогда и только тогда, когда x y не взаимно просты (выполнить самостоятельно)
Слайд 18
Пример 2: Решение логических задач
1) Может ли в
государстве, в котором из каждого города выходят ровно 3
дороги, быть ровно 100 дорог?Ответ: Нет (по формуле 3n=2*100, откуда n-количество городов- не целое)
2) – Наша шпионская сеть была хорошо законспирирована, - признался на допросе агент 007. – В ней было 77 агентов, но каждый знал только семерых. Почему наверняка можно утверждать, что агент врет?
Ответ: По условию задачи 7*77=2*n, откуда n - не целое.
Слайд 21 Пример 4 Сколько различных путей существует из А в
К.
1 СПОСОБ РЕШЕНИЯ:
РУЧНОЙ (ВРУЧНУЮ СЧИТАЕМ КОЛИЧЕСТВО ПУТЕЙ
ИЗ А В К)ОТВЕТ: 17
2 СПОСОБ РЕШЕНИЯ:
ПОСТРОЕНИЕ ДЕРЕВА РЕШЕНИЯ
ОТВЕТ: 17