- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Искусственный интеллект. Эволюционные алгоритмы
Содержание
- 2. Эволюционный поискЭволюционный поиск – это последовательное преобразование
- 3. Особенности АЭВыделяют три особенности алгоритма эволюции (АЭ):1)
- 4. История В конце 1960-х годов американский исследователь
- 5. Основные принципы ГАГенетические алгоритмы (ГА) есть случайно
- 6. Принципы моделирования ГАГенетический алгоритм поиска решения заключается
- 7. Принципы моделирования ГАВ общем случае ГА работает
- 8. Принципы моделирования ГАПопуляция развивается (эволюционирует) от одного
- 9. Принципы моделирования ГАМоделирование процесса мутации новых особей
- 10. Принципы настройки готового ГАК таким параметрам ГА
- 11. Общая схема классического ГАГенерация исходной популяции.Селекция родителей.Кроссинговер
- 12. Генерация исходной популяцииСтратегия "одеяла" – формирование полной
- 13. Отбор родителей (селекция)Пропорциональный отбор (метод "рулетки")Ранжирование Равномерное ранжирование (случайный выбор)Локальный отборОтбор на основе усеченияТурнирный отбор
- 14. Пропорциональный отбор (метод "рулетки")Этот вид отбора чаще
- 15. Пропорциональный отбор (метод "рулетки")- зависимость от положительных
- 16. РанжированиеОсоби популяции сортируются согласно значениям целевой функции.
- 17. Равномерное ранжированиеВероятность выбора особи определяется выражением:где параметр
- 18. Локальный отборПроизводится среди особей, для которых возможно
- 19. Отбор на основе усеченияОтбираемые особи упорядочиваются согласно
- 20. Турнирный отборИз популяции случайно отбираются m особей,
- 21. Отбор родителей из промежуточной группыСлучайный выбор (панмиксия)
- 22. Кроссинговер (скрещивание)Различают два основных вида кроссинговера:
- 23. Двоичная рекомбинацияОдноточечный кроссинговер
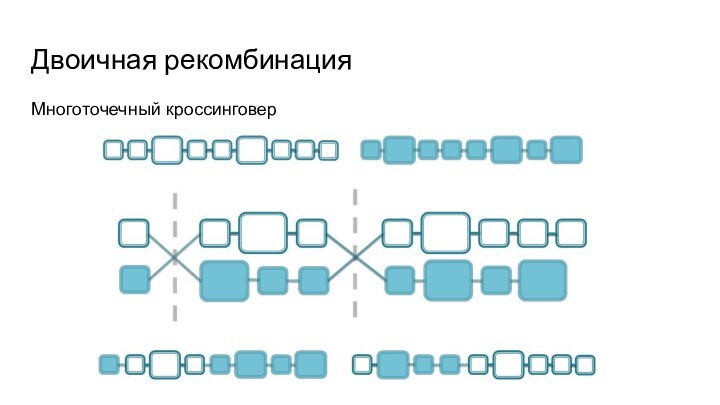
- 24. Двоичная рекомбинацияМноготочечный кроссинговер
- 25. Двоичная рекомбинация:однородный кр-рСлучайным образом генерируется двоичная маска
- 26. Двоичная рекомбинация: ограниченный кр-рТочки скрещивания кроссинговера могут выбираться только там, где значения генов у родителей различны.
- 27. Рекомбинация действительных значенийДискретная рекомбинация: аналогична однородному кроссинговеру,
- 28. Рекомбинация действительных значенийЛинейная рекомбинация аналогична промежуточной рекомбинации
- 29. Понятие “схемы”Понятие «схема» (по Холанду) - это
- 30. Влияние кроссинговера: сохранение схемРассмотрим конкретный стринг длины
- 31. Влияние кроссинговера: сохранение схемСхема Н2 имеет L(H2)
- 32. Влияние кроссинговера: сохранение схемТаким образом, число схем
- 33. Влияние мутации: сохранение схемОператор мутации (ОМ) -
- 34. Влияние кроссинговера и мутации: сохранение схемПоскольку вероятность
- 35. МутацияПосле выполнения оператора скрещивания полученные потомки с
- 36. МутацияДвоичная мутация:1) Классическая мутация: замена случайно выбранного
- 37. Сокращение промежуточной популяцииГлобальная редукция - промежуточную популяцию
- 38. Чистая замена и Элитарная схема В простейшем
- 39. Равномерная случайная замена и пропорциональная редукцияПри равномерной
- 40. Селекционная схемаРодители и потомки выступают на равных
- 41. Локальная заменаРодитель особи определяются первым родителем из
- 42. ГА с изменяемой мощностью популяцииЕсли мощность популяции
- 43. Структура ГА с изменяемой мощностью популяцииИнициализация начальной
- 44. ГА с изменяемой мощностью популяцииСрок жизни для
- 45. Стратегии определения срока жизни особи1) Пропорциональный метод
- 46. Пропорциональный метод определения срока жизниСрок жизни определяется
- 47. Линейный способ определения срока жизни особиСрок жизни
- 48. Билинейный способ определения срока жизни особиСрок жизни
- 49. Пример решения задачиРассмотрим следующий пример, в котором
- 50. Порядок решения задачиСоздание исходной популяции: приемлемые варианты.Аргументация
- 51. Пример внешнего вида UI реализации
- 52. Скачать презентацию
- 53. Похожие презентации
Эволюционный поискЭволюционный поиск – это последовательное преобразование одного конечного множества промежуточных решений в другое. Основой для его возникновения считается модель биологической эволюции и методы случайного поиска. Эволюционный процесс представляется как способность “лучших” хромосом оказывать большее влияние















































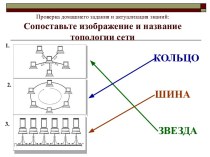
Слайд 2
Эволюционный поиск
Эволюционный поиск – это последовательное преобразование одного
конечного множества промежуточных решений в другое.
возникновения считается модель биологической эволюции и методы случайного поиска. Эволюционный процесс представляется как способность “лучших” хромосом оказывать большее влияние на состав новой популяции на основе длительного выживания и более многочисленного потомства. Само преобразование можно назвать алгоритмом поиска, или алгоритмом эволюции.
Слайд 3
Особенности АЭ
Выделяют три особенности алгоритма эволюции (АЭ):
1) каждая
новая популяция, состоит только из «жизнеспособных» хромосом;
2) каждая новая
популяция «лучше» (в смысле близости к решению поставленной задачи) предыдущей;3) в процессе эволюции последующая популяция зависит только от предыдущей.
Слайд 4
История
В конце 1960-х годов американский исследователь Джон
Холланд предложил в качестве механизма комбинаторного перебора вариантов решения
оптимизационных задач использовать методы и модели механизмов развития (эволюционирования) органического мира на Земле.1962 год, работа «Outline for a logical theory of adaptive systems», in: JACM, Vol 9, nr. 3, pp. 279—314.
Слайд 5
Основные принципы ГА
Генетические алгоритмы (ГА) есть случайно направленные
поисковые алгоритмы, основанные на механизмах естественной селекции и натуральной
генетики. Они реализуют принцип «выживание сильнейших» среди рассматриваемых структур, формируя и изменяя поисковый алгоритм на основе моделирования эволюции.Они основаны на следующих механизмах естественной эволюции:
1) Первый принцип основан на концепции выживания сильнейших и естественного отбора.
2) Второй принцип обусловлен тем фактом, что хромосома потомка состоит из частей полученных из хромосом родителей.
3) Третий принцип основан на концепции мутации.
Слайд 6
Принципы моделирования ГА
Генетический алгоритм поиска решения заключается в
моделировании эволюционирования подобной искусственной популяции.
В ГА из всего пространства
поиска выделяется некоторое множество точек этого пространства (потенциальных решений), которое в терминах натуральной селекции и генетики называется популяцией. Каждая особь популяции – потенциальное решение задачи, представляется хромосомой – структурой элементов – генов.
В свою очередь, произвольный ген хромосомы принимает значение – аллель, из некоторого алфавита, задающего кодовое представление точек пространства поиска решений.
Слайд 7
Принципы моделирования ГА
В общем случае ГА работает с
кодированными структурами безотносительно их смысловой интерпретации.
Сам код и
его структура описываются понятием генотип, а его интерпретация, с точки зрения решаемой задачи, понятием фенотип. На множестве решений определяется целевая (fitness) функция (ЦФ), которая позволяет оценить близость каждой особи к оптимальному решению – способность к выживанию.
Слайд 8
Принципы моделирования ГА
Популяция развивается (эволюционирует) от одного поколения
к другому. Создание новых особей в процессе работы алгоритма
происходит на основе моделирования процесса размножения.При этом особи-решения, участвующие в процессе воспроизводства называют родителями, а получившиеся в результате особи-решения – потомками.
Непосредственная генерация новых кодовых значений особей из двух выбранных происходит за счет применения оператора кроссинговера (скрещивания).
Слайд 9
Принципы моделирования ГА
Моделирование процесса мутации новых особей осуществляется
за счет применения оператора мутации, которые позволяют внести в
фенотип потомка свойства (которые потомок не мог унаследовать от родителей) путем некоторых изменений его генотипа.В общем случае, мутация носит случайный характер, это стойкое (то есть такое, которое может быть унаследовано потомками данной клетки или организма) преобразование генотипа.
Слайд 10
Принципы настройки готового ГА
К таким параметрам ГА относятся:
размер популяции, набор генетических операторов, задействованных в алгоритме и
вероятности их использования, критерий остановки процесса поиска.Критерием остановки может быть:
1) прохождение определенного числа поколений;
2) достижение требуемого качества решений
3) отсутствие улучшения качества решений из-за вырождения текущей популяции.
Слайд 11
Общая схема классического ГА
Генерация исходной популяции.
Селекция родителей.
Кроссинговер (скрещивание).
Мутация.
Объединение
популяций и редукция.
Проверка критерия остановки алгоритма, и в зависимости
от результата:перейти к шагу 2, либо сохранить лучшую особь текущей популяции.
Слайд 12
Генерация исходной популяции
Стратегия "одеяла" – формирование полной популяции,
содержащей все возможные решения. Например, для n-разрядной хромосомы мы
имеем всего 2n вариантов решений, которые составляют полную популяцию.Стратегия "дробовика" - генерация достаточно большого случайного подмножества решений.
Стратегия фокусировки - генерация множества решений, включающих разновидности одного решения.
Слайд 13
Отбор родителей (селекция)
Пропорциональный отбор (метод "рулетки")
Ранжирование
Равномерное
ранжирование (случайный выбор)
Локальный отбор
Отбор на основе усечения
Турнирный отбор
Слайд 14
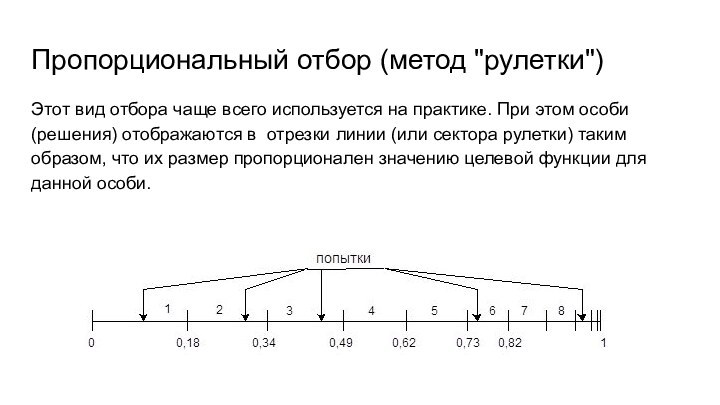
Пропорциональный отбор (метод "рулетки")
Этот вид отбора чаще всего
используется на практике. При этом особи (решения) отображаются в
отрезки линии (или сектора рулетки) таким образом, что их размер пропорционален значению целевой функции для данной особи.
Слайд 15
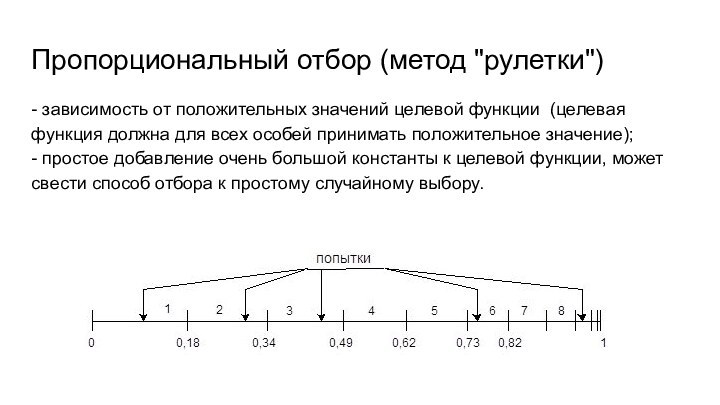
Пропорциональный отбор (метод "рулетки")
- зависимость от положительных значений
целевой функции (целевая функция должна для всех особей принимать
положительное значение);- простое добавление очень большой константы к целевой функции, может свести способ отбора к простому случайному выбору.
Слайд 16
Ранжирование
Особи популяции сортируются согласно значениям целевой функции. Отметим,
что здесь вероятность отбора для каждой особи зависит только
от ее номера в списке, а не от самого значения целевой функции. Этот метод отбора более устойчив, чем предыдущий. В основном, применяют линейное ранжирование, где вероятность отбора определяют в соответствии с выражением.где 1<а<2 выбирается случайным образом,b=2-a ,N – мощность популяции, i – номер особи.
Слайд 17
Равномерное ранжирование
Вероятность выбора особи определяется выражением:
где параметр
определяет какие особи не будут
рассматриваться.
Слайд 18
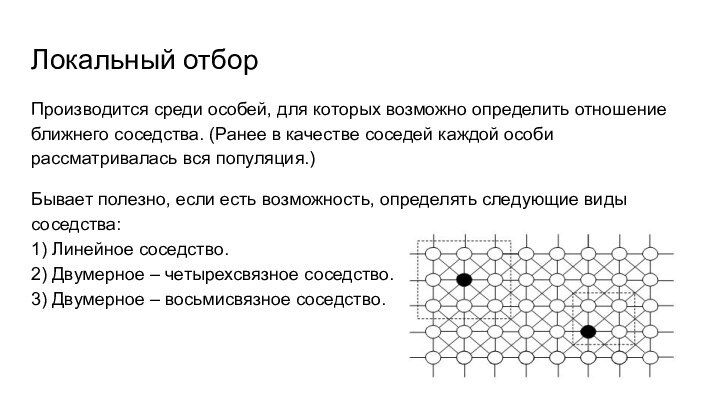
Локальный отбор
Производится среди особей, для которых возможно определить
отношение ближнего соседства. (Ранее в качестве соседей каждой особи
рассматривалась вся популяция.)Бывает полезно, если есть возможность, определять следующие виды соседства:
1) Линейное соседство.
2) Двумерное – четырехсвязное соседство.
3) Двумерное – восьмисвязное соседство.
Слайд 19
Отбор на основе усечения
Отбираемые особи упорядочиваются согласно их
значениям целевой функции.
В качестве родителей выбираются только лучшие
особи. С равной вероятностью, среди них случайно выбирают пары которые производят потомков.
Слайд 20
Турнирный отбор
Из популяции случайно отбираются m особей, и
лучшая из них выбирается в качестве родителя.
Процесс повторяется,
пока не сформируется промежуточная популяция, в которой случайно формируются пары родителей. Параметром турнирного отбора является размер турнирной группы m, который принимает значения из диапазона 2
Слайд 21
Отбор родителей из промежуточной группы
Случайный выбор (панмиксия) родительской
пары, при котором оба родителя случайным образом выбираются из
текущей грппы.Селективный выбор. Здесь родителями могут стать только те особи, значение целевой функции которых не меньше среднего значения по популяции при равной вероятности этих кандидатов.
Могут использоваться также два следующих подхода: инбридинг и аутбридинг. В них формирование пары происходит на основе близкого или дальнего родства соответственно. Под родством обычно понимается расстояние между особями популяции в пространстве параметров.
Слайд 22
Кроссинговер (скрещивание)
Различают два основных вида кроссинговера:
“Двоичная”
рекомбинация:
1) Одноточечный кроссинговер
2) Многоточечный кроссинговер
3) Однородный кроссинговер
4) Ограниченный кроссинговер
Рекомбинация действительных значений:
1) Дискретная рекомбинация
2) Промежуточная рекомбинация
3) Линейная рекомбинация
Слайд 25
Двоичная рекомбинация:однородный кр-р
Случайным образом генерируется двоичная маска кроссинговера
той же длины. Маска задаёт какой из генов берётся
из какого родителя.Т.е. каждый ген потомка создается путем копирования соответствующего гена из первого или второго родителя, каждая позиция потенциально является точкой кроссинговера.
Слайд 26
Двоичная рекомбинация: ограниченный кр-р
Точки скрещивания кроссинговера могут выбираться
только там, где значения генов у родителей различны.
Слайд 27
Рекомбинация действительных значений
Дискретная рекомбинация: аналогична однородному кроссинговеру, только
подразумевается, что генами являются числа.
Промежуточная рекомбинация: применима для особей,
представленных вещественными значениями. Здесь значения потомков строятся в окрестности или между значениями родителей.где P – вещественные значения, представляющие первого и второго родителя; Of – вещественное значение, представляющее потомка;
- масштабирующий множитель, который выбирается случайно из отрезка [-d, 1+ d]. Для обычной промежуточной рекомбинации d=0. Для обобщенной промежуточной рекомбинации d=0,25 .
Слайд 28
Рекомбинация действительных значений
Линейная рекомбинация аналогична промежуточной рекомбинации с
тем только отличием, что коэффициент выбирается для генерируется
для кажого гена отдельно. В случае промежуточной рекомбенации коэффициент одинаков для всех генов хромосомы.
Слайд 29
Понятие “схемы”
Понятие «схема» (по Холанду) - это шаблон,
описывающий подмножество стрингов, имеющих одинаковые значения в некоторых позициях.
Для этого вводится новый троичный алфавит {0, 1, *}, где * означает неопределенное значение (0 или 1, то неизвестно что именно). Например, схема (0*0001) соответствует двум стрингам {000001, 010001}, а (*0110*) описывает подмножество из 4-х стрингов {00100, 101100, 001101, 101101}.Схема с m неопределенными позициями “*” представляет 2m стрингов. Для стрингов длины n, существует 3n схем (возможны 3 символа {0, 1, *} в каждой из n позиций).
Слайд 30
Влияние кроссинговера: сохранение схем
Рассмотрим конкретный стринг длины n
= 7 А = 011| 1000 и две
схемы, представляющие этот стринг:H1 = *1*| ***0, H2 = ***| 10**.
Символ ‘|’ обозначает точку кроссинговера (k=4).
Схема Н1 после ОК в точке k=4, скорее всего, будет уничтожена потому, что ‘1’ в позиции 2 и ‘0’ в позиции 7 попадут в разные новые стринги после кроссинговера. С другой стороны, ясно, что схема Н2 будет чаще “выживать”.
Схема Н1 менее приспособлена к выживанию, чем схема Н2. Если точка скрещивания ОК выбирается случайно среди n-1 = 7-1 = 6 возможных позиций, то схема Н1 разрушается с вероятностью: P(d) = L(H1) / (L-1) = ⅚,
выживает с вероятностью: P(S) = 1-P(d) = 1/6.
Слайд 31
Влияние кроссинговера: сохранение схем
Схема Н2 имеет L(H2) =
1 и вероятность её уничтожения P(d) = 1/6, а
вероятность сохранения схемы после применения ОК P(S) = 5/6.Вероятность выживания для простого ОК может быть вычислена для любой схемы по формуле:
Ps(OK) = 1 – L(H)/(L-1).
Если ОК выполняется с вероятностью РОК, то вероятность выживания схемы определяется:
P(S) >= 1 – РОК*L(Р)/(L-1).
При независимости выполнения ОР и ОК можно получить следующее выражение:
Слайд 32
Влияние кроссинговера: сохранение схем
Таким образом, число схем Н
в новой популяции зависит от двух факторов:
1) значение ЦФ
схемы выше или ниже ЦФ популяции;2) схема имеет “длинную” или “короткую” L(H) (определенную длину).
Cхемы со значением ЦФ выше средней и короткой длиной L(H) имеют возможность экспоненциального роста в новой популяции.
Слайд 33
Влияние мутации: сохранение схем
Оператор мутации (ОМ) - это
случайное изменение гена в хромосоме с вероятностью РОМ.
Один
ген выживает с вероятностью (1-РОМ), то данная схема выживает, когда каждая из L(H) фиксированных позиций схемы выживает. Т.е. вероятность выживания при ОМ равна: .
Для малых величин РОМ << 1 это выражение может быть аппроксимировано
PS(OM) = 1 – О(H)·РОМ.
Слайд 34
Влияние кроссинговера и мутации: сохранение схем
Поскольку вероятность выживания
равна (1- вероятности разрушения при ОК и ОМ), то
схема H дает ожидаемое число особей в следующей популяции после выполнения всех генетических операторов ОР, ОК и ОМ согласно следующей формуле:
Слайд 35
Мутация
После выполнения оператора скрещивания полученные потомки с вероятностью
Рm подвергаются мутации, которая может быть выполнена различными способами.
Двоичная
мутация:1) Классическая мутация
2) Оператор инверсии
Мутация над вещественными числами:
1) Однородная мутация
2) Неоднородная мутация
Слайд 36
Мутация
Двоичная мутация:
1) Классическая мутация: замена случайно выбранного узла.
2)
Оператор инверсии: изменение прямого порядка следования генов в случайно
выбранном фрагменте хромосомы - на обратный.
Слайд 37
Сокращение промежуточной популяции
Глобальная редукция - промежуточную популяцию (репродукционную
группу) составляют все особи t-поколения, особи полученные в результате
скрещивания и мутации:1) Чистая замена
2) Элитарная схема.
3) Равномерная случайная замена.
4) Пропорциональная редукция.
5) Селекционная схема.
Локальная замена - особи выбираются из ограниченного окружения множества соседей. Замена особей потомками выполняется по такой же схеме. Таким образом сохраняется локальность информации.
Слайд 38
Чистая замена и Элитарная схема
В простейшем случае
с помощью скрещивания и мутации генерируются столько потомков, сколько
было родителей. Далее родители устраняются, а потомки формируют следующее поколение P(t+1).При этом каждая особь живет одно поколение. Такая схема часто используется в простом ГА. Однако при этом очевидно возможно, что некоторые очень хорошие решения могут быть заменены худшими, и лучшее решение будет потеряно.
В элитарной схеме потомков генерируется меньше, чем было родителей. Далее вновь построенные потомки заменяют худших родителей согласно значениям ЦФ. Для этой схемы возможна преждевременная сходимость к локальным экстремумам.
Слайд 39
Равномерная случайная замена и пропорциональная редукция
При равномерной случайной
замене потомков также генерируется меньше, чем было родителей, далее
случайно удаляется необходимое число родителей, которые заменяются новыми потомками.В методе пропорциональной редукции потомков генерируется больше, чем необходимо для замены. Потом заменяют заданное число родителей только лучшими потомками согласно значениям ЦФ.
Слайд 40
Селекционная схема
Родители и потомки выступают на равных правах,
все они помещаются в одну репродукционную группу. В ней
все особи этой группы ранжируются и в следующее поколение включаются только лучшие особей.Иногда применяется следующая модификация этого метода. Сначала вычисляется среднее значение ЦФ группы и в следующее поколение включаются те особи, у которых значение ЦФ больше среднего значения группы.
Слайд 41
Локальная замена
Родитель особи определяются первым родителем из локального
окружения (множества соседей). Для выбора удаляемых родителей и отбора
потомков для замены применяются следующие схемы:• Ввести в новое поколение каждого потомка и заменить случайным образом особи из их окружения;
• Ввести каждого потомка и заменить худшей особью соответственного окружения;
• Ввести потомка лучше, чем худшая особь в окружении и заменить худшие особи.
Слайд 42
ГА с изменяемой мощностью популяции
Если мощность популяции относительно
мала, то ГА работает быстро, но при этом увеличивается
опасность преждевременной сходимости к локальному экстремуму. С другой стороны большая мощность популяции увеличивает разнообразие генофонда, но процесс сходимости при этом замедляется, и требуются большие вычислительные ресурсыНа разных этапах работы ГА оптимальное значение мощности популяции может быть различным. Как вы думаете, на каких этапах популяция может быть сокращена, а на каких может быть расширена?
Слайд 43
Структура ГА с изменяемой мощностью популяции
Инициализация начальной популяции
p(t); Оценка ЦФ p(t);
Определение срока жизни особей популяции;
Повторяем следующее,
пока условие окончания не выполнено:t=t+1;
Увеличение возраста каждой особи на 1;
Рекомбинация p(t);
Мутация p(t);
Оценка ЦФ p(t);
Определение срока жизни новых особей;
Удаление из p(t) всех особей с возрастом больше срока жизни;
Слайд 44
ГА с изменяемой мощностью популяции
Срок жизни для каждой
особи определяется после оценки значений ЦФ и является окончательным
для данной особи (т.е. не изменяется в процессе эволюции). Особь живет определенное число поколений, а затем умирает по достижению срока жизни. Таким образом, срок жизни определяет число поколений, в течение которого особь живет (присутствует) в популяции.
Слайд 45
Стратегии определения срока жизни особи
1) Пропорциональный метод определения
срока жизни.
2) Линейный метод определения срока жизни.
3) Билинейный метод
определения срока жизни.
Слайд 46
Пропорциональный метод определения срока жизни
Срок жизни определяется формулой:
где
,
переменные L - означают минимальный и максимальный срок жизни, а f - значение ЦФ.
Соответствует в определенном смысле пропорциональному отбору родителей (метод «рулетки»).
Слайд 47
Линейный способ определения срока жизни особи
Срок жизни определяется
формулой:
где переменные L - означают минимальный и максимальный срок
жизни, а f - значение ЦФ.
Если в популяции много особей имеют значение ЦФ близкие к максимальному - такой подход приведет к чрезмерному увеличению размера популяции
Слайд 48
Билинейный способ определения срока жизни особи
Срок жизни определяется
формулой:
где переменные L - означают минимальный и максимальный срок
жизни, а f - значение ЦФ.
Слайд 49
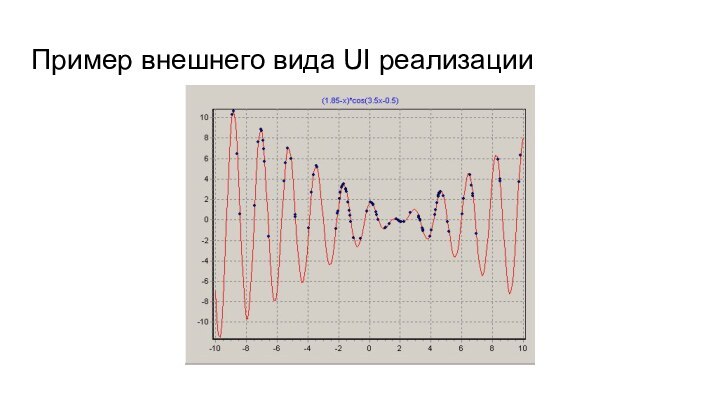
Пример решения задачи
Рассмотрим следующий пример, в котором для
функции
f(x)=(1,85 -x)*cos(3,5x – 0,5)
необходимо найти вещественное
, которое максимизирует f.В первую очередь необходимо определить характеристики пространства поиска и задать представление особи популяции ГА.
Какова мощность пространства поиска?
Слайд 50
Порядок решения задачи
Создание исходной популяции: приемлемые варианты.
Аргументация выбора
сбособа создания исходной популяции.
Кодирование особи-решения.
Выбор операторов кроссинговера и мутации.
Принятиее
решения о методе выбора родительских особей.Выбор подхода к сокращению популяции.
Реализация модели и графического симулятора.
Проверка работоспособности выбранной модификации модели ГА.
Определение оптимальных параметров ГА.
Оценка работы модели ГА и реализации.