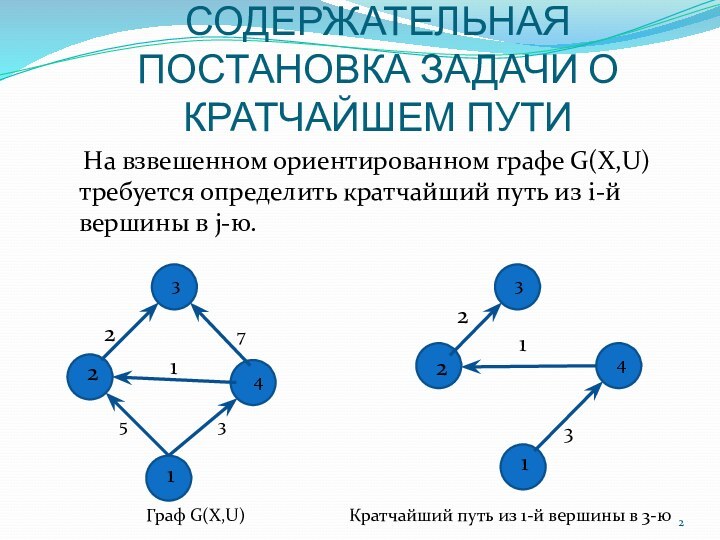
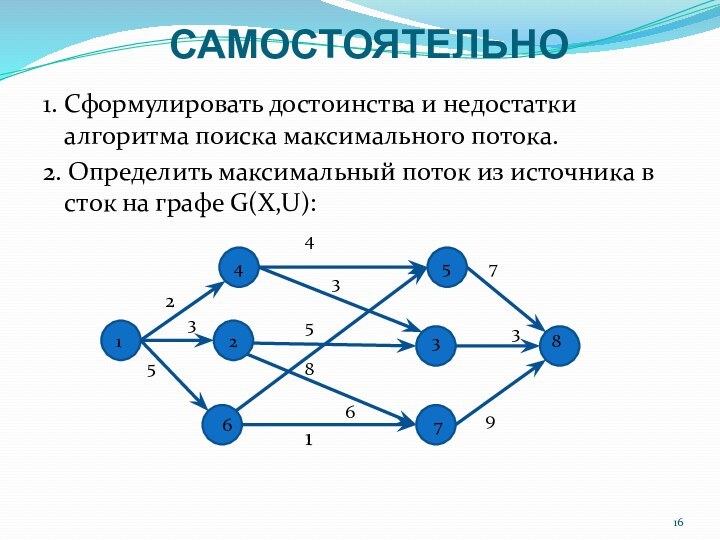
взвешенном ориентированном графе G(X,U) требуется определить кратчайший путь из
i-й вершины в j-ю. 1
2
3
4
1
2
3
4
2 7
5 3
1
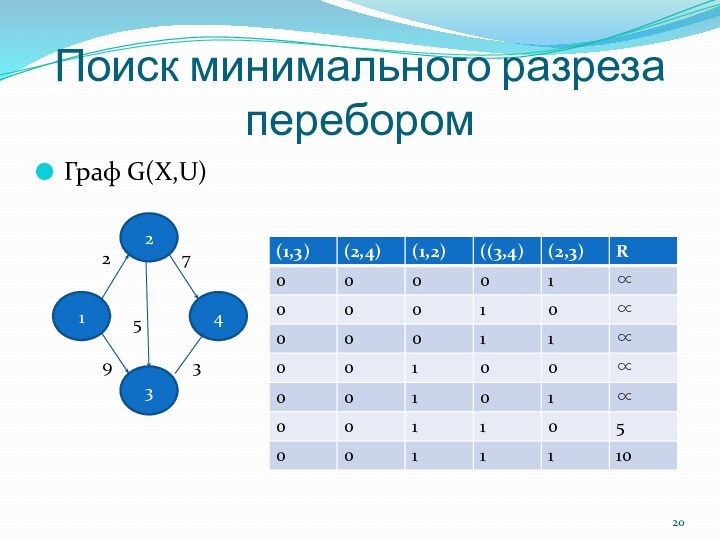
Граф G(X,U) Кратчайший путь из 1-й вершины в 3-ю
1
2
3