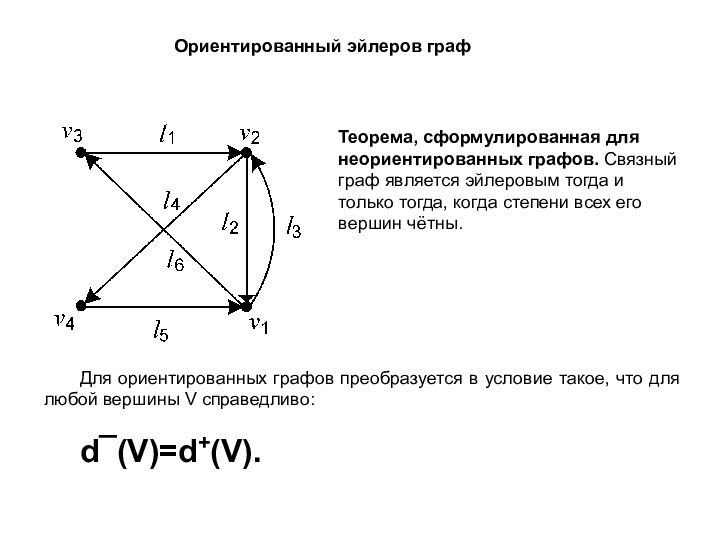
граф является эйлеровым тогда и только тогда, когда степени
всех его вершин чётны.Для ориентированных графов преобразуется в условие такое, что для любой вершины V справедливо:
d¯(V)=d+(V).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


![Лекция 6. Сетевые методы и графы в автоматизированном управлении Матрица достижимостей R=[rij] Все диагональные элементы в матрице R равны 1, поскольку](/img/tmb/15/1433352/37e21553524cf246b2e12f664837852a-720x.jpg)

![Лекция 6. Сетевые методы и графы в автоматизированном управлении Матрица инциденций B=[bij] Если граф G ориентированныйЕсли граф G неориентированныйРассмотрим граф G](/img/tmb/15/1433352/41d98cf7e9d8a8edcbb833c6debd2e8b-720x.jpg)
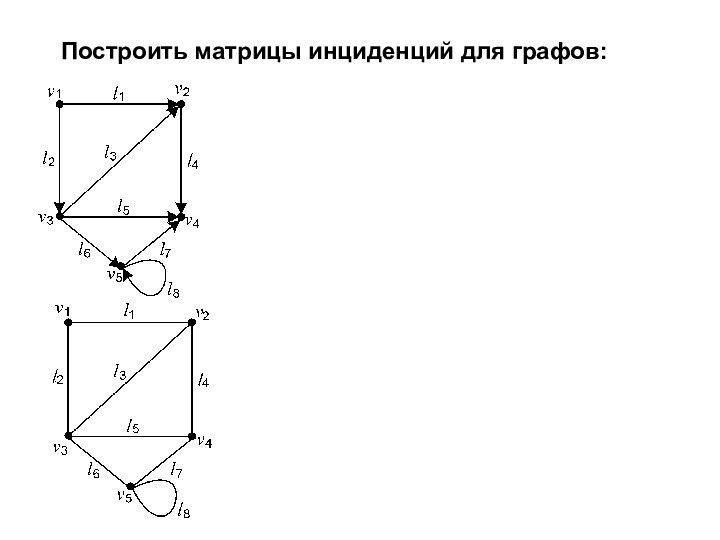

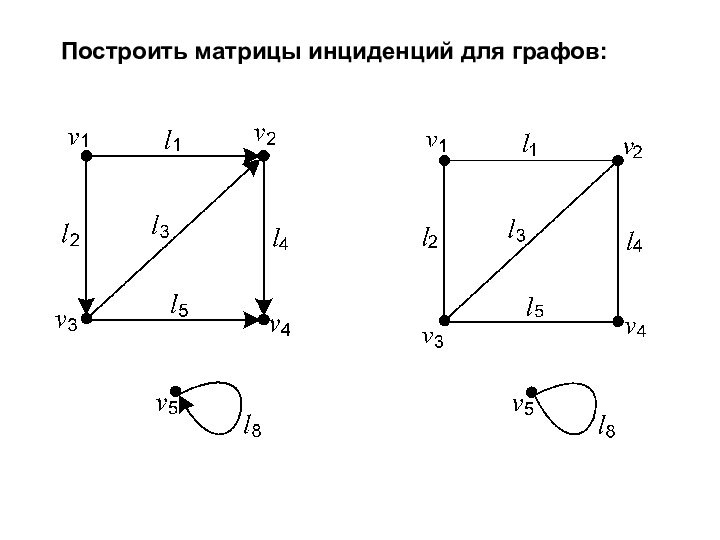
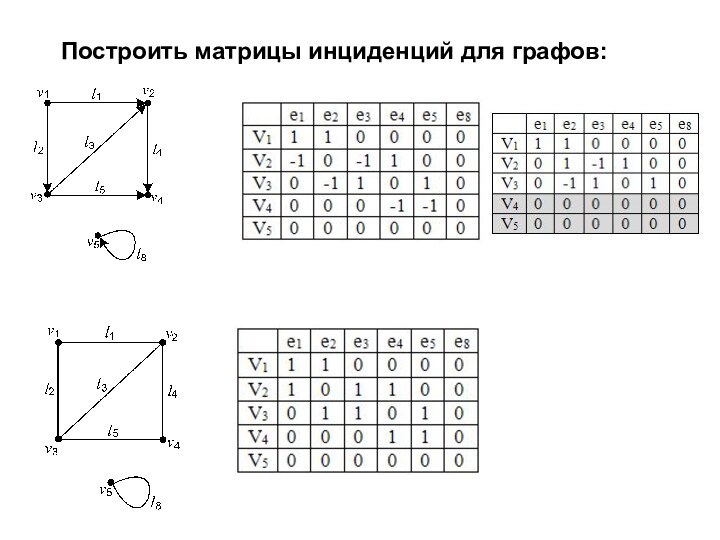
Для ориентированных графов преобразуется в условие такое, что для любой вершины V справедливо:
d¯(V)=d+(V).
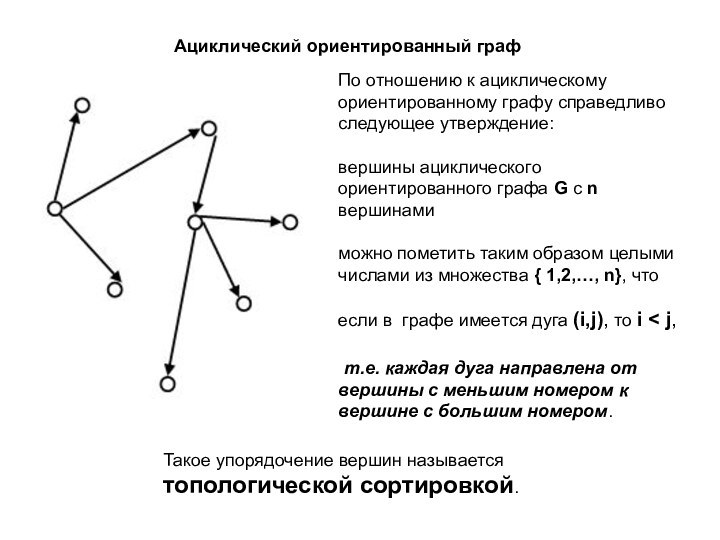
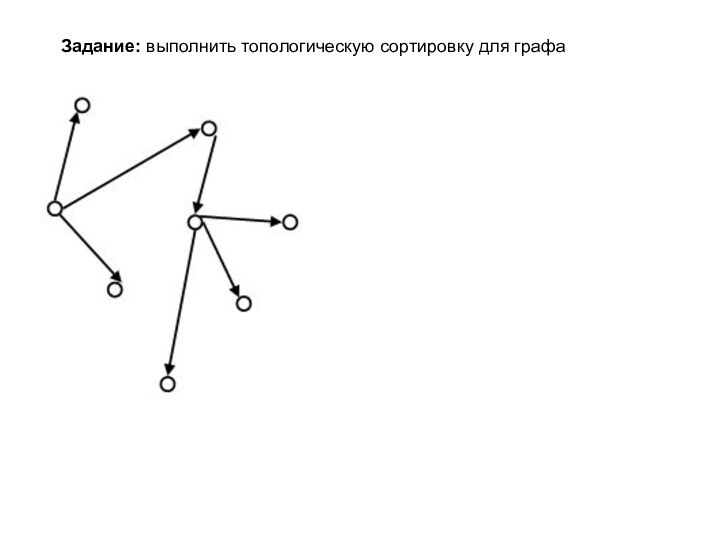
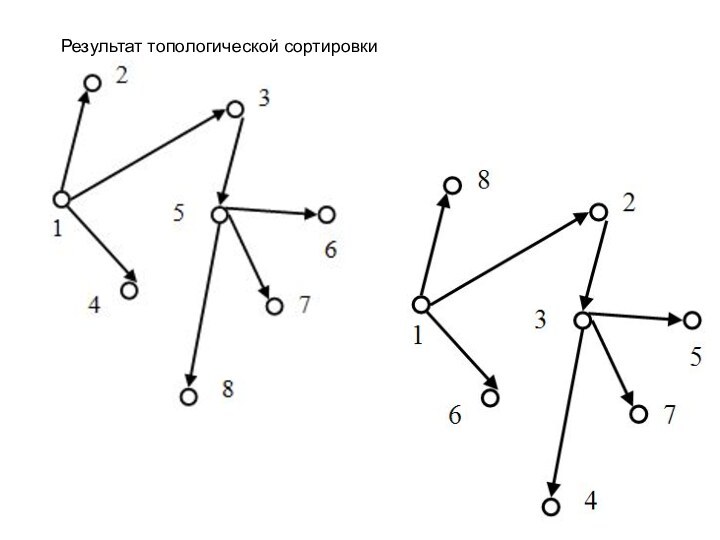
Такое упорядочение вершин называется
топологической сортировкой.
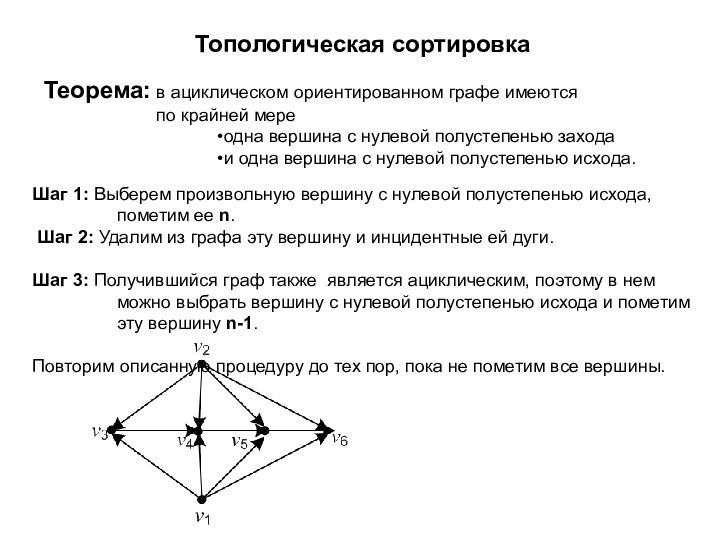
Шаг 1: Выберем произвольную вершину с нулевой полустепенью исхода, пометим ее n.
Шаг 2: Удалим из графа эту вершину и инцидентные ей дуги.
Шаг 3: Получившийся граф также является ациклическим, поэтому в нем можно выбрать вершину с нулевой полустепенью исхода и пометим эту вершину n-1.
Повторим описанную процедуру до тех пор, пока не пометим все вершины.
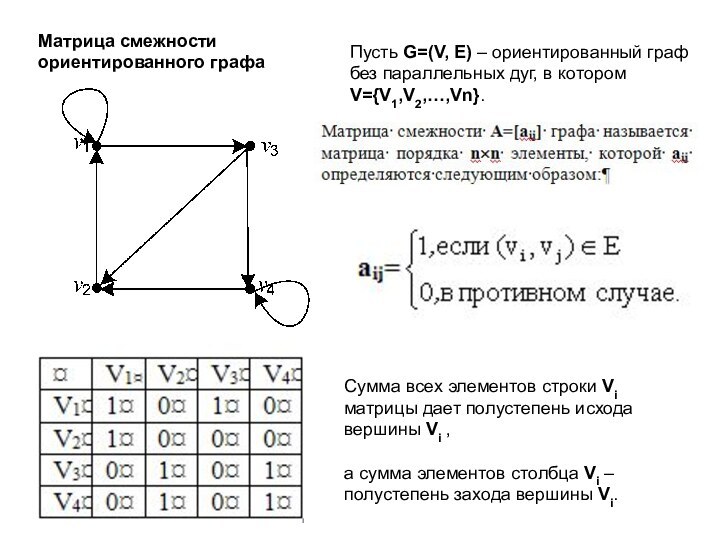
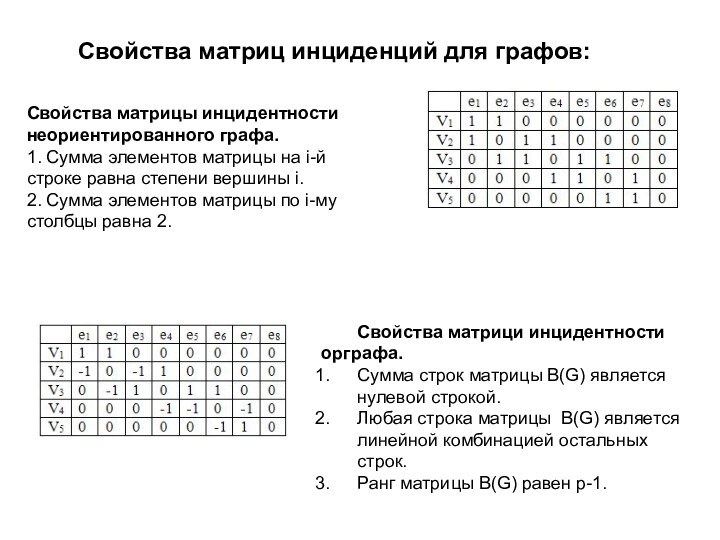
Сумма всех элементов строки Vi матрицы равна сумме элементов столбца Vi и равна степени вершины Vi.
Свойства матрици инцидентности орграфа.
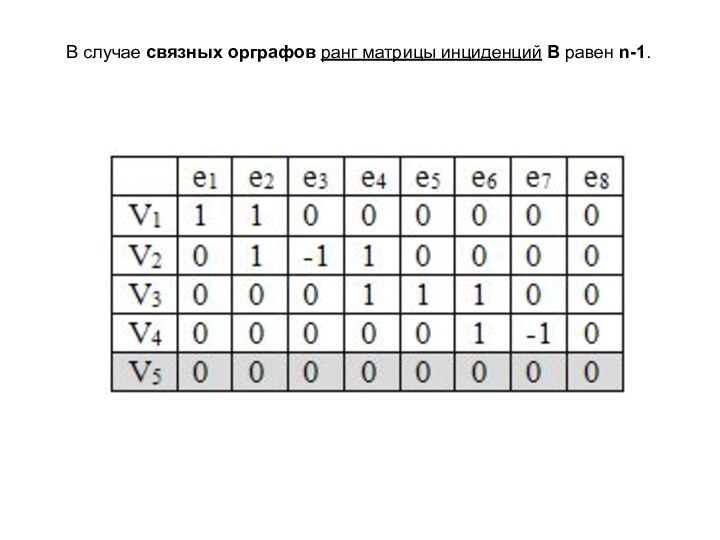
Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.