Слайд 2
Логика
Логика – это наука о формах
и способах
мышления
Законы логики отражают в сознании человека свойства, связи и
отношения объектов окружающего мира
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны
Слайд 3
Понятие
Понятие – это форма мышления, фиксирующая основные, существенные
признаки предмета
Компьютер
Множество электронных устройств
Множество электронных устройств
Слайд 4
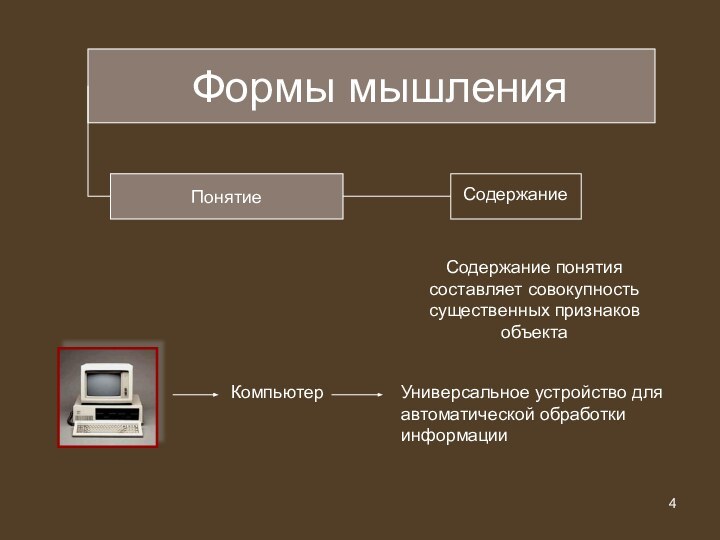
Формы мышления
Понятие
Содержание понятия составляет совокупность существенных признаков объекта
Компьютер
Универсальное
устройство для автоматической обработки информации
Слайд 5
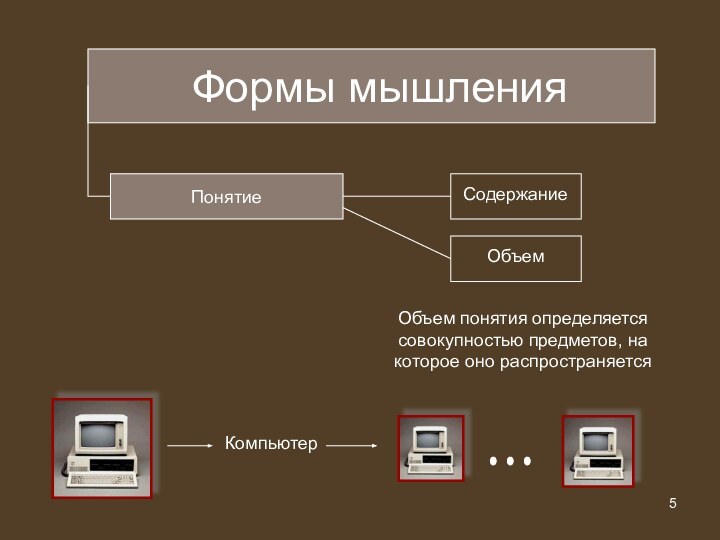
Формы мышления
Понятие
Объем понятия определяется совокупностью предметов, на которое
оно распространяется
Компьютер
Слайд 6
Формы мышления
Понятие
Высказывание
2 х 2 =4
- математический язык
Дважды два равно пять – естественный язык
- Истинно
- Ложно
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними. Высказывание может быть либо истинным, либо ложным
Алгебра высказываний определяет истинность или ложность
составных высказываний
Слайд 7
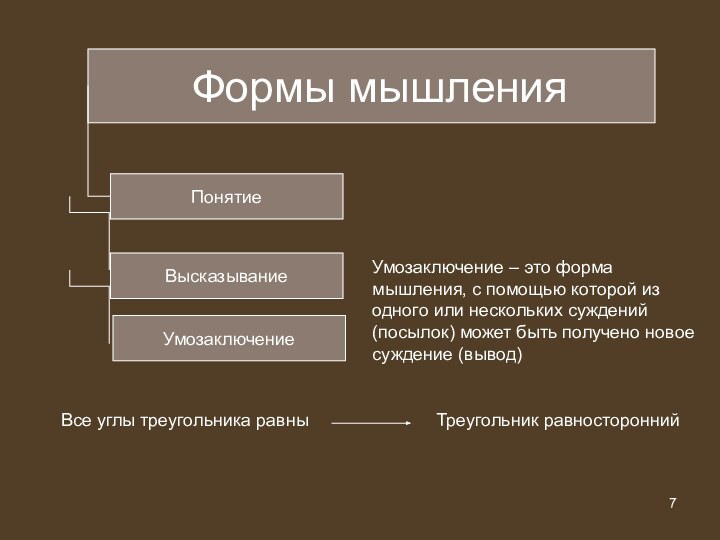
Формы мышления
Понятие
Высказывание
Все углы треугольника равны
Треугольник равносторонний
Умозаключение – это
форма мышления, с помощью которой из одного или нескольких
суждений (посылок) может быть получено новое суждение (вывод)
Умозаключение
Слайд 8
Алгебра высказываний
Алгебра высказываний служит для определения истинности или
ложности составных высказываний, не вникая в их содержание
Высказывания обозначаются
именами логических переменных
Логические переменные могут принимать значение:
1 – истина
0 – ложь
Слайд 9
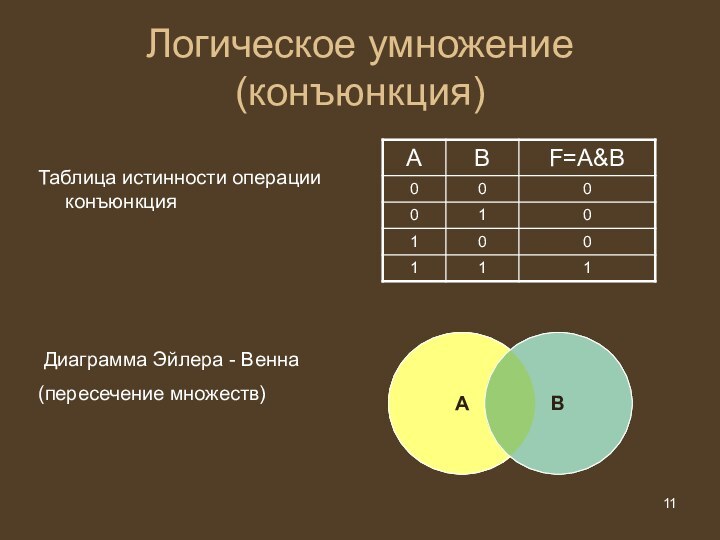
Логическое умножение (конъюнкция)
Объединение двух или более высказываний в
одно при помощи союза «И» называется операцией логического умножения
или конъюнкцией
Логическая конъюнкция выражается знаками &, ^, *
Составное высказывание, образованное в результате операции конъюнкции истинно только тогда, когда истинны входящие в него простые высказывания
Слайд 10
Логическое умножение (конъюнкция)
Пример
На улице идет дождь
На улице светит
солнце
Стоит теплая погода
Стоит холодная погода
На улице идет
дождь и стоит холодная погода Е = A & D
На улице светит солнце и стоит теплая погода F = B & C
На улице идет дождь и стоит теплая погода G = A & C
На улице светит солнце и стоит холодная погода H = B & D
Слайд 11
Логическое умножение (конъюнкция)
Таблица истинности операции конъюнкция
Диаграмма Эйлера -
Венна
А
В
(пересечение множеств)
Слайд 12
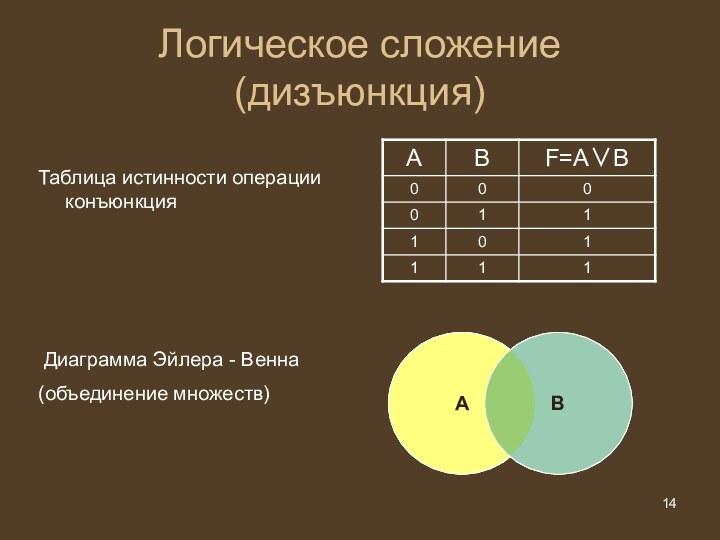
Логическое сложение (дизъюнкция)
Объединение двух или более высказываний в
одно при помощи союза «ИЛИ» называется операцией логического сложения
или дизъюнкцией
Логическая дизъюнкция выражается знаками ∨, +
Составное высказывание, образованное в результате операции дизъюнкции истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний
Слайд 13
Логическое сложение (дизъюнкция)
Пример
2 х 2 = 4
3 х
3 = 9
2 х 2 = 5
4 х
4 = 4
3 х 3 = 6
2 х 2 = 4 или 4 х 4 = 4 F = A ∨ D
3 х 3 = 9 или 2 х 2 = 5 G = B ∨ C
2 х 2 = 4 или 2 х 2 = 5 H = A ∨ C
2 х 2 = 5 или 3 х 3 = 6 I = С ∨ Е
Слайд 14
Логическое сложение (дизъюнкция)
Таблица истинности операции конъюнкция
Диаграмма Эйлера -
Венна
А
В
(объединение множеств)
Слайд 15
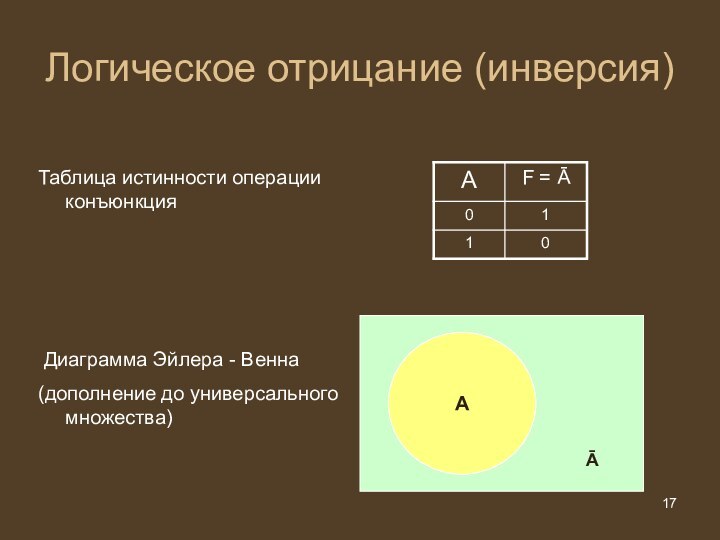
Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется
операцией логического отрицания или инверсией
Логическая дизъюнкция выражается знаками ‾,
т. е. : Ā
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное - истинным
Слайд 16
Логическое отрицание (инверсия)
Пример
2 х 2 = 5
- ложь
Ā. 2 х 2 = 5
- истинно
2 х 2 = 4 - истинно
Ā. 2 х 2 = 4 - ложь
2 х 2 = 4 - истинно
Слайд 17
Логическое отрицание (инверсия)
Таблица истинности операции конъюнкция
Диаграмма Эйлера -
Венна
А
(дополнение до универсального множества)
Ā
Слайд 18
Логические выражения и таблицы истинности
Логическое выражение
– это составное высказывание, которое можно выразить в виде
формулы, в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Пример
А = «2х2=5» - ложно (0)
В = «2х2=4» - истинно (1)
F = A или В и не А или не В
Слайд 19
Логические выражения и таблицы истинности
Для каждого
составного высказывания можно построить таблицу истинности, которая определяет истинность
или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных)
Количество строк в таблице истинности зависит от количества логических переменных (N):
Количество строк = 2 N
Слайд 20
Логические выражения и таблицы истинности
Логические выражения,
у которых таблицы истинности совпадают, называются равносильными
Задание
1
Составить таблицу истинности выражения ¯А& ¯В
Составить таблицу истинности выражения ¯(А∨В)
Задание 2
Составить таблицу истинности выражения ¯А ∨ ¯В
Составить таблицу истинности выражения ¯(А & В)
Слайд 21
Логические функции
Любое составное высказывание можно
рассматривать как логическую функцию F(X1, X2, …, XN), аргументами
которой являются логические переменные X1, X2, …, XN простые высказывания.
Функция и аргументы могут принимать только два различных значения «истинно» (1) и «ложь» (0).
Слайд 22
Логические функции
Рассмотрим произвольную
логическую функцию двух аргументов. Для построения таблицы истинности логической
функции:
Определяем количество строк в таблице истинности:
N1=22
N1 = 4, т. е. в таблице истинности 4 строки.
Определяем количество столбцов в таблице истинности:
N2=2N1,
N2=24,
N2 = 16, т. е. в таблице истинности 16 столбцов.
Вывод: существует 16 различных логических функций двух аргументов, каждая из которых задается своей таблицей истинности.
Слайд 23
Логические функции
Таблица истинности
логических функций двух аргументов
F2 – функция логического умножения
F8 –
функция логического сложения
F11 – функция логического отрицания для В
F13 – функция логического отрицания для А
Слайд 24
Логические функции
Логическое следование
Логическое следование (импликация) образуется соединением двух
высказываний в одно с помощью оборота «если …, то …».
Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание)
Логическая операция импликации («если А, то В») обозначается при помощи →, т. е. А → В
Слайд 25
Логические функции
Логическое следование
Таблица
истинности логической операции импликации («если А, то В») выражается
при помощи функции F14 А → В
Особенность: из ложной предпосылки может следовать что угодно.
Задание: Доказать равносильность высказываний
А → В и ¯А ∨ В
Слайд 26
Логические функции
Логическое равенство
Логическое равенство (эквивалентность) образуется соединением двух
высказываний в одно с помощью оборота «…тогда и только тогда, когда …».
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Логическая операция эквивалентности обозначается при помощи ~, т. е. А ~ В
Слайд 27
Логические функции
Логическое равенство
Таблица
истинности логической операции эквивалентности выражается при помощи функции F10
А ~ В
Задание: Какое из данных высказываний равносильно высказыванию А ~ В: 1) (¯А & ¯ В) ∨ ¯ (A & B)
2) (A ∨ ¯ В) & (¯А ∨ В)
Слайд 28
Логические законы и правила преобразования
Закон тождества
Всякое высказывание тождественно самому себе
А = А
Закон
непротиворечия
Высказывание не может быть одновременно истинным и ложным. Если высказывание А – истинно, то его отрицание ¯А - ложно. Значит, логическое произведение высказывания и его отрицания ложно:
А & ¯А = 0
Слайд 29
Логические законы и правила преобразования
Закон исключенного третьего
Высказывание не может быть одновременно истинным
и ложным. Если высказывание А – истинно, то его отрицание ¯А - ложно. Значит, логическое сложение высказывания и его отрицания истинно:
А ∨ ¯А = 1
Закон двойного отрицания
Если дважды отрицать двойное высказывание, в результате получим само высказывание:
¯ ¯ А = А
Слайд 30
Логические законы и правила преобразования
Законы Моргана: ¯(А∨В) = ¯А&
¯В
¯(А & В) = ¯А
∨ ¯В
Правило коммутативности: А ∨ В = В ∨ А
А & В = В & А
Правило ассоциативности: (А ∨ В) ∨ С = А ∨ (В ∨ С)
(А & В) & С = А & (В & С)
Правило дистрибутивности:a * b + a * c = a * ( b + c)
(А & В) ∨ ( A & С) = А & (В ∨ С)
(А ∨ В) & ( A ∨ С) = А ∨ (В & С)
Слайд 31
Логические законы и правила преобразования
Закон идемпотентности: А ∨ А
= А
А & А = А
Законы исключения
констант: А ∨ 1 = 1
А ∨ 0 = А
А & 0 = 0
А & 1 = А
Закон контрапозиции (правило перевертывания): А ~ В = В ~ А
Закон поглощения: А ∨ ( А & В) = А
А & ( А ∨ В) = А
Закон исключения (склеивания): (А ∨ В) & (¯ А ∨ В) = В
(А & В) ∨ (¯ А & В) = В
Слайд 32
Задания
Упростить логические выражения:
(А & В) ∨ ( А
& ¯ B)
(А ∨ ¯ A) & B
A &
( A ∨ B) & ( C ∨ ¯ B)
A & ¯ B ∨ B & C ∨ ¯ A & ¯ B
A ∨ ¯ A & B
Слайд 33
Решение логических задач
Для решения логических задач их необходимо
формализовать, т. е. записать на языке алгебры высказываний. Полученные
логические выражения необходимо упростить и проанализировать, для чего – построить таблицу истинности высказывания.
Пример
В каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики.
На аудиториях повесили таблички.
На первой – «По крайней мере, в одной из этих аудиторий размещается кабинет информатики».
На второй – «Кабинет физики находится в другой аудитории».
Известно, что надписи на табличках либо обе истинны, либо обе ложны.
Где находится кабинет информатики?
Слайд 34
Решение логических задач
Пусть
А – «В первой аудитории находится
кабинет информатики»
В – «Во второй аудитории находится кабинет информатики»
Тогда
¯
А – «В первой аудитории находится кабинет физики»
¯ В – «Во второй аудитории находится кабинет физики»
Высказывание, содержащееся на табличке на первой аудитории:
Х = А ∨ В
Высказывание, содержащееся на табличке на второй аудитории:
Y = ¯ А
Слайд 35
Решение логических задач
Утверждение, что надписи на табличках либо
одновременно истинны, либо ложны, в соответствии с законом исключающего
третьего:
(X & Y) ∨ ( ¯ X & ¯ Y ) = 1
Подставим вместо X и Y соответствующие значения. Тогда,
(X & Y) ∨ ( ¯ X & ¯ Y ) = (( А ∨ В) & ¯ А ) ∨ ¯ ( А ∨ В) & ¯ ¯ A =
= ( А & ¯ А ∨ В & ¯ А ) ∨ ( ¯ А & ¯ В & А) =
= ( 0 ∨ В & ¯ А ) ∨ ( 0 & ¯ В ) = ( 0 ∨ В & ¯ А ) ∨ 0 = В & ¯ А
Слайд 36
Решение логических задач
Строим таблицу истинности высказывания В &
¯ А :
Следовательно:
Во второй аудитории – кабинет информатики,
В первой
аудитории – кабинет физики
Слайд 37
Решение логических задач
Задача
В процессе составления расписания уроков учителя
высказали свои пожелания, Учитель математики хочет иметь первый или
второй урок, учитель физики – второй или третий уроки. Сколько существует возможных вариантов расписания и какие они?
Слайд 38
Логические основы устройства компьютера
Т. к. любая логическая функция
может быть представлена в виде трех основных элементарных логических
операций, любые устройства компьютера могут быть собраны из базовых логических элементов, как из кирпичиков.
Логический элемент «И» - логическое умножение
Логический элемент «ИЛИ» - логическое сложение
Логический элемент «НЕ» - инверсия
Дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.
Слайд 39
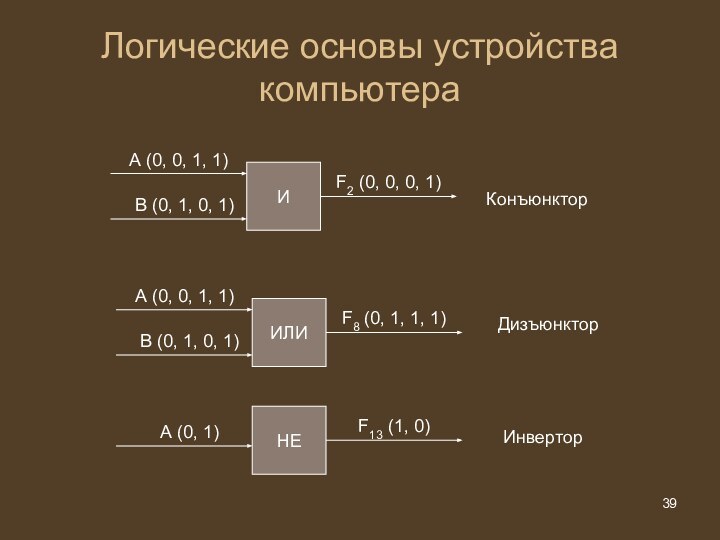
Логические основы устройства компьютера
И
А (0, 0, 1, 1)
В
(0, 1, 0, 1)
F2 (0, 0, 0, 1)
ИЛИ
А (0,
0, 1, 1)
В (0, 1, 0, 1)
F8 (0, 1, 1, 1)
НЕ
А (0, 1)
F13 (1, 0)
Конъюнктор
Дизъюнктор
Инвертор
Слайд 40
Логические основы устройства компьютера
Все многообразие математических операций
в процессоре сводится к сложению двоичных чисел.
Сложение двоичных
чисел обеспечивает сумматор.
Слайд 41
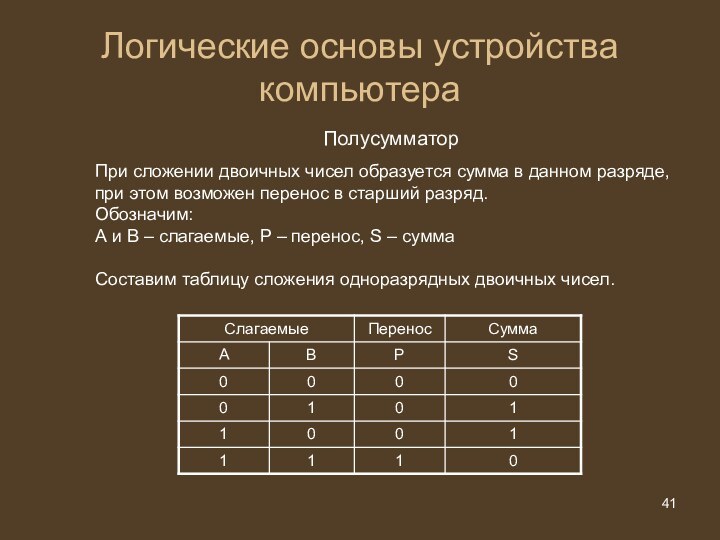
Логические основы устройства компьютера
Полусумматор
При сложении двоичных чисел
образуется сумма в данном разряде, при этом возможен перенос
в старший разряд.
Обозначим:
А и В – слагаемые, Р – перенос, S – сумма
Составим таблицу сложения одноразрядных двоичных чисел.
Слайд 42
Логические основы устройства компьютера
Перенос Р можно реализовать с
помощью операции логического умножения:
Р = А & B
Составим формулу
для вычисления суммы.
S = ( А ∨ В ) & ¯ ( А & B )
Задание
Построить таблицу истинности для данного высказывания.
Слайд 43
Логические основы устройства компьютера
Построим из базовых логических элементов
схему полусумматора.
Р = А & B
Для реализации переноса используем
логический элемент «И».
И
А (0, 0, 1, 1)
В (0, 1, 0, 1)
P (0, 0, 0, 1)
Устройства компьютера (сумматоры в процессоры, ячейки памяти в оперативной памяти) строятся на основе базовых логических элементов.
Слайд 44
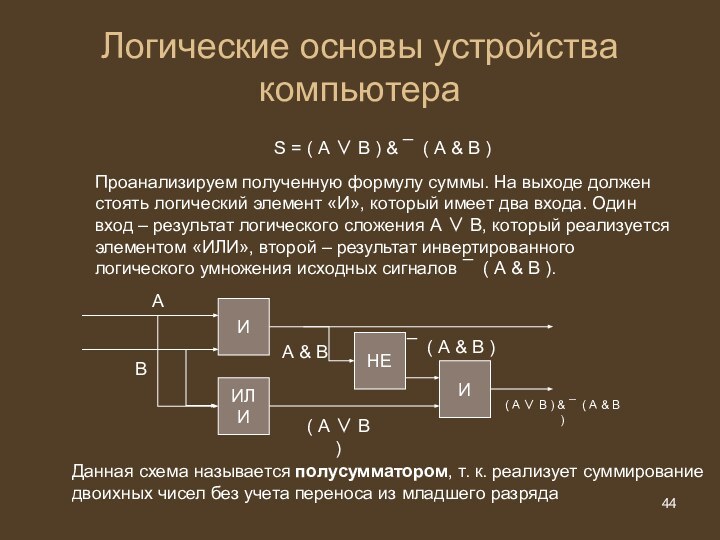
Логические основы устройства компьютера
S = ( А ∨
В ) & ¯ ( А & B )
Проанализируем
полученную формулу суммы. На выходе должен стоять логический элемент «И», который имеет два входа. Один вход – результат логического сложения А ∨ В, который реализуется элементом «ИЛИ», второй – результат инвертированного логического умножения исходных сигналов ¯ ( А & B ).
И
А
В
ИЛИ
НЕ
И
А & B
¯ ( А & B )
( А ∨ В )
( А ∨ В ) & ¯ ( А & B )
Данная схема называется полусумматором, т. к. реализует суммирование двоихных чисел без учета переноса из младшего разряда
Слайд 45
Логические основы устройства компьютера
Одноразрядный сумматор
Полный одноразрядный сумматор должен
иметь
три входа: А, В – слагаемые, Р0 –
перенос из младшего разряда
два выхода: сумма S и перенос P
Задание
Построить таблицу истинности для реализации сложения.
Слайд 46
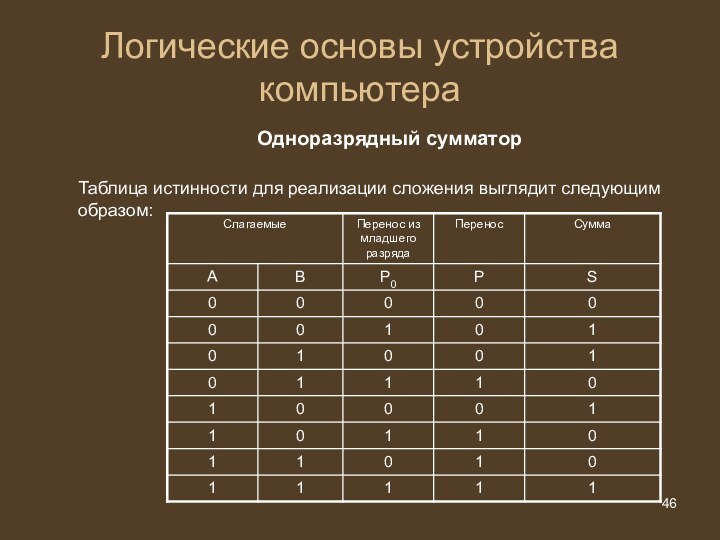
Логические основы устройства компьютера
Одноразрядный сумматор
Таблица истинности для реализации
сложения выглядит следующим образом:
Слайд 47
Логические основы устройства компьютера
Одноразрядный сумматор
P реализуется путем логического
сложения результатов попарного логического умножения входных данных:
Р = (
А & В ) ∨ ( А & Р0 ) ∨ ( В & Р0 )
S реализуется путем логического умножения инвертированного переноса ¯ Р на результат логического сложения входных данных:
S = ( А ∨ В ∨ Р0) & ¯ Р
S дает правильное значение во всех случаях, кроме случая, когда все входные переменные принимают значение 1. Сложим S с результатом логического умножения входных переменных:
S = ( А ∨ В ∨ Р0) & ¯ Р0 ∨ ( А & В & Р0)
Слайд 48
Логические основы устройства компьютера
Многоразрядный сумматор
Многоразрядный сумматор процессора состоит
из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный
сумматор, причем выход младшего разряда подключен к входу сумматора старшего разряда.
Слайд 49
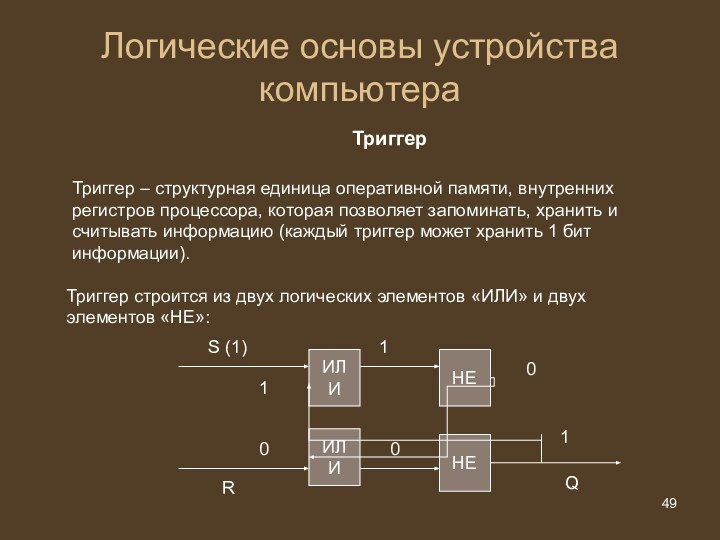
Логические основы устройства компьютера
Триггер
Триггер – структурная единица оперативной
памяти, внутренних регистров процессора, которая позволяет запоминать, хранить и
считывать информацию (каждый триггер может хранить 1 бит информации).
Триггер строится из двух логических элементов «ИЛИ» и двух элементов «НЕ»:
ИЛИ
ИЛИ
НЕ
НЕ
1
0
1
S (1)
R
0
0
1
Q
Слайд 50
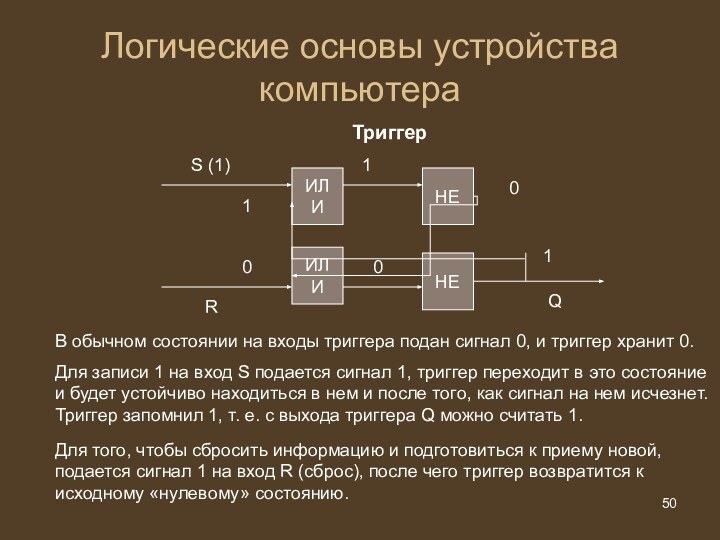
Логические основы устройства компьютера
Триггер
ИЛИ
ИЛИ
НЕ
НЕ
1
0
1
S (1)
R
0
0
1
Q
В обычном состоянии на
входы триггера подан сигнал 0, и триггер хранит 0.
Для
записи 1 на вход S подается сигнал 1, триггер переходит в это состояние и будет устойчиво находиться в нем и после того, как сигнал на нем исчезнет. Триггер запомнил 1, т. е. с выхода триггера Q можно считать 1.
Для того, чтобы сбросить информацию и подготовиться к приему новой, подается сигнал 1 на вход R (сброс), после чего триггер возвратится к исходному «нулевому» состоянию.
Слайд 51
Логические основы устройства компьютера
Вопросы
Какой сигнал будет на выходе
логического элемента «И», если на вход будут поданы сигналы
А=0, В=1?
Какой сигнал будет на выходе логического элемента «ИЛИ», если на вход будут поданы сигналы А=0, В=1?
Какой сигнал будет на выходе логического элемента «НЕ», если на вход будут поданы сигналы А=0; А=1?
Для чего необходим сумматор?
Чем отличается полный сумматор от полусумматора?
Как устроен полноразрядный сумматор?
Для чего необходим и где используется триггер?
Слайд 52
Логические основы устройства компьютера
Задания № 3
По заданной логической
функции F(A,B) = (B & ¯ A) ∨ (
¯ B & A) построить логическую схему.
Построить таблицу истинности, описывающую состояние входов и выходов RS - триггера
Какое количество базовых логических элементов необходимо для реализации 64-разрядного сумматора?
Какое количество базовых логических элементов образуют оперативную память современного ПК объемом 64 Мбайта?
Слайд 53
Логические основы устройства компьютера
Задания № 4
Упростить выражения:
¯ ( А & B ) ∨ ¯
( А & C ) ∨ ¯ ( B & C )
(A & ¯ ( B ∨ C )) ∨ (A ∨ ¯ ( B & C ))
¯ ( ¯ B & ¯ C ) ∨ ¯ ( ¯ A & ¯ C ) ∨ ¯ ( ¯ A & ¯ B )
(А ∨ ( А & В)) & ( А & ( А ∨ В))
( (А ∨ В) & (¯ А ∨ В) ) ∨ ( (А & В) ∨ (¯ А & В) )
¯ ( (А ∨ В) & (¯ А ∨ В) ) & ¯ ( ¯ A & ¯ B )
Слайд 54
Логические основы устройства компьютера
Задания № 5
Решить логические задачи:
1.
Джеку, Питеру и Майклу предъявлено обвинение в соучастии в
ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Джек показал, что преступники скрылись на синем Мерседесе, Питер сказал, что это был черный Джип, а Майкл утверждал, что это был Форд Мустанг и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо марку машины, либо только ее цвет. Какого цвета и какой марки была машина?
Слайд 55
Логические основы устройства компьютера
Задания № 5
Решить логические задачи:
2.
По телевизору синоптик объявляет прогноз погоды на завтра и
утверждает следующее:
Если не будет ветра, то будет пасмурная погода без дождя
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Какая будет погода?
Слайд 56
Логические основы устройства компьютера
Задания № 5
Построить логическую схему
по данному выражению и найти его значение при указанных
параметрах:
¯ ( А & B ) ∨ ¯ ( B & ¯ C ), при А=0, В=1, С=0
¯ ( ¯ B & ¯ C ) ∨ ¯ ( ¯ A & ¯ C ), при А=1, В=1, С=1
(А ∨ ( А & В)) & ( А & ( А ∨ В)), при А=1, В=1
( (А ∨ В) & (¯ А ∨ В) ) ∨ ( (А & В) ∨ (¯ А & В) ), при А=1, В=0, С=1
Слайд 57
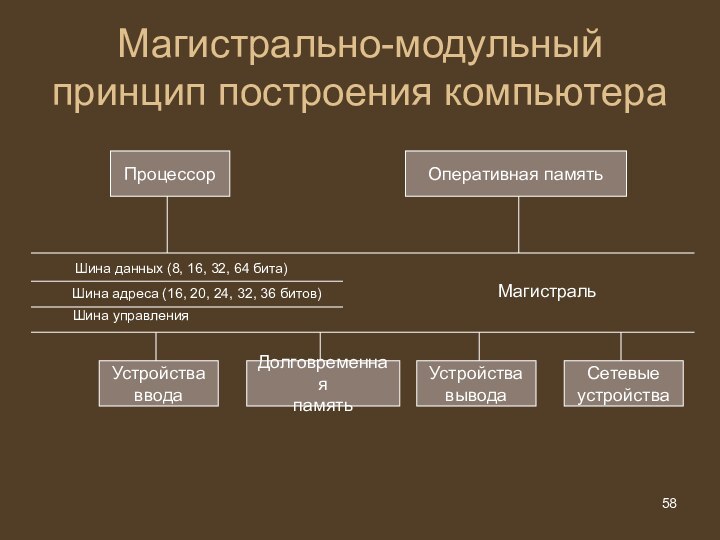
Магистрально-модульный принцип построения компьютера
В основу архитектуры современных ПК
положен магистрально-модульный принцип.
Модульный принцип позволяет потребителю самому комплектовать нужную
ему конфигурацию компьютера и производить при необходимости ее модернизацию
Модульная организация ПК опирается на магистральный (шинный) принцип обмена информацией между устройствами
Слайд 58
Магистрально-модульный принцип построения компьютера
Процессор
Оперативная память
Шина данных (8, 16,
32, 64 бита)
Шина адреса (16, 20, 24, 32, 36
битов)
Шина управления
Магистраль
Устройства
ввода
Долговременная
память
Устройства
вывода
Сетевые
устройства
Слайд 59
Магистраль
Магистраль (системная шина включает в себя три многоразрядные
шины:
шину данных,
шину адреса,
шину управления
Обмен информацией между устройствами
происходит на машинном языке последовательностями нулей и единиц в форме электрических импульсов
Слайд 60
Шина данных
По шине данных происходит передача данных от
устройства к устройству в любом направлении
Разрядность шины данных определяется
разрядностью процессора, т. Е. количеством двоичных разрядов, которые могут обрабатываться или передаваться процессором одновременно
Разрядность постоянно увеличивается по мере развития компьютерной техники.
Выбор устройства или ячейки памяти, куда пересылаются или откуда считываются данные по шине данных производит процессор
Слайд 61
Шина адреса
По шине адреса происходит передача адреса от
процессора к оперативной памяти и устройствам (однонаправленная шина)
Каждое устройство
или ячейка оперативной памяти имеет свой адрес
Выбор устройства или ячейки памяти, куда пересылаются или откуда считываются данные по шине данных производит процессор
Слайд 62
Шина адреса
Разрядность шины адреса определяет объем адресуемой памяти
(адресное пространство), которые могут иметь уникальные адреса. Количество таких
адресуемых ячеек памяти можно рассчитать по формуле:
N=2I
где I – разрядность шины адреса
В современных ПК I = 36, следовательно, максимально возможное количество адресуемых ячеек памяти равно:
N=236 = 68.719.476.736
Слайд 63
Шина управления
По шине управления передаются сигналы, определяющие характер
обмена информацией по магистрали
Сигналы управления показывают, какую операцию –
считывание или запись – информации из памяти нужно производить
Сигналы управления синхронизируют обмен информацией между устройствами
Слайд 64
Процессор
Процессор реализуется на большой интегральной схеме, изготовленной по
миллимикронной технологии внутри полупроводникового кристалла и содержащей десятки миллионов
электронных элементов, способных выполнять логические операции или хранить информацию
Слайд 65
Тактовая частота
2500 – 4000 МГц
Такт – промежуток времени
между началами подачи двух последовательных импульсов специальной микросхемой –
генератором тактовой частоты, синхронизующим работу узлов ПК.
На выполнение процессором каждой операции отводится определенное количество тактов. Чем больше частота, тем больше операций в секунду выполняет процессор.
Тактовая частота измеряется в мегагерцах (МГц) и гигагерцах (ГГц). 1 МГц = 1.000.000 тактов в секунду
Слайд 66
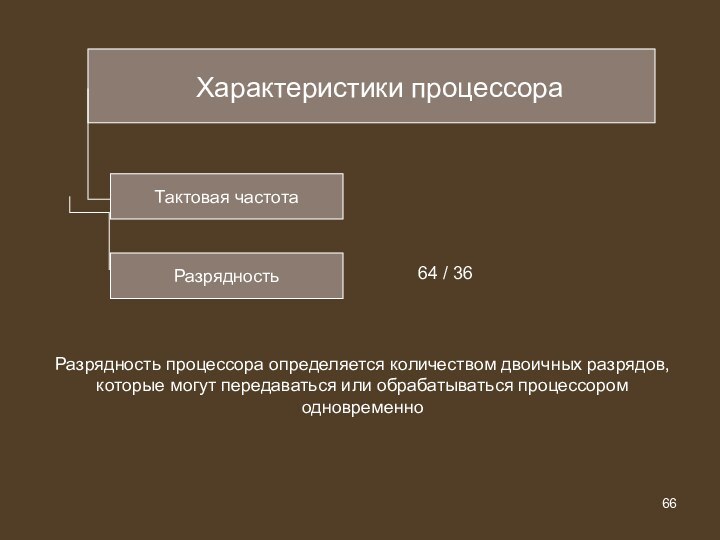
Разрядность
Разрядность процессора определяется количеством двоичных разрядов, которые могут
передаваться или обрабатываться процессором одновременно
Тактовая частота
64 / 36
Слайд 67
Разрядность
Производительность является интегральной характеристикой, которая зависит от частоты
процессора, его разрядности, а также особенности архитектуры. Производительность нельзя
вычислить
Тактовая частота
Производительность
Слайд 68
Оперативная память
Оперативная память предназначена для хранения информации и
изготавливается в виде модулей памяти.
Быстродействие модулей памяти зависит от
максимально возможной частоты операций записи или считывания информации из ячеек памяти.
Современные модули памяти обеспечивают частоту до 800 МГц, их информационная емкость до 512 Мбайт