- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Представление о системах счисления
Содержание
- 2. Совокупность приемов наименования и записи чисел называется
- 3. Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.
- 4. В зависимости от способов изображения чисел цифрами,
- 5. В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
- 6. Основные позиционные системы счисленияДвоичная система счисления используется
- 7. Основные позиционные системы счисления Шестнадцатеричная система счисления
- 8. Основные позиционные системы счисления Троичная система счисления Использует
- 9. Основные позиционные системы счисления Система счисления с
- 10. Основные позиционные системы счисления Система счисления с
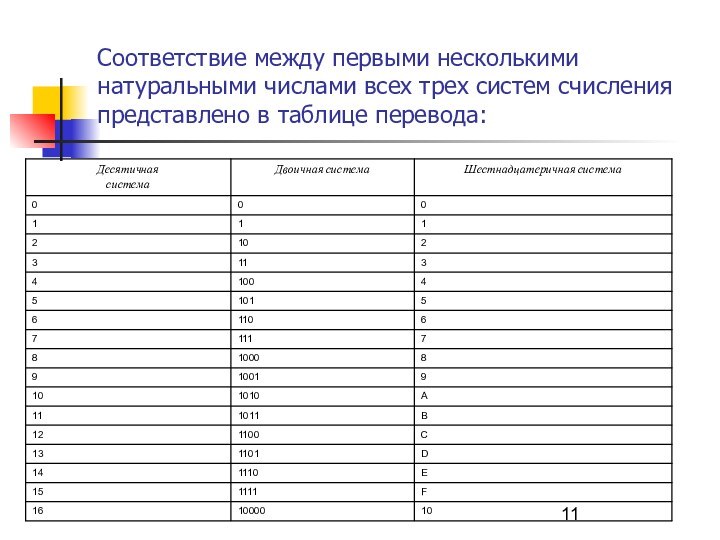
- 11. Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в таблице перевода:
- 12. Правила перевода целых чиселПеревод из десятичной системы
- 13. Пример 1. Выполнить перевод числа 19 в двоичную систему счисления:Таким образом, 19 = 100112.
- 14. Пример 2. Выполнить перевод числа 19 в
- 15. Пример 3. Выполнить перевод числа 123 в
- 16. Пример 4. Выполнить перевод числа 0,847
- 17. Перевод из двоичной и шестнадцатеричной систем счисления
- 18. Пример 5. Выполнить перевод числа 1316 в
- 19. Из двоичной системы счисления в шестнадцатеричную:
- 20. Пример 7. Выполнить перевод числа 100112 в
- 21. Перевод из шестнадцатеричной системы счисления в двоичную:
- 22. Пример 8. Выполнить перевод числа 1316 в
- 23. Правила выполнения простейших арифметических действийАрифметические операции для
- 24. Пример 1. Сложить двоичные числа 1101 и
- 25. Проверим результат. Для этого определим полные значения
- 26. Процесс образования суммы по разрядам описан ниже:
- 27. Правила умножения Таблица умножения двоичных цифр приведена ниже (обозначения строк и столбцов соответствуют слагаемым):
- 28. Пример 2. Перемножить двоичные числа 101 и
- 29. Процесс образования результата по шагам умножения множимого
- 30. Скачать презентацию
- 31. Похожие презентации



























Слайд 3 Количество знаков или символов, используемых для изображения числа,
называется основанием системы счисления.
Слайд 4 В зависимости от способов изображения чисел цифрами, системы
счисления делятся на непозиционные и позиционные.
Позиционной системой счисления
называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления).Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти).
Слайд 5 В современной информатике используются в основном три системы
счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
Слайд 6
Основные позиционные системы счисления
Двоичная система счисления используется для
кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое
положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1. Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.
Слайд 7
Основные позиционные системы счисления
Шестнадцатеричная система счисления используется для
кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь
– специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.
Слайд 8
Основные позиционные системы счисления
Троичная система счисления
Использует три цифры
– 0, 1 и 2, а также символы «+»
и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа.В более далекой перспективе просматривается возможность перехода компьютерной отрасли на троичную систему счисления, так как она позволяет более эффективно сворачивать числовую информацию (как показал Джон фон Нейман, это следует из того, что число 3 ближе, чем 2, к основанию натуральных логарифмов).
Слайд 9
Основные позиционные системы счисления
Система счисления с основанием 4.
Использует
четыре цифры – 0, 1, 2 и 3, а
также символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа. О практическом использовании этой системы счисления пока ничего не известно. Однако перспектива есть по двум причинам. Во-первых, аналогичная 8 и 16 связь с двоичной системой, что позволяет легко переводить числа из любой из этих систем в любую другую. Во-вторых, наличие именно 4 базовых аминокислот, ставших своеобразным алфавитом быстро развивающейся генетики.
Слайд 10
Основные позиционные системы счисления
Система счисления с основанием 7.
Семь
дней недели, семь нот, семь чудес Света, семь цветов
радуги (хотя нормальный глаз видит их там только шесть, не разделяя оттенков синего и голубого) и многочисленные другие примеры указывают на то, что и это число служило разрядной единицей.А название праздника «пятидесятница», как и пришедший из древнееврейского языка «юбилей» – это вовсе не половина от ста, а число, следующее за 49 – второй разрядной единицей системы счисления с основанием 7.
Слайд 11 Соответствие между первыми несколькими натуральными числами всех трех
систем счисления представлено в таблице перевода:
Слайд 12
Правила перевода целых чисел
Перевод из десятичной системы счисления
в двоичную и шестнадцатеричную:
а) исходное целое число делится
на основание системы счисления, в которую переводится (на 2 - при переводе в двоичную систему счисления или на 16 - при переводе в шестнадцатеричную); получается частное и остаток;б) если полученное частное меньше основания системы счисления, в которую выполняется перевод, процесс деления прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);
в) все полученные остатки и последнее частное преобразуются в соответствии с таблицей перевода в цифры той системы счисления, в которую выполняется перевод;
г) формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.
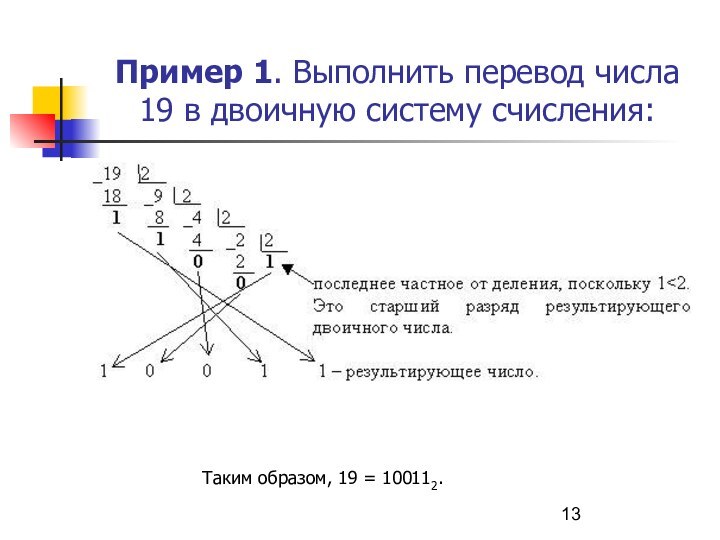
Слайд 13 Пример 1. Выполнить перевод числа 19 в двоичную
систему счисления:
Таким образом, 19 = 100112.
Слайд 14 Пример 2. Выполнить перевод числа 19 в шестнадцатеричную
систему счисления:
Таким образом, 19 = 1316.
Слайд 15 Пример 3. Выполнить перевод числа 123 в шестнадцатеричную
систему счисления:
Здесь остаток 11 преобразован в шестнадцатеричную цифру В
и после этого данная цифра вошла в число. Таким образом, 123 = 7В16.Слайд 16 Пример 4. Выполнить перевод числа 0,847 в двоичную
систему счисления. Перевод выполнить до четырех значащих цифр после
запятой. Имеем:
Таким образом, 0,847 = 0,11012.
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.
Слайд 17 Перевод из двоичной и шестнадцатеричной систем счисления в
десятичную. В этом случае рассчитывается полное значение числа по
формуле:где l – количество разрядов числа, уменьшенное на 1,
i – порядок разряда,
m – основание системы счисления,
ai – множитель, принимающий любые целочисленные значения от 0 до m-1, и соответствующий цифре i-го порядка числа.
Например, для десятичного (m = 10) числа 345 его полное значение рассчитывается по формуле:
3*102 + 4*101 + 5*100 = 345.
Слайд 18 Пример 5. Выполнить перевод числа 1316 в десятичную
систему счисления. Имеем: 1316 = 1*161 + 3*160 = 16
+ 3 = 19. Таким образом, 1316 = 19. Пример 6. Выполнить перевод числа 100112 в десятичную систему счисления. Имеем: 100112 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16+0+0+2+1 = 19. Таким образом, 100112 = 19.
Слайд 19
Из двоичной системы счисления в шестнадцатеричную:
Исходное число
разбивается на тетрады (т.е. 4 цифры), начиная с младших
разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4; каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицейСлайд 20 Пример 7. Выполнить перевод числа 100112 в шестнадцатеричную
систему счисления.
Поскольку в исходном двоичном числе количество цифр
не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:
В соответствии с таблицей 00112 = 112 = 316 и 00012 = 12 = 116. Тогда 100112 = 1316.
Слайд 21
Перевод из шестнадцатеричной системы счисления в двоичную:
а)
каждая цифра исходного числа заменяется тетрадой двоичных цифр в
соответствии с таблицей. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;б) незначащие нули в результирующем числе отбрасываются.
Слайд 22 Пример 8. Выполнить перевод числа 1316 в двоичную
систему счисления.
По таблице имеем:
116 = 12 и
после дополнения незначащими нулями двоичного числа 12 = 00012; 316 = 112 и после дополнения незначащими нулями двоичного числа 112 = 00112.
Тогда 1316 = 000100112.
После удаления незначащих нулей имеем 1316 = 100112.
Слайд 23
Правила выполнения простейших арифметических действий
Арифметические операции для двоичных
и шестнадцатеричных чисел выполняются по тем же правилам, что
и для десятичных чисел.Правила сложения
Таблица сложения двоичных цифр имеет вид
Слайд 24
Пример 1. Сложить двоичные числа 1101 и 11011.
Запишем
слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду
номер 1:Слайд 25 Проверим результат. Для этого определим полные значения слагаемых
и суммы
11012 = 1*23 +1*22 + 0*21 +
1*20 = 8 + 4 + 1 = 13;110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27;
1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*20 = 32 + 8 = 40.
Поскольку 13 + 27 = 40, двоичное сложение выполнено верно.
Слайд 26 Процесс образования суммы по разрядам описан ниже: а) разряд
1: 12 + 12 = 102; 0 остается в
разряде 1, 1 переносится в разряд 2; б) разряд 2: 02 + 12 + 12 = 102, где вторая 12 – единица переноса; 0 остается в разряде 2, 1 переносится в разряд 3; в) разряд 3: 12 + 02 + 12 = 102, где вторая 12 – единица переноса; 0 остается в разряде 3, 1 переносится в разряд 4; г) разряд 4: 12 + 12 + 12 = 112, где третья 12 – единица переноса; 1 остается в разряде 4, 1 переносится в разряд 5; д) разряд 5: 12 + 12 = 102; где вторая 12 – единица переноса; 0 остается в разряде 5, 1 переносится в разряд 6. Таким образом: 1 1 0 12 +1 1 0 1 12 = 10 1 0 0 02.Слайд 27 Правила умножения Таблица умножения двоичных цифр приведена ниже (обозначения
строк и столбцов соответствуют слагаемым):
Слайд 28 Пример 2. Перемножить двоичные числа 101 и 11. Запишем
множители в столбик и пронумеруем разряды, присвоив младшему разряду
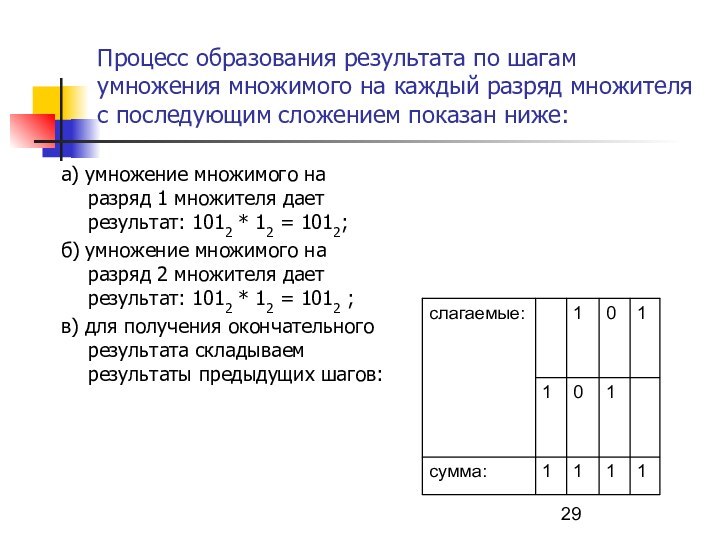
номер 1:Слайд 29 Процесс образования результата по шагам умножения множимого на
каждый разряд множителя с последующим сложением показан ниже:
а) умножение
множимого на разряд 1 множителя дает результат: 1012 * 12 = 1012;б) умножение множимого на разряд 2 множителя дает результат: 1012 * 12 = 1012 ;
в) для получения окончательного результата складываем результаты предыдущих шагов: