отрицается о реальных предметах, их свойствах и отношениях между
ними.Высказывание может быть истинно или ложно.
*
Логика - это наука о формах и способах мышления.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





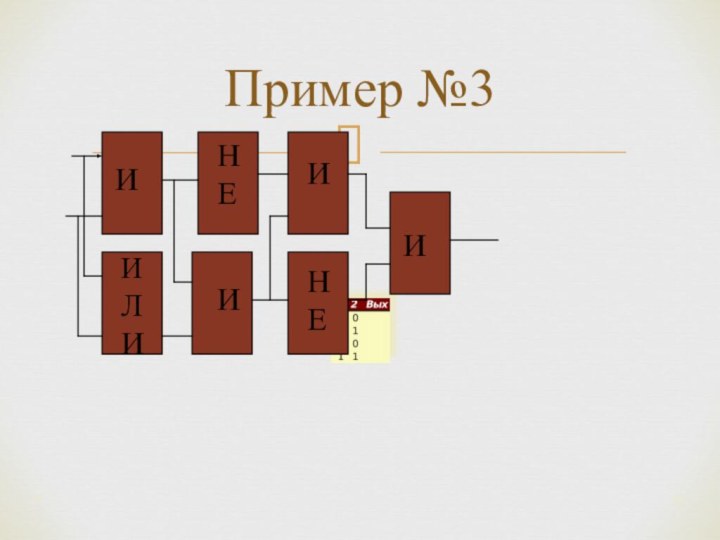
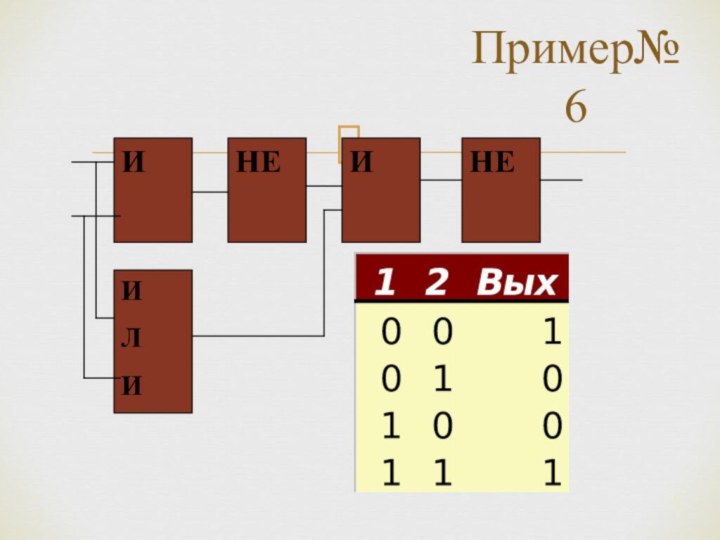
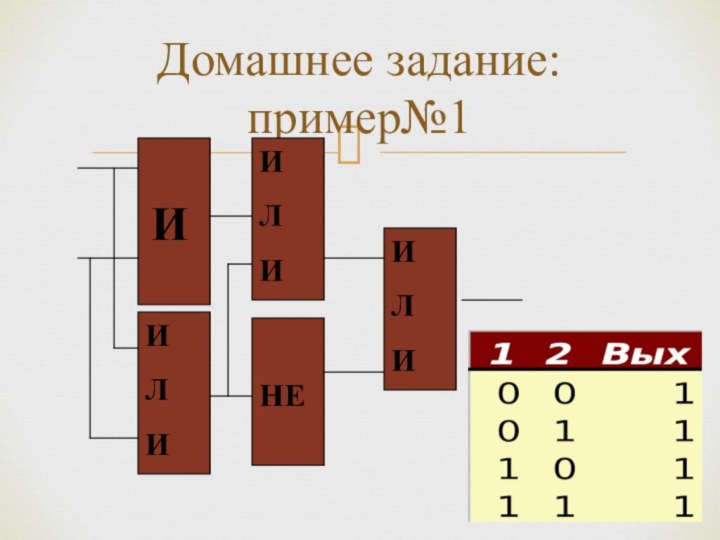
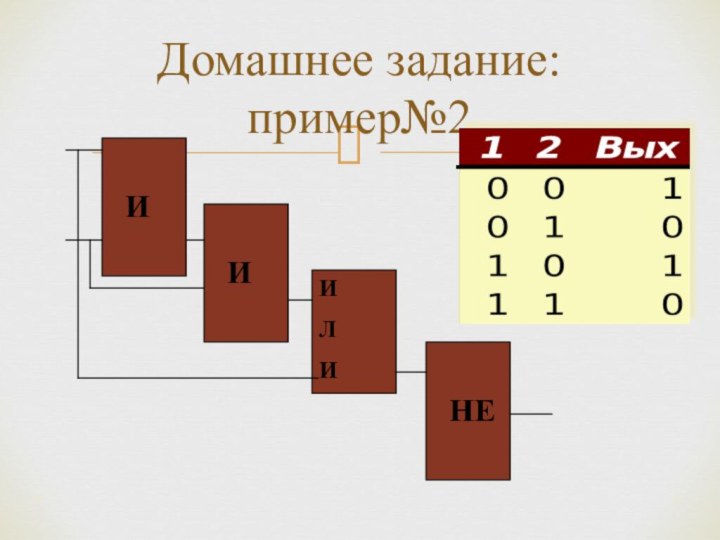
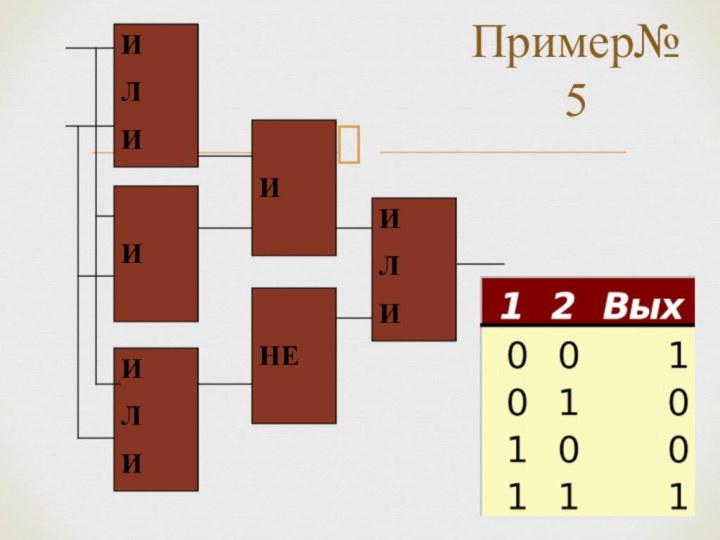
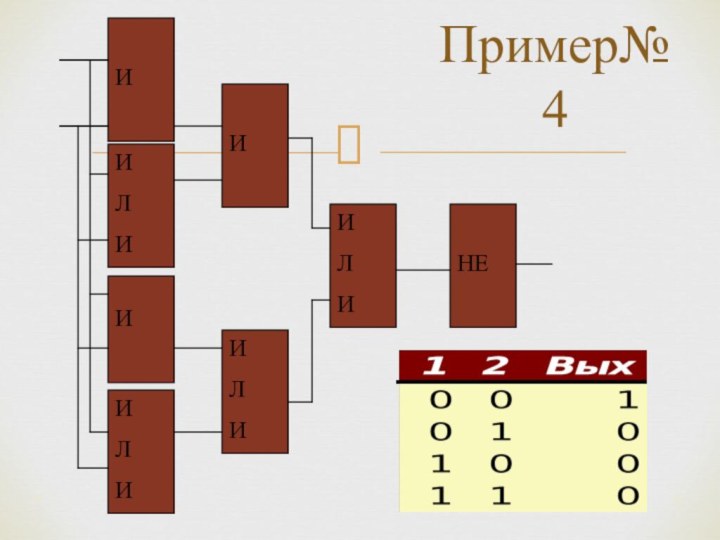
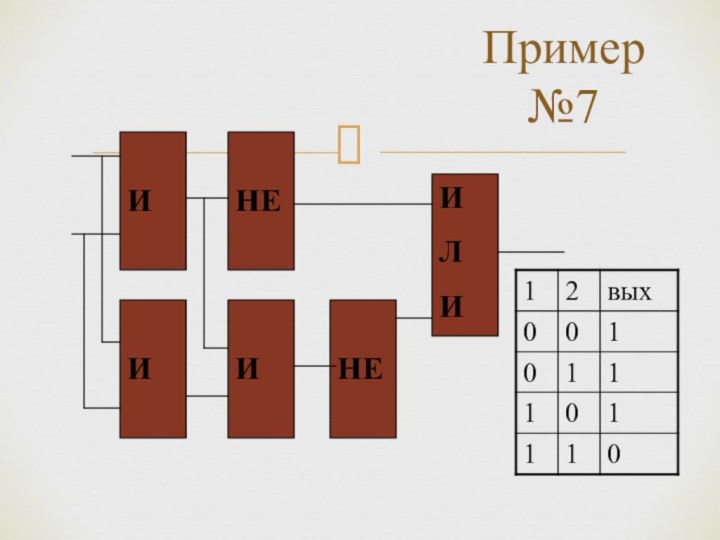
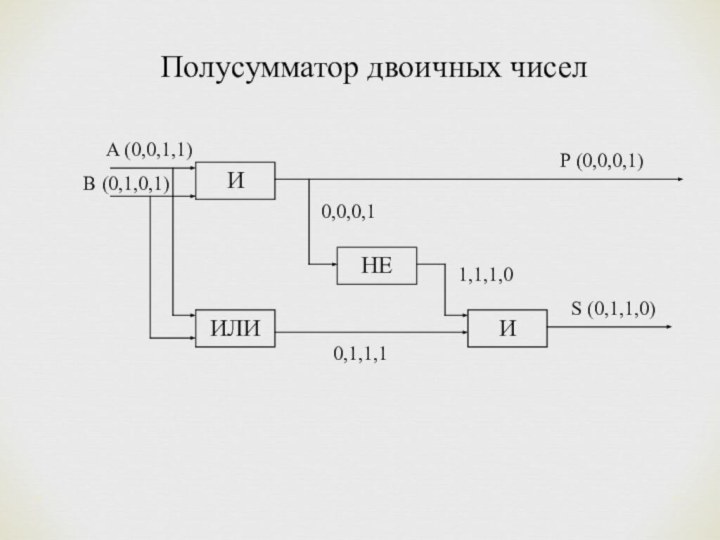

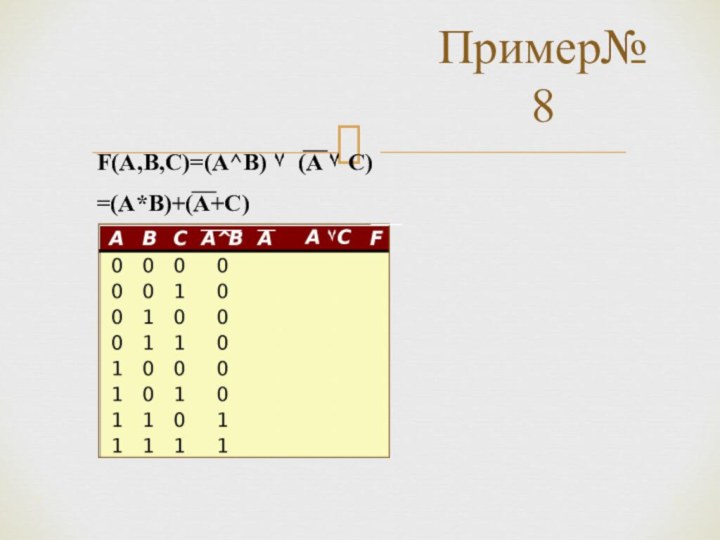
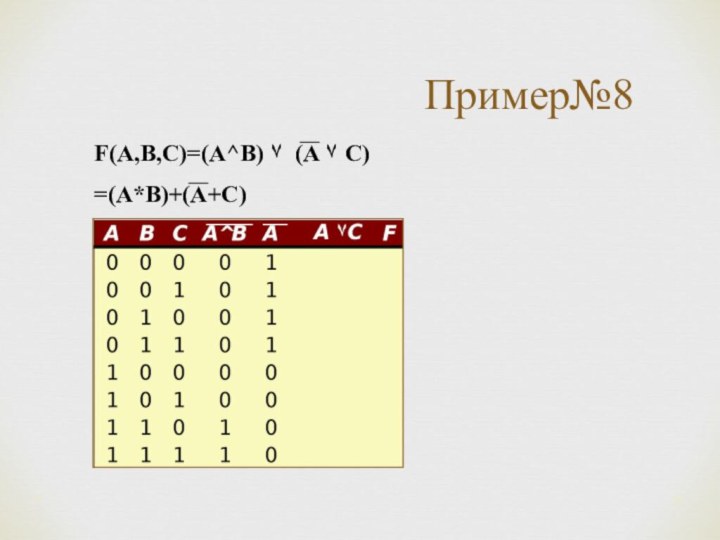
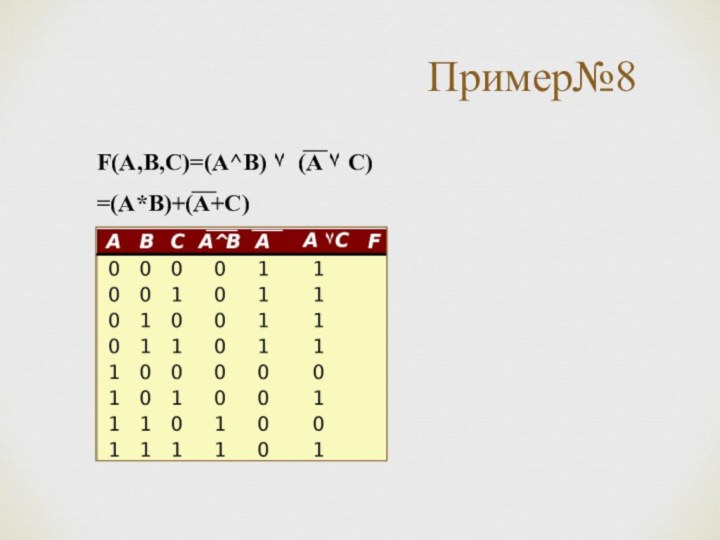
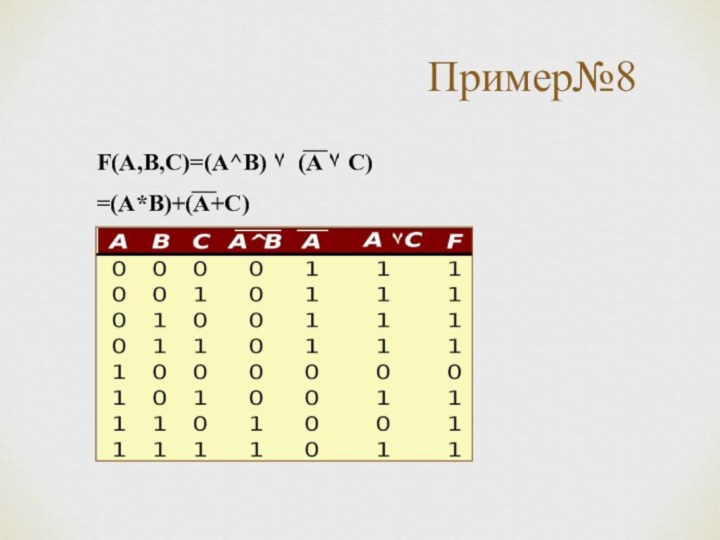




*
Логика - это наука о формах и способах мышления.
*
*
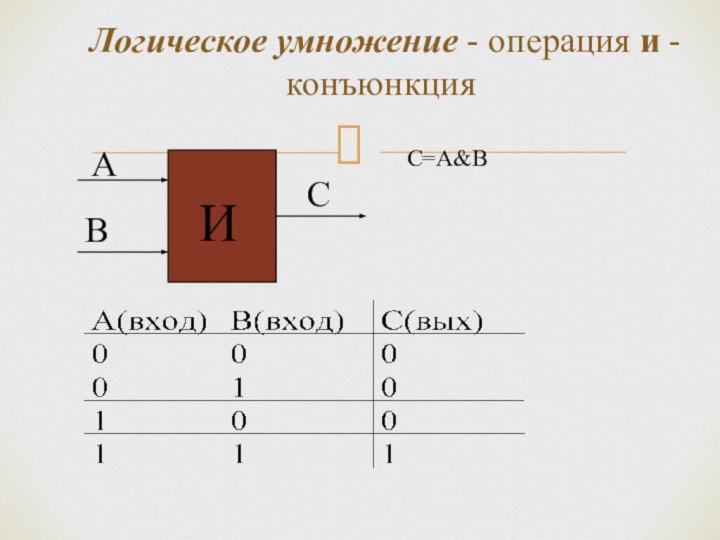
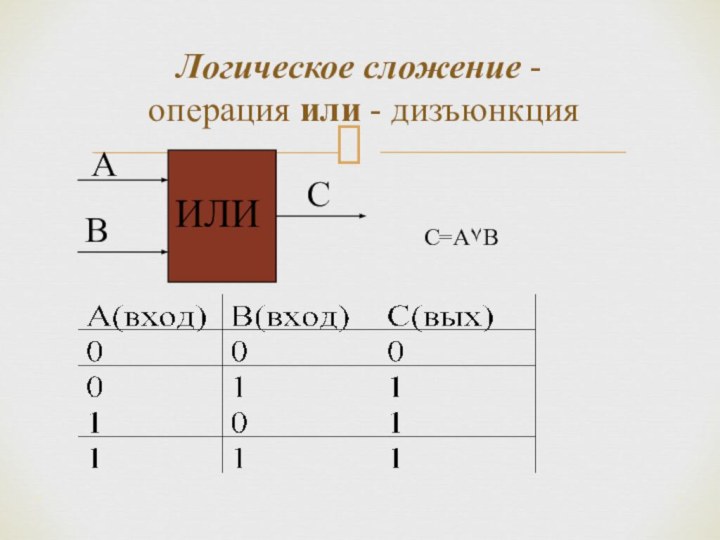
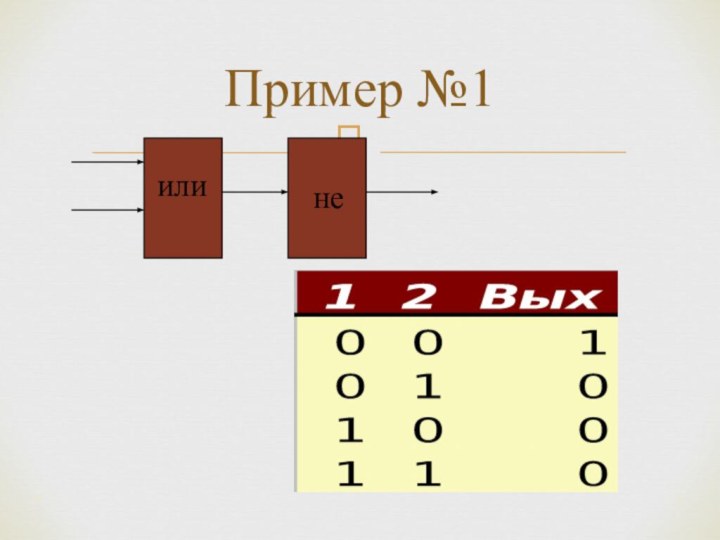
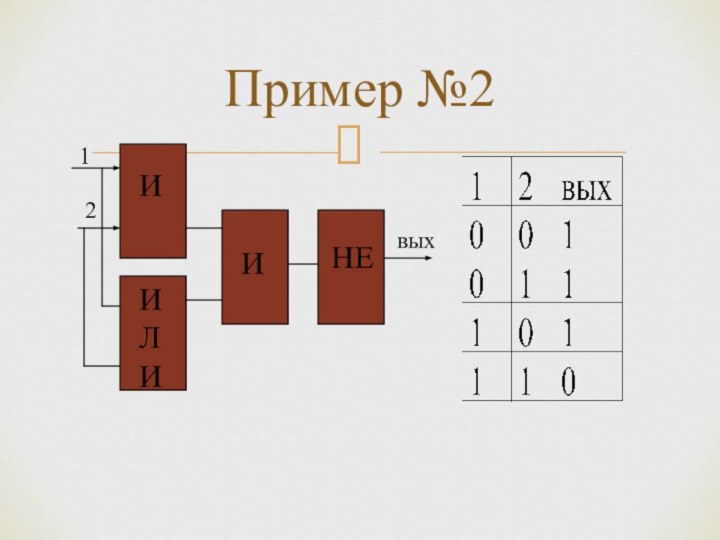
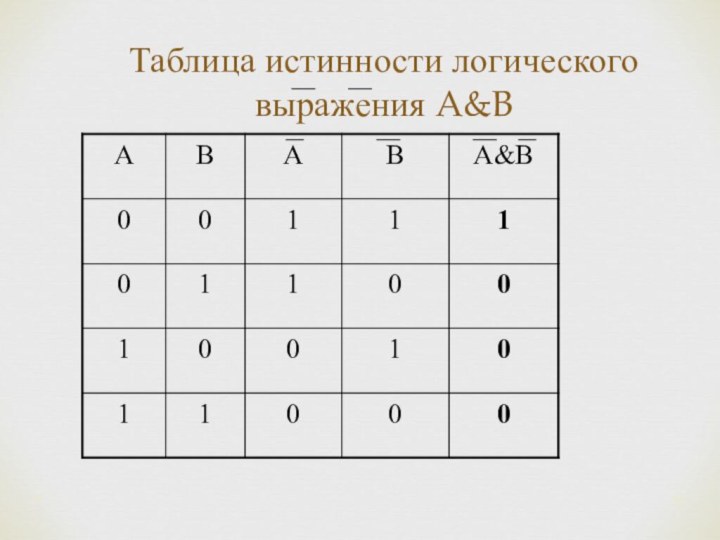
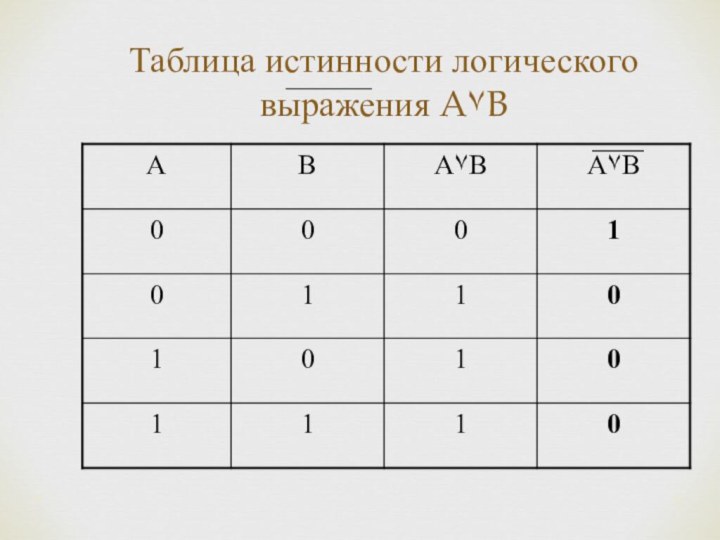
Для образования новых высказываний используются базовые логические операции:
*
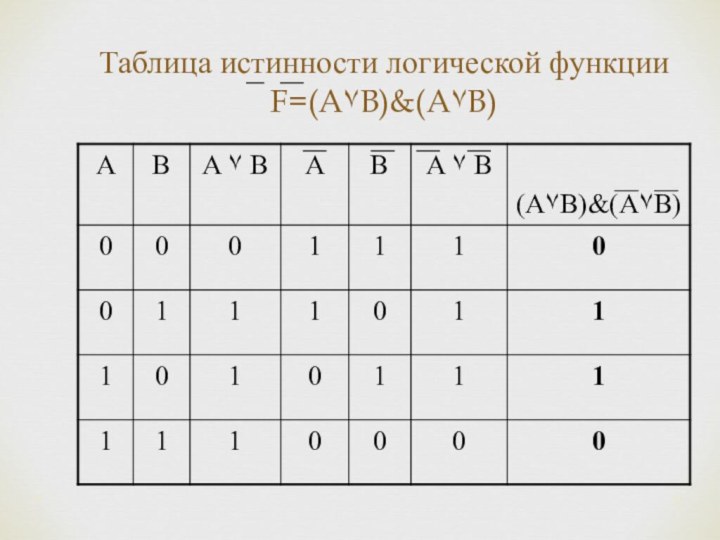
Логические законы и правила преобразования логических выражений
*