- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему MSC.Dytran - 05
Содержание
- 2. СОДЕРЖАНИЕОсновные положенияДискретизация массыВычислительный циклЯвная схема интегрированияВычисление напряжений и сил
- 3. ОСНОВНЫЕ ПОЛОЖЕНИЯДискретизация пространственного объекта с помощью конечных
- 4. МЕТОД ДИСКРЕТИЗАЦИИ МАССЫИнерционные свойства элементов представляются сосредоточенными
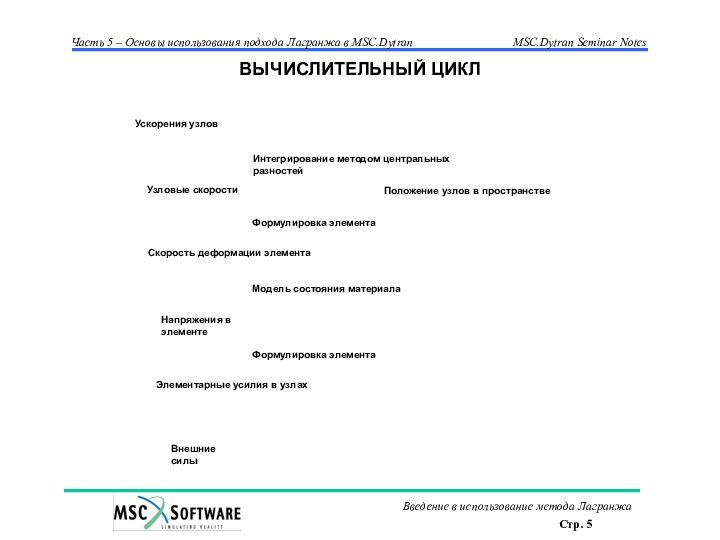
- 5. ВЫЧИСЛИТЕЛЬНЫЙ ЦИКЛ
- 6. ЯВНАЯ СХЕМА ИНТЕГРИРОВАНИЯУскорение узлов вычисляется по формуле
- 7. ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И СИЛЗначения переменных при t=tn
- 8. Скачать презентацию
- 9. Похожие презентации
СОДЕРЖАНИЕОсновные положенияДискретизация массыВычислительный циклЯвная схема интегрированияВычисление напряжений и сил






Слайд 2
СОДЕРЖАНИЕ
Основные положения
Дискретизация массы
Вычислительный цикл
Явная схема интегрирования
Вычисление напряжений и
сил
Слайд 3
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Дискретизация пространственного объекта с помощью конечных элементов
Объёмные
(3D) элементы
Оболочечные (2D) элементы
Стержневые (1D) элементы
Дискретные элементы – пружины,
демпферы и жёсткие телаСетка “скреплена” с материалом и движется вместе с ним; элементы деформируются при деформировании материала
Лагранжевы элементы имеют неизменную массу
Конечные элементы сопрягаются друг с другом посредством общих узлов
Скорость движения материала определяется скоростью движения узлов
Силы прилагаются к узлам
Напряжения определяются (вычисляются) в центре элемента
Слайд 4
МЕТОД ДИСКРЕТИЗАЦИИ МАССЫ
Инерционные свойства элементов представляются сосредоточенными массами
в узлах
Силы прикладываются к узлам
Инерционные силы
Силы упругости деформированных элементов
Внешние
силыСилы взаимодействия
Моментные силовые факторы также вычисляются для узлов с 6 степенями свободы
Слайд 6
ЯВНАЯ СХЕМА ИНТЕГРИРОВАНИЯ
Ускорение узлов вычисляется по формуле
M · an = Fext - Fint
где M – матрица масс;
Fext – внешние нагрузки;
Fint – внутренние силы, “генерируемые” элементами
Матрица M – диагональная
Нет необходимости в обращении матриц, т.к. уравнения независимы:
an =(Fext - Fint)/m
где m – масса, относящаяся к узлу
“Продвижение” во времени выполняется с использованием метода центральных разностей
Вычисляются скорости узлов в момент времени n+1/2
Vn+1/2 = Vn-1/2 + an (Δtn+1/2 + Δtn-1/2)/2
Вычисляются координаты узлов в момент времени n+1
dn+1 = dn + Vn+1/2 Δtn+1/2
Слайд 7
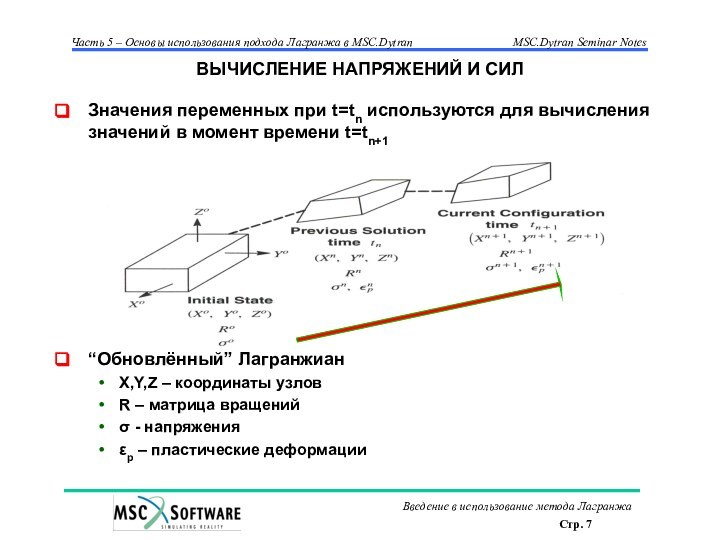
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И СИЛ
Значения переменных при t=tn используются
для вычисления значений в момент времени t=tn+1
“Обновлённый” Лагранжиан
X,Y,Z –
координаты узловR – матрица вращений
σ - напряжения
εp – пластические деформации





























