Слайд 3
Теории аэродинамики
Нелинейно вязкая, сжимаемая среда
Навье-Стокса
Модель турбулентности
“CFD” - вычислительная
гидродинамика
Нелинейная, невязкая, сжимаемаемая среда
Эйлера
Безвихревая, невязкая, сжимаемая среда
Теория потенциала: панельный
метод
Теория тонкого тела
Слайд 4
Теория тонкого тела
Теория тонкого тела – это упрощенная
теория потенциала.
Допускается что тело вызывает только малые, вдоль
оси х, возмущения в равномерном потоке.
Возмущение скорости, которое было внесено в невозмущенный поток, является причиной возникновения скорости касательной к поверхности тела, называемой normal wash (перпендиккулярный поток) или downwash (скос потока вниз).
Слайд 5
Аэродинамическая теория в MSC.Nastran
Все аэродинамические теории в MSC.Nastran
основываются на теории тонкого тела.
Стандартные методы
Метод дипольных решеток (DLM)
для дозвуковых задач
Метод гармонического градиента (Зона51) для сверхзвуковых задач
Слайд 6
Метод дипольных решеток
Линия диполей
Точка скоса потока
Только несущие поверхности
+
тонкое тело
Слайд 7
Метод Зона51
Линия Маха
Постоянное давление
Точка скоса потока Зона51
Слайд 8
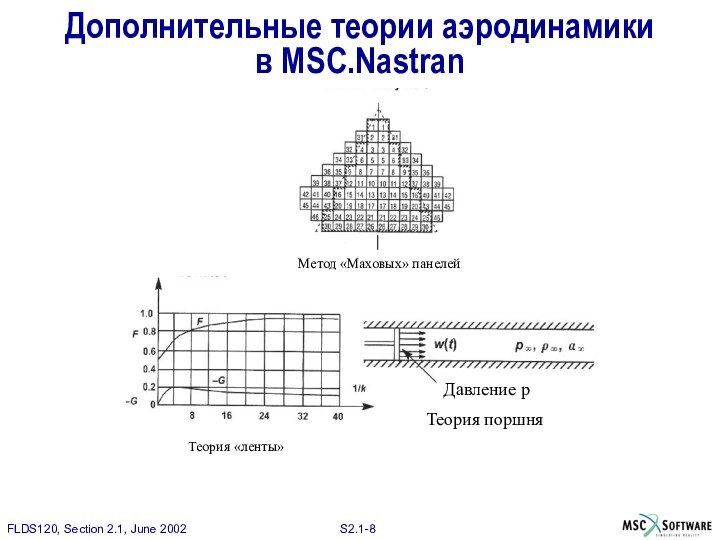
Дополнительные теории аэродинамики в MSC.Nastran
Давление р
Теория поршня
Метод «Маховых»
панелей
Теория «ленты»
Слайд 9
Приведенная частота
Приведенная частота это ключевой параметр в нестационарной
аэродинамике
Определяется как
Где
циклическая частота колебаний
относительная длина
скорость полета
приведенная скорость
расстояние пройденное за один период колебания
Слайд 10
Основные аэродинамические матрицы
Матрица коэффициентов аэродинамического влияния может быть
найдена через скос потока и коэффициент давления
Основная матрица дифференциалов
– через скос потока и перемещения
Матрица интеграллов – через аэродинамические нагрузки и коэффициент давления
Слайд 11
Матрица аэродинамической жесткости
Матрица аэродинамической жесткости определяется через аэродинамические
нагрузки и перемещения
Она может быть вычислена через три основные
матрицы
Слайд 12
Метод дипольных решеток: источники
Метод дипольных решеток – это
расширенный метод стационарных вихревых решеток для колеблющегося потока.
Источники:
Hedman,
S. G., "Vortex-Lattice Method for Calculation of Quasi-Steady State Loadings on Thin Elastic Wings," Aeronautical Research Institute of Sweden, Report 105, October 1965.
Albano, E. and Rodden, W.P. A Doublet Lattice Method for Calulating Lift Distributions on Oscillating Surfaces in Subsonic Flows. AIAA J., Vol. 7 No. 2, pp. 279-285, 1969, and Vol. 7, No. 11, p. 2192, 1969
Rodden, W.P., Taylor, P.F. and McIntosh, S.C., Further Refinement of the Subsonic Doublet-Lattice Method, AIAA J. Vol. 35, No. 5, 1998
Blair, Max, A Compilation of the Mathematics Leading to the Doublet-Lattice Method, NASA Report WL-TM-95-302, 1994
Слайд 13
Метод дипольных решеток (МДР)
МДР может быть использован для
расчета несущих поверхностей в дозвуковом потоке.
Предполагается что все несущие
поверхности расположенны чуть-чуть не параллельно потоку, из-за наличия малых возмущений. Используется линейная аэродинамическая теория.
Каждая несущая поверхность делится на мальнькие трапецеидальные элементы (панели).
Панели располагаются в форме ленты (одна за другой), параллельной направлению скорости свободного потока.
Линии перегиба и шарнирые линии необходимо располагать на границе панелей.
Опция симметрии необходима для уменьшения размерности задачи.
Слайд 14
Метод дипольный решеток: теория
Метод дипольных решеток получен путем
дискретизации интегрального выражения.
Дискретное уравнение
где подинтегральная функция получена из
нестационарной дозвуковой теории аэродинамики.
Интеграл вычисляется с помощью высокоточной аппроксимации подинтегральной функции.
Слайд 15
Метод дипольный решеток : интегрирование
Исходный програмный код МДР
использует порабольческую апроксимацию подинтегральной функции. Она обозначается N5KA.
В MSC.Nastran
70.6 была применена высокоточная аппроксимация 4-й степени. Она обозначается N5KQ.
Апроксимация 4-й степени выбирается путем установки системной переменой cell 270 (QUARTICDLM) в значение 1. Пораболическая аппроксимация используется по умолчанию.
Слайд 16
Метод дипольных решеток: опция N5KQ
Эта опция обеспечивает высокоточную
аппроксимацию разброса значений подинтегральной функции .
Сравнение действительной части коэффициентов
подъемной силы.
Отношение геометрических размеров панели (Box Aspect Ratio ) = 10.0
Слайд 17
Метод дипольных решеток
Принципы моделирования
Обозначение аэродинамических панелей начинается с
названия макроэлемента обозначенного CAERO1 и возрастает на единицу для
последующей.
Обозначение следует сначала вдоль потока а потом вдоль размаха крыла
Нумерация аэродинамических узлов производится независимо от нумерации структурных узлов, скалярных и особых точек, так что допускается дублирование номеров структурной и аэродинамической моделей.
Аэродинамические узлы не могут иметь одинаковые обозначения
Панель. Номер панели = CAERO_ID + 0 … n
Угловой узел
Номер узла =
CAERO_ID +0 ... n
Макроэлемент или “CAERO”
Слайд 18
Метод дипольных решеток
Принципы моделирования
Угловому узлу аэродинамической панели присаивается
наименьший номер из (NCHORD+1) x (NSPAN+1). При создании второй
аэродинамической сетки, порядок номеров возрастает на 1000. Рекомендованный порядок нумерации автоматически выполняется во Flightloads.
1-я аэродинамическая
сетка
2-я аэродинамическая
сетка
Слайд 19
Метод дипольных решеток
Принципы моделирования
Панели обозначаются как k-множество степеней
свободы. Каждая панель имеет 2 степени свободы.
Одна панель представляет
собой тонкую пластину траппецевидной формы. Два ребра должны быть обязательно параллельны направлению потока.
Одно параллельное ребро может быть вырождено в точку.
Панели могут иметь отношение геометрических разммеров меньше 3 при использовании аппроксимации N5KA и меньше 6 при N5KQ. Возможно, что в зависимости от конфигурации, большие отношения геометрических параметров могут быть использованы в N5KA и N5KQ. При использовании больших значений рекомендуется исследовать сходимость.
N5KA используется по умолчанию. N5KQ может быть активирован при помощи NASTRAN команды: NASTRAN QUARTICDLM = ON
Слайд 20
Метод дипольных решеток
Принципы моделирования
Пусть будет число панелей в
длине волны минимум 12,5. Число панелей в длине волны:
Однако,
должно быть использованно не меньше 4-х паннелей и рекомендуется всегда исследовать сходимость результатов. Во Flightloads эти расчеты будут выполняться самостоятельно.
Δx < 0.08 v / f
Панели должны быть сконцентрированы в области неоднородности среды, таких например как передняя кромка крыла, кромка оперения и линия шарнира.
Используйте узкие панели на конце крыла, где нагрузка уменьшается.
Доступные группы аэродинамической интерференции снижают затраты времени на генерацию матриц и изучение влияния поверхностей друг на друга.
v = скорость
Слайд 21
Метод дипольных решеток
Принципы моделирования
В случае сложных почти компланарых
поверхностей не допускайте что бы среднии линии одних панелей
находились на одной линии с ребрами других панелей
НЕ ДОПУСКАЕТСЯ!
Слайд 22
Зона51
Зона51 может быт использована для расчета несущих поверхностей
в сверхзвуковом потоке
Эта опция в MSC.Nastran называется Aeroelasticity II.
Вычисляется матрица [Ajj]
Теория метода Зона51 описа в ниже приведенных источниках:
Chen, P. C. and D. D. Liu, "A Harmonic Gradient Method for Unsteady Supersonic Flow Calculations," Journal of Aircraft, Vol.22, No. 5, May 1985, pp. 371-379.
Liu, D. D., D. K. James, P. C. Chen, and A. S. Pototsky, "Further Studies of Harmonic Gradient Method for Supersonic Aeroelastic Applications," Paper 89-068, DGLR/AAAF/RAeS European Forum on Aeroelasticity and Structural Dynamics, Aachen, FRG, 17-19 April 1989.
Предполагается что все несущие поверхности расположенны чуть-чуть не параллельно потоку, из-за наличия малых возмущений. Используется линейная аэродинамическая теория.
Каждая несущая поверхность делится на мальнькие трапецеидальные элементы (панели).
Слайд 23
Зона51
Панели располагаются в форме ленты, параллельной направлению скорости
свободного потока.
Линии перегиба и шарнирые линии необходимо располагать
на границе панелей.
Опция симметрии необходима для уменьшения размерности задачи.
Эффектом толщины пренебрегают, но можно будет приближенно посчитать коэффициеты коррекции, используя теорию сверхзвукового аэродинамического профиля второго порядка.
Слайд 24
Зона51.Теория
Для сверхзвуковых скоростей
Неизвестное давление принимается как постоянное для
каждой панели
Известные условия скоса потока заданы на расстояниии 95%
от длины хорды панели в центре пролета.
В MSC.Nastran аэродинамический узел задается на средней хорде в середине пролета
Линия Маха
Постоянное давление
Скос потока, расположенный в точке находящейся на расстоянии 95% от носка панели
Слайд 25
Зона51.Теория
Для n панелей
В матричной форме (как и в
МДР)
{w} = [A]{Cp}
Интеграл вычисляется при помощи высокоточной аппроксимации подинтегральной функции
Слайд 26
Метод постоянного даления
Эта опция в пакете Aero 1
предназначена для вычисления матрицы Aji при сверхзвуковых расчетах.
Такая же
опция устанавливается для метода Зона51
Такие же принципы принципы
Не часто применялся, поэтому будте осторожны при использовании
Установки:
PARAM, SUPAERO, CMP or ZONA (default).
Источники:
Appa, K and Smith, M.J.C., “Evaluation of the Constant Pressure Panel AIAA/ASME/ASCE/AHS 29th Structures, Structural Dynamics and Materials Conference, Williamsburg Virginia, April 1988.
Слайд 27
Дозвуковое крыло – теория интерференции тел
Теория тонкого тела
для изолированного тела имеет большую историю. Существует свыше двухсот
статей по этой тематике, список литературы можно посмотреть в журнале
Revell, J. D., "Second-Order Theory for Steady or Unsteady Subsonic Flow Past Slender Lifting Bodies of Finite Thickness," AIAA Journal, Vol. 6, No. 6, June 1969, pp. 1070-1078.
В применяемой теории тонкого тела отображаются несущие характеристики каждого тела. Нагрузка пропорциональна коэффициенту площади поперечного сечения.
Взаимное влияние тел использует метод суперпозиции сингулярностей и их подобия.
Тела имеют продольную (y) и вертикальную (z) степень свободы.
Первоначально интерференция крыло-тело расчитывалась для систем подобия с вихрями из МДР и диполями на цилиндрическом интерференционном теле, описанном как узкое тело (Метод подобия Гисенга).
Слайд 28
Дозвуковое крыло – теория интерференции тел
Однородное уравнение для
скоса потока
где ww = скос потока на панели крыла
расположенный на расстоянии 0.75 длины хорды от носка
wl = 0 = скос потока для инетерферирующих элементов вносит сингулярность одних тонких элементов на другие
ws = скос потока для элемента узкого тела
Cw = силы, расположенные вдоль панели крыла на расстоянии 0.25 хорды
μr = диполи остаточного течения
μs = диполи тонкого тела
Слайд 29
Дозвуковое крыло – теория интерференции тел
Уравнение для силовых
факторов
где Sww = площадь панели
G, Ssw Ssr Sss = матрицы, использующиеся для получения массовых сил (смотри раздел 2.6.3 of Giesing, J.P., Kalman, T.P., and Rodden, W.P., "Subsonic Unsteady Aerodynamics for General Configurations; Part II, Vol. 1, - Application of the Doublet-Lattice method and the Method of Images to Lifting-Surface/Body Interference," Air Force Flight Dynamics Laboratory Report No. AFFDL-TR-71-5, Part II, Vol. 1, April 1972)
Слайд 30
Дозвуковое крыло – теория интерференции тел
Рисунок 3-1a. Изображены
панели и элементы тонких тел. N5KA Бомбардировщик. 3 поверхности,
10 панелей
Слайд 31
Дозвуковое крыло – теория интерференции тел
Рисунок 3-2b. Изображены
интерфереционные элементы. N5KA Бомбардировщик 3 поверхности, 10 панелей, 2
тела, 9 тонкотельных элементов и 7 интерфереционных элементов