Презентация на тему Представление чисел в памяти компьютера

виде двоичных кодов. Отдельные элементы двоичного кода, принимающие значение

0 или 1, называют разрядами или битами. Память компьютера условно делиться на отсеки или ячейки, каждая из которых имеет свой номер. Нумерация начинается с нуля.
Минимальной адресуемой ячейкой памяти называется байт – 8 двоичных разрядов. порядковый номер байта называется его адресом.
Наибольшую последовательность битов, которую процессор может обрабатывать как единое целое, называют машинным словом.
Длина машинного слова может быть разной - 8 , 16 , 32 бит и т.д. Двоичные разряды в любой ячейке памяти нумеруются справа налево, начиная с нуля.
Существуют два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, второй (так называемое представление числа в формате с плавающей точкой) используется для задания некоторого подмножества действительных чисел.
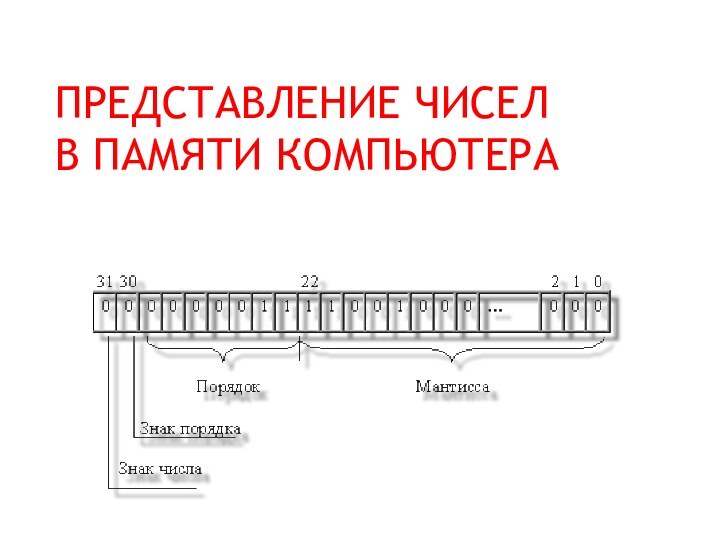
Для положительных и отрицательных чисел существует знаковый способ представления числа. Под знак отводится старший разряд ячейки:
0 - для положительных чисел,
1 - для отрицательных чисел.

числа представляются специальными кодами - прямым, обратным и дополнительным.

Для

положительного числа прямой, обратный и дополнительный коды
выглядят одинаково.

Прямой код двоичного числа — это само двоичное число, причем значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел -1 .
Обратный код отрицательного числа получается из прямого кода путем замены нулей единицами, а единиц нулями, исключая знаковый разряд.
Дополнительный код отрицательного числа образуется как результат суммирования обратного кода с единицей младшего разряда. Перенос в знаковый разряд при этом теряется.

Примечание. Дополнительный код основан на понятии дополнения числа - величины, которую надо добавить к числу, чтобы получить переход единицы в старшем разряде.

Дополнением k-разрядного целого числа Z в системе счисления с основанием q называется величина:
D = q k - Z.

следующих двоичных чисел:
а)100100; б) -100011; в) -100100.
Решение
Будем считать, что

число размещается в двух байтах. Старший бит – знак разряда. Незначащие нули добавляются слева от числа. Результат представим в виде таблицы:

целое число 1234510 ?

Решение
Для размещения числа возьмем два байта.
Поскольку

число положительное, то в старшем (15-м) бите будет 0.
Переведем число в двоичную систему счисления:
1234510 = 110000001110012.
Результат:

Знак числа число

в однобайтовом формате:
а) 64

б) 58 в) 72 г) -96

2. Запишите двоичные числа в дополнительном коде:
а) 1010 б) -1001 в) -11 г) -11011

3. Переведите в прямой код числа, записанные в дополнительном коде, и найдите их десятичные эквиваленты:
а) 00000100 б) 11111001

4. Представьте целые числа в 16-разрядной ЭВМ:
а) 25 б) -25 в) 801 г) -610

вычитания и умножения двоичных чисел, наиболее подходящие для аппаратной

реализации.
Целочисленная двоичная арифметика используется при изучении программирования, в процессе освоения операторов цикла, оператора выбора, стандартных процедур val и str, операций над целыми числами div и mod, операций над строковыми величинами.
Сложение чисел производится в дополнительных кодах поразрядно. При выполнении арифметических операций число может выйти за указанные границы. Произойдет переполнение разрядной сетки, поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта.
Чтобы избежать ситуации переполнения, в языках программирования предусмотрено строгое описание типа переменной, которым определяется набор возможных ее значений.
Вычитание целых чисел эквивалентно сложению с отрицательным числом. Отрицательное число может быть представлено в прямом коде. Однако использование прямого кода усложняет структуру команд процессора. При выполнении сложения чисел с разными знаками требуется выбрать из них большее по модулю, затем вычесть из него меньшее, выяснить знак большего и присвоить этот знак остатку. По этой причине в компьютерах используется представление отрицательного числа в дополнительном коде. Таким образом, операция вычитания выполняется как сложение с дополнительным кодом вычитаемого.

с использованием итерационных алгоритмов (ряда повторяющихся шагов).
Умножение двоичных чисел

сводится к двум операциям: сложения и сдвига.
Операция деления для целых чисел однозначно не определена, поскольку в общем случае приводит к появлению нецелых (вещественных) чисел. Существуют различные методы и алгоритмы реализации этой операции в разных процессорах.
Пример 1. Выполнить операцию вычитания 25 -34 .
Учтем, что 25-34 = 25+ (-34) .
Переведем числа 25 и 34 в двоичную систему счисления:
2510 = 110012 и 3410 = 1000102 .
Запишем прямые, обратные и дополнительные коды, воспользовавшись 8-разрядной сеткой:

После сложения дополнительных кодов получим код 11110111. Единица в старшем бите полученного кода означает, что число отрицательное. Следовательно, результат надо перевести в обратный, а затем в прямой код:
11110111 -> 10001000 -> 10001001 .
Полученный результат интерпретируется как десятичное число:-10012= -910 .

памяти машины абсолютно точно, значения вещественных чисел являются приближенными.

В некоторых областях вычислений требуются очень большие или малые действительные числа. Для получения большей точности применяют запись чисел с плавающей точкой.
В общем случае в формате с плавающей точкой число представляется в виде произведения двух сомножителей: R=m*Pn
где m -мантисса числа;
Р - основание системы счисления;
n - порядок, указывающий, на какое количество позиций и в каком направлении должна сместиться точка, отделяющая дробную часть в мантиссе.
Например, число 5,14 может быть записано 0,514∙101 или 51,4∙10-1 и т.д. Запятая (десятичная точка) перемещается, или «плавает», вправо и влево в зависимости от порядка числа.
При работе с числами в языках программирования и вычислительных системах используется экспоненциальная форма записи:

R = m∙E±n,

где Е - десятичное основание системы.
Например, 3,1467890000Е + 2 = 314,6789
Нормализованная мантисса меньше единицы и первая значащая цифра не ноль.

б) 218,4785∙10-3 и 1847,85∙10-4;

2. Запишите числа в естественной форме:
а) 0,1100000∙2100; б) 0,1001111∙2-111;

3. Выполните действия:
а) 0,101010∙211 + 0,110011∙2100;
б) 0,100011∙2100 – 0,100001∙2100;
в) 0,110011∙2-10 * 0,100001∙21;
г) 0,101001∙210 / 0,100000∙210.

хранение двух чисел: мантиссы и порядка. Чем больше разрядов

отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон чисел, представимых в машине при заданном формате.
Правила кодирования мантиссы и порядка отличаются для различных типов машин.
Рассмотрим для начала один из вариантов представления вещественных чисел.
Для размещения вещественного числа могут использоваться четыре байта (32 бита) - короткий формат, 8 байтов длинный формат, 16 байтов - формат повышенной точности. В любом случае старший байт остается постоянным, а изменяется область, отведенная под мантиссу. Старший байт включает в себя:
один бит (старший) - знак числа;
один бит - знак порядка;
шесть битов - порядок числа.
В таком представлении максимальный порядок числа равен 1111112 = 6310. Следовательно, 1063 - максимальное число, которое можно закодировать таким образом:

порядок мантисса
знак порядка
знак мантиссы

число —123,4510 ?
Решение
Представим число в 4 байтах.
Нормализованный вид: -0,12345∙103

.
Число отрицательное, поэтому старшим (31-й) бит равен 1.
Порядок равен 3, он положительный, значит, З0-й бит равен 0.
Число 3 в двоичной системе счисления имеет вид 11. Чтобы записать его в оставшихся 6 битах старшего байта, необходимо добавить незначащие нули.
Таким образом, старший байт имеет вид: 10000011 .
Найдем двоичное представление мантиссы 0,12345 по алгоритму перевода дробной части, 24 раза умножив ее на 2.
Результат:

Пример 2. Раскодировать содержимое четырех байтов памяти: а) как два целых числа; б) как одно вещественное:

Решение
а) 17793;-128;
б) приблизительно 0,5058593 • 10-3 (порядок записан в дополнительном коде).

вещественных чисел. Поэтому во многих современных компьютерах используют не

прямое значение порядка, а смещенное. Его называют характеристикой числа. Для разных типов ЭВМ существуют разные варианты смещения порядка. Рассмотрим один из вариантов.
Запись вещественного числа имеет структуру следующего вида:
n-1 n-2

Знак мантиссы Смещенный порядок Абсолютная величина мантиссы

Здесь порядок n-разрядного нормализованного числа задается в смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка прибавляют смещение, равное 2k-1.
Например, порядок, принимающий значения в диапазоне от -64 до +63, представляется смещенным порядком, значения которого меняются от 0 до 127.
Прокомментируем этот случай. В семи двоичных разрядах помещаются двоичные числа от 0000000 до 1111111. В десятичной системе счисления это числа от 0 до 127. Всего 128 значений, которые разделяются поровну между положительными и отрицательными значениями порядка в диапазоне от -63 до 63.
Связь между смещенным порядком S и математическим Р в данном случае выражается формулой: S = Р + 6410 = P + 100 00002.

форме с плавающей точкой в 4-х байтовом машинном слове.
Решение:
1.

Переведем число в двоичную систему счисления с 24 значащими цифрами (3 байта под мантиссу):
250.187510= 11111010,00110000000000002.
2. Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,111110100011000000000000∙1010002. Здесь мантисса, основание системы счисления (210 = 102) и порядок (810 = 10002) записаны в двоичной системе.
3. Вычислим характеристику: S2 =1000 + 1000000 = 1001000.
4. Запишем представление числа в 4-байтовой ячейке памяти с учетом знака числа:


Шестнадцатеричная форма: 48FA3000.

гораздо сложнее целочисленной арифметики. Для некоторых процессоров (в частности

Intel) операции над вещественными числами вынесены в отдельный узел, который называют математическим сопроцессором.
Сложение чисел с плавающей запятой выполняется в соответствии со следующим алгоритмом.
1. Представить числа А и В в нормализованном виде, записав отдельно значения мантисс и порядков.
2. Выровнять порядки по числу с большим порядком.
3. Выровнять число цифр в мантиссах по числу, порядок которого не изменился.
4. Сложить числа.
5. Нормализовать сумму, оставив число цифр в мантиссе таким, как у числа, порядок которого не изменялся.