Слайд 2
Раздел 2. Моделирование для динамического анализа
КОМПОНЕНТЫ ВХОДНОГО ФАЙЛА
MSC.Nastran……………….………… 2 - 3
ФОРМАТ РАДЕЛА BULK DATA ВХОДНОГО ФАЙЛА
MSC.Nastran.……. 2 - 4
КОНЕЧНО-ЭЛЕМЕНТНЫЙ АНАЛИЗ.……………………...…………………… 2 - 5
ОБЫЧНО ИСПОЛЬЗУЕМЫЕ УПРУГИЕ ЭЛЕМЕНТЫ..……………..………. 2 - 6
РАСПРЕДЕЛЕННЫЕ И СОСРЕДОТОЧЕННЫЕ МАССЫ..………...………. 2 - 7
КОНЕЧНЫЙ ЭЛЕМЕНТ ROD.……………………………….…………………… 2 - 9
РАСПРЕДЕЛЕННАЯ МАССА В MSC.Nastran………………………………. 2 - 11
ЕДИНИЦЫ МАССЫ.……………………………………………………………… 2 - 13
ЗАДАНИЕ МАССЫ..……………………………………….……………………... 2 - 14
ЭЛЕМЕНТ CONM2.…………………………………..…………………………… 2 - 16
ОСНОВНЫЕ ОПЕРАЦИИ НАД НАБОРАМИ СТЕПЕНЕЙ СВОБОДЫ В MSC.Nastran………………………………….……………………….……………. 2 - 18
СТЕПЕНИ СВОБОДЫ В MSC.Nastran ...……………………………………… 2 - 19
РЕКОМЕНДАЦИИ ПО ВЕРИФИКАЦИИ МОДЕЛИ..…………………...…….. 2 - 22
Слайд 3
Компоненты входного файла MSC.Nastran
Операторы FMS и NASTRAN –
назначения файлов и задание системных параметров
Executive Control Section –
задание типа решения, выделяемого времени, параметров диагностирования
CEND – оператор - “разделитель”
Case Control Section – формирование перечня выводимых результатов, инициализация некоторых операторов Bulk Data Section
BEGIN BULK - оператор - “разделитель”
Bulk Data Section – описание расчетной модели, параметров решения
ENDDATA - оператор - “разделитель”
Слайд 4
Формат раздела BULK DATA входного файла MSC.Nastran
Формат с
фиксированной длиной поля
GRID^^^^2^^^^^^^3^^^^^^^1.0^^^^^-2.0^^^^3.0^^^^^^^^^^^^^316
“Свободный” формат, этот же оператор
GRID,2,3,1.0,-2.0,3.0,,316
Репликаторы для повторного
ввода
Исходная запись: GRID,1,,0.,0.,0.,,126
=, *(5),=,=,*(1.),==
=(3)
Результат:
В примерах к данному курсу используются свободный формат и репликаторы.
Слайд 5
Конечно-элементный анализ
В реальном мире существуют не только системы
с одной степенью свободы.
Конечные элементы используются для моделирования массы,
демпфирования и жесткости сложных систем и конструкций.
Степени свободы (СС - DOF) – независимые координаты, описывающие перемещения конструкции в любой момент времени.
Узлы GRID используются для дискретного моделирования непрерывной структуры.
Каждый узел GRID может иметь шесть СС: поступательные вдоль осей X, Y и Z и вращательные относительно осей X, Y и Z.
Взаимосвязь перемещений осуществляется путем соответствующих матричных преобразований.
Слайд 6
Обычно используемые упругие элементы
Слайд 7
Распределенная и сосредоточенная массы
Распределенная масса в общем случае
более точно описывает массовые свойства, нежели сосредоточенная.
Сосредоточенная масса предпочтительнее
для вычисления скорости при динамическом анализе.
Задание “распределенной” формулировки матрицы масс
PARAM, COUPMASS, 1 – выбор “распределенной” формулировки
“По умолчанию” – “сосредоточенная” формулировка
Сосредоточенную и распределенную массы могут иметь элементы:
BAR, BEAM, CONROD, HEXA, PENTA, QUAD4, QUAD8, ROD, TETRA, TRIA3, TRIA6, TRIAX6, TUBE
Только сосредоточенную массу могут иметь элементы:
CONEAX, SHEAR
Только распределенную массу могут иметь элементы:
BEND
Слайд 8
Распределенная и сосредоточенная массы
Сосредоточенная масса имеет только диагональные,
поступательные компоненты (вращательных нет).
Распределенная масса имеет как недиагональные поступательные,
так и вращательные компоненты для элементов BAR (за исключением “торсионных”), BEAM и BEND.
Игнорирование инерционных свойств может сказываться на результатах анализа механизмов с малой массой.
Слайд 9
Конечный элемент ROD
Матрица жесткости:
“Классическая” связанная масса:
Слайд 10
Конечный элемент ROD
Сосредоточенная масса в “классической” формулировке (совпадает
с формулировкой MSC.Nastran):
Распределенная масса (формулировка MSC.Nastran):
Поступательные члены соответствуют результату
осреднения сосредоточенной массы и “классической” связанной массы. Такое осреднение признано лучшим для элементов ROD и BAR.
Слайд 11
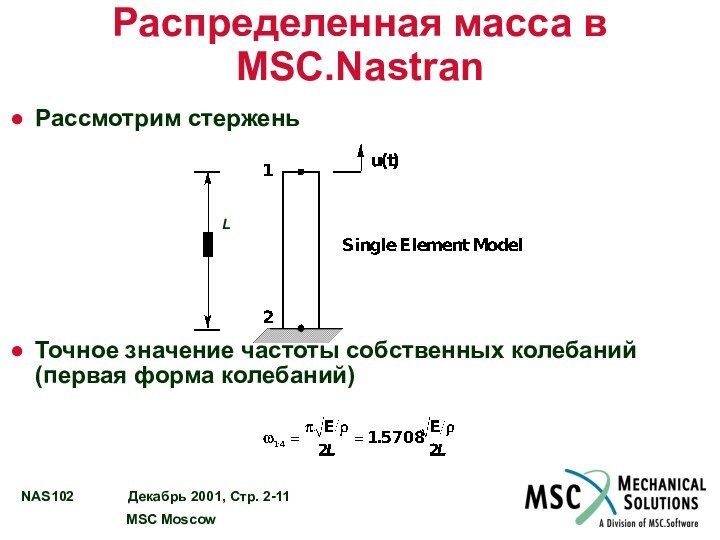
Распределенная масса в MSC.Nastran
Рассмотрим стержень
Точное значение частоты собственных
колебаний (первая форма колебаний)
L
Слайд 12
Распределенная масса в MSC.Nastran
Различные аппроксимации
Сосредоточенная масса
“Классическая” связанная масса
MSC.Nastran
Распределенная
масса
Слайд 13
Единицы массы
MSC.Nastran предполагает согласованность единиц. ВЫ ДОЛЖНЫ БЫТЬ
ВНИМАТЕЛЬНЫ.
При необходимости вместо единиц массы могут быть использованы единицы
веса. Затем с помощью оператора PARAM,WTMASS вес преобразуется в массу.
Преобразование “вес - масса”:
Масса = (1/G) · Вес (G = ускорение свободного падения)
Плотность = (1/G) · Удельный вес
Оператор PARAM,WTMASS, выполняет преобразование с коэффициентом = 1/G. По умолчанию коэффициент =1,0.
Пример:
При G = 386,4 in/sec2 надо задать PARAM, WTMASS, 0.00259
Оператором PARAM,WTMASS инициализируется однократное преобразование веса в массу (включая MASSi, CONMi и неконструкционные массы). Не используйте “смесь” массовых и весовых характеристик. Используйте либо массу, либо вес.
Слайд 14
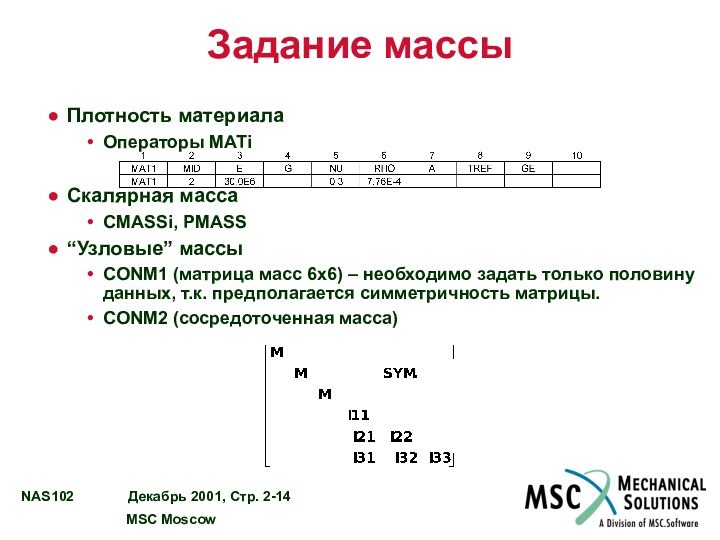
Задание массы
Плотность материала
Операторы MATi
Скалярная масса
CMASSi, PMASS
“Узловые” массы
CONM1 (матрица
масс 6x6) – необходимо задать только половину данных, т.к.
предполагается симметричность матрицы.
CONM2 (сосредоточенная масса)
Слайд 15
Задание массы
Неконструкционная масса
Задание характеристик массы в операторе свойств
элемента, которая не ассоциируется с его геометрическими параметрами: отношение
массы к длине для 1-D элементов и отношение массы к площади для 2-D элементов.
Слайд 18
Основные операции над наборами степеней свободы в MSC.Nastran
MSC.Nastran
Quick Reference Guide: