Слайд 2
Порядок выполнения работы
Вариант выбирается из папки Варианты для
контрольной и лабораторной. Данные варианта импортируются в MATLAB. Все
признаки должны быть числовыми или приводиться к таковым и быть нормализованными (находиться в [0,1]). Если признак нечисловой (категориальный, то есть принимает значение из нкоторого списка), то его надо привести к числовому.
Один признак является классификационным.
1. Разделить данные варианта на обучающую и тестирующую выборки (примерно поровну) так, чтобы в каждой выборке было примерно поровну экземпляров каждого класса. Для этого строки матрицы нужно предварительно отсортировать по значениям классификационного признака (команда sortrows)
2. По обучающей выборке построить классификационное дерево решений; имена признаков назначаются из описания предметной области варианта
3. Построить дерево минимальной стоимости
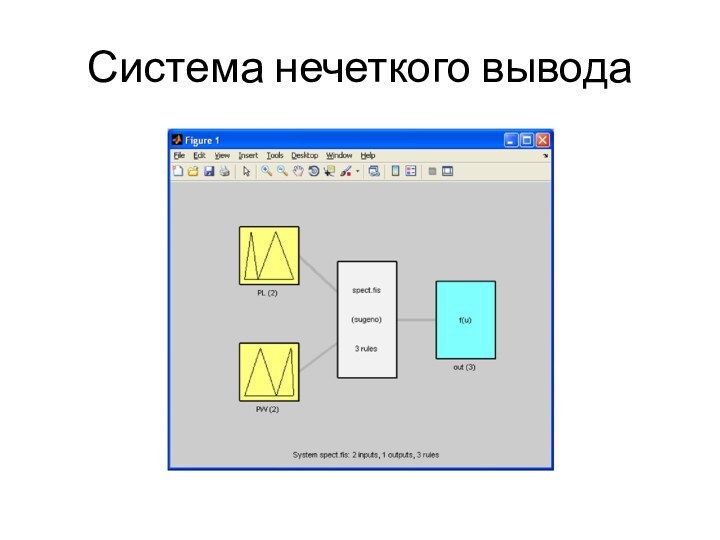
По дереву решений минимальной стоимости сформировать систему нечеткого вывода (fis)
типа Сугено с треугольными функциями принадлежности термов, входные переменные которой – дуги дерева решений, выходная переменная – номер или имя класса.
Сохранить fis в файле и выдать ее на экран
5.Отдельно данные обучающей выборки и тестирующие данные классифицировать с помощью дерева решений минимальной стоимости и с помощью системы нечеткого вывода.
6.Результаты разместить в таблице вида:сравниваются, и подсчитывается число совпадений по каждому классу отдельно по обучающей и по контролирующей выборке
Слайд 3
Деревья решений
Деревья решений – это способ представления правил
в иерархической, последовательной структуре, где каждому объекту соответствует единственный
узел, дающий решение.
Под правилом понимается логическая конструкция, представленная в виде "если ... то ...".
Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов.
Целевая переменная должна иметь дискретные значения.
Слайд 4
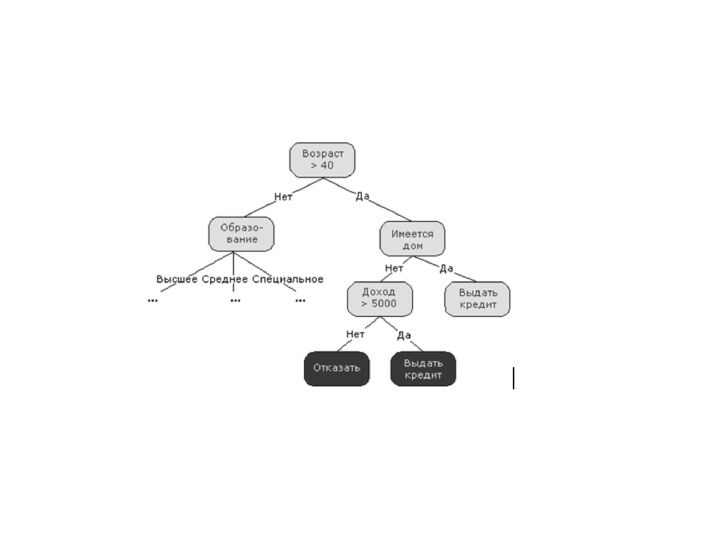
Как построить дерево решений?
Пусть нам задано некоторое обучающее

множество T, содержащее объекты (примеры), каждый из которых характеризуется
m признаками, причем один из них указывает на принадлежность объекта к определенному классу.
Пусть через {C1, C2, ... Ck} обозначены классы, тогда существуют 3 ситуации:
1. множество T содержит один или более примеров, относящихся к одному классу Ck. Тогда дерево решений для Т – это лист, определяющий класс Ck;
2. множество T не содержит ни одного примера, т.е. пустое множество. Тогда это снова лист, и класс, связанный с листом, выбирается из другого множества отличного от T, скажем, из множества, связанного с родителем;
3. множество T содержит примеры, относящиеся к разным классам. В этом случае следует разбить множество T на некоторые подмножества. Для этого выбирается один из признаков, имеющий два и более отличных друг от друга значений O1, O2, ... On. T разбивается на подмножества T1, T2, ... Tn, где каждое подмножество Ti содержит все примеры, имеющие значение Oi для выбранного признака. Это процедура будет рекурсивно продолжаться до тех пор, пока конечное множество не будет состоять из примеров, относящихся к одному и тому же классу.
Слайд 6
Вышеописанная процедура лежит в основе многих современных алгоритмов
построения деревьев решений, этот метод известен еще под названием
разделения и захвата (divide and conquer).
Очевидно, что при использовании данной методики построение дерева решений будет происходит сверху вниз.
Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning).
На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений, но наибольшее распространение и популярность получил следующий:
Слайд 7
CART (Classification and Regression Tree)
– это алгоритм
построения бинарного дерева решений – дихотомической классификационной модели.
Каждый
узел дерева при разбиении имеет только двух потомков
Слайд 8
Большинство из известных алгоритмов являются "жадными алгоритмами".
Если
один раз был выбран признак, и по нему было
произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой признак, который дал бы лучшее разбиение.
Поэтому на этапе построения нельзя сказать, даст ли выбранный признак, в конечном итоге, оптимальное разбиение.
Слайд 9
Этапы построения деревьев решений
При построении деревьев решений особое
внимание уделяется следующим вопросам:
выбору признака, по которому пойдет
разбиение
выбор критерия остановки обучения
Слайд 10
Правило разбиения
Каким образом следует выбрать признак?
Для построения дерева
на каждом внутреннем узле необходимо найти такое условие, которое
бы разбивало множество, связанное с этим узлом, на подмножества. В качестве такой проверки должен быть выбран один из признаков.
Общее правило для выбора признака можно сформулировать следующим образом: выбранный признак должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов ("примесей") в каждом из этих множеств было как можно меньше.
Слайд 11
Были разработаны различные критерии, один из них -
Статистический критерий
Алгоритм CART использует так называемый индекс Gini (в
честь итальянского экономиста Corrado Gini), который оценивает "расстояние" между распределениями классов.
где c – текущий узел, а pj – вероятность того, что узел c принадлежит классу j
Слайд 12
Функции Matlab для работы с деревьями решений
Расчет бинарного
дерева классификации наблюдений
T = treefit(X,y) функция предназначена для
расчета структуры Т, определяющей параметры бинарного дерева классификации наблюдений для матрицы независимых переменных Х и вектора значений зависимой переменной y. Размерность матрицы Х - n×m, где n - число наблюдений, m - количество независимых переменных. Строки Х соответствуют наблюдениям, столбцы Х - независимым переменным. Число элементов вектора y должно быть равно n. Вектор y задается как вектор строк
Выходная переменная T определяет бинарное дерево решений, в котором промежуточные узлы делятся ветвями на 2 возможных решения. В качестве условия выбора направления перехода выступает ограничение на значение независимой переменной.
Слайд 13
Графическое представление бинарного дерева классификации
treedisp(T) функция позволяет

получить графическое представление бинарного дерева для классификации наблюдений на
основе входного аргумента T. Параметр Т определяет вид дерева решений и задается как структура. Т является выходным аргументом функции treefit. Результат отображается в графическом окне. Промежуточные узлы дерева решений отмечены метками с условиями выбора относительно значения какой либо независимой переменной. Каждый из конечных узлов дерева решений имеет метку со значением зависимой переменной. Для выбора одной из двух возможных ветвей дерева решений исходящих из промежуточного узла действует правило: левая ветвь соответствует выполнению условия относительно независимой переменной, правая - невыполнению этого условия. Определение значения зависимой переменной начинается с первого промежуточного узла, далее, следуя заданному условию, выбирается правая или левая исходящая ветвь. Аналогично просматриваются последующие узлы до тех пор, пока не будет достигнут последний конечный узел. Символьная метка, соответствующая последнему узлу, является значением зависимой переменной.
Слайд 14
Пример использования
функции treefit
Задача классификации ирисов Фишера для
4 независимых переменных meas, заданных на числовой шкале, и
зависимой переменной species, элементы вектора которой заданы как 3 значения по категориальной шкале.
>> load fisheriris
>> t = treefit(meas,species);
>> treedisp(t,'names',{'SL' 'SW' 'PL' 'PW'});
Слайд 16
Расчет погрешности классификации на основе дерева решений
cost

= treetest(T,'resubstitution') функция позволяет рассчитать погрешность классификации, определяемой бинарным
деревом решений Т методом обратной подстановки исходных значений зависимой и независимых переменных. Входной аргумент Т формируется с помощью функции treefit. Вероятностью p(i) является отношение числа неверных классификаций по i-му значению зависимой переменной из начального множества данных к объему исходной выборки. Выходная переменная cost является вектором погрешностей для последовательности классификаций, полученных в процессе совращения уровней в исходном бинарном дереве решений Т. Поскольку расчет вектора ошибок основан на исходной выборке по которой была рассчитана структура Т, то элементы вектора cost будут представлять нижнюю границу доверительного интервала погрешности при использовании новой выборки.
cost = treetest(T,'test',X,y) функция предназначена для расчета вектора погрешностей cost классификации, определяемой структурой Т по тестовой выборке X, y. Х матица значений независимых переменных. Столбцы Х соответствуют независимым переменным, строки - наблюдениям. y - вектор значений зависимой переменой. Тестовая выборка и исходная выборка, использованная в treefit при расчете Т, должны быть различны. Количество и порядок независимых переменных, столбцов матриц Х в исходной и тестовой выборках, должно быть одинаковым.
[cost,secost,ntnodes,bestsize] = treetest(...) функция позволяет рассчитать:
1. cost - вектор погрешностей классификации;
2. secost - вектор стандартных ошибок для элементов вектора cost;
3. ntnodes - вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений;
4. bestsize - скаляр, определяющий оптимальный уровень сокращения полного дерева решений Т. Если bestsize=0, то оптимальным будет полное бинарное дерево решений Т. Величина bestsize должна соответствовать наименьшему бинарному дереву решений, обеспечивающему погрешность классификации, равной минимальной погрешности плюс ее стандартная ошибка.
Слайд 17
Расчет параметров сокращенного бинарного дерева решений
T2 =
treeprune(T1,'level',level) функция предназначена для получения сокращенного до уровня 'level'
дерева классификации T2 из начального бинарного дерева решений T1. T1 является выходной переменной функции treefit. Значение параметра 'level' - level должно быть целым положительным числом. Если level=0 то T2 будет получено без сокращения T1. Исходное бинарное дерево решений T1 сокращается по оптимальной схеме, т.е. в первую очередь удаляются промежуточные узлы, соответствующие наименьшему уменьшению погрешности дерева классификации.
Слайд 18
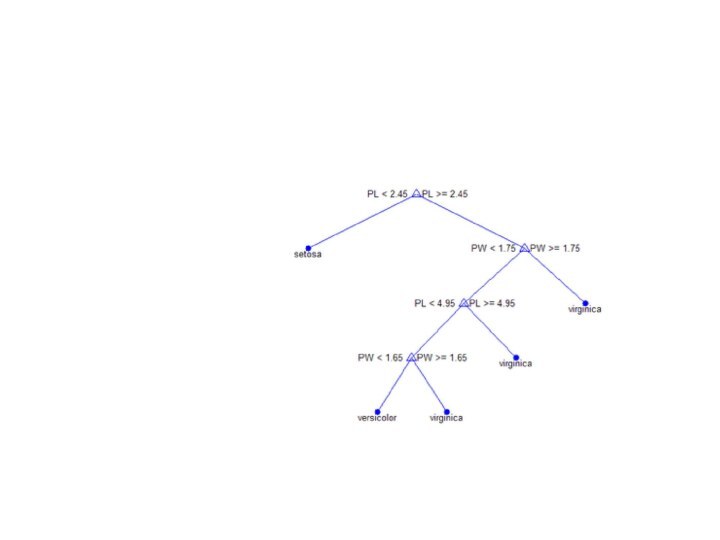
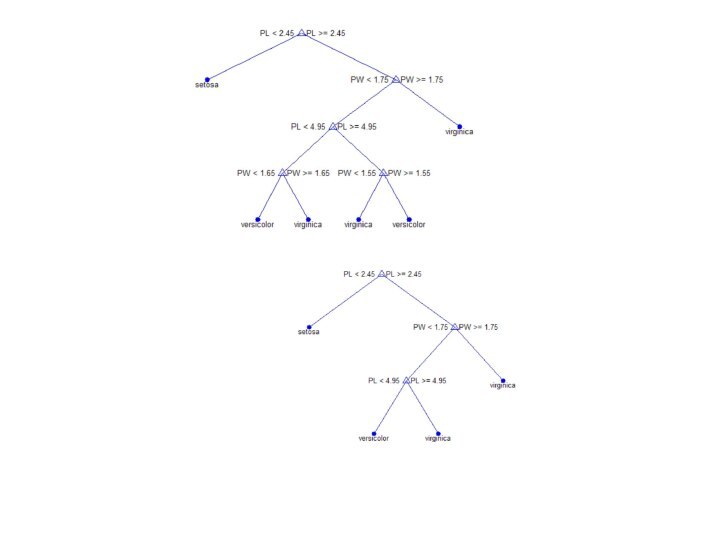
Пример
Отобразим полное дерево для ирисов Фишера и оптимальное
дерево минимальной стоимости
load fisheriris;
t1 = treefit(meas,species);
treedisp(t1,'names',{'SL' 'SW'
'PL' 'PW'});
[cost,secost,nt,best]=treetest(t,'cross',meas,species);
t2 = treeprune(t1,'level',best);
treedisp(t2,'names',{'SL' 'SW' 'PL' 'PW'});
Слайд 20
Расчет классификационного признака по дереву
YFIT = treeval(T,X) функция

позволяет определить значения классификационного признака YFIT по дереву, параметры
которого задаются структурой T, для значений независимых переменных Х. Структура Т формируется как выходной аргумент функции treefit. Х задается как матрица с размерностью n×m, где n - число наблюдений, m - количество независимых переменных. Строки Х соответствуют наблюдениям, столбцы Х - независимым переменным. Выходная переменная YFIT является вектором значений с числом элементов равным n. Значение YFIT(j) рассчитывается согласно строкам X(j,:).
YFIT(j) является номером класса, которому принадлежит точка с координатами X(j,:) в пространстве независимых переменных. Для определения названия класса соответствующего номеру YFIT(j) используется третий выходной аргумент cname
[YFIT,NODE] = treeval(...) кроме значений классификационного признака функция возвращает массив номеров узлов NODE, соотнесенных c каждой строкой матрицы независимых переменных Х(j,:). Размерность YFIT и NODE будет совпадать.
[YFIT,NODE,CNAME] = treeval(...) функция возвращает массив ячеек CNAME, содержащий названия классов найденных по дереву решений Т.
Слайд 21
Пример
load fisheriris;
t = treefit(meas,species);
[cost,secost,ntnodes,bestsize] = treetest(t,'cross',meas,species);
t2 = treeprune(t,'level',bestsize);
treedisp(t2,'names',{'SL' 'SW' 'PL' 'PW'});
[sfit2,A,CNAME2]
= treeval(t2,meas);
mean(strcmp(CNAME2,species))
% Доля правильно классифицированных объектов
Слайд 22
Нечеткое множество
В основе этого понятия лежит представление

о том, что составляющие данное множество элементы, обладающие общим
свойством, могут обладать этим свойством в различной степени, то есть степень принадлежности к множеству может быть различной. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.
Нечетким множеством (fuzzy set) A на универсальном множестве U называется совокупность пар
,где - степень принадлежности элемента uϾ U к нечеткому множеству . Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.
Функцией принадлежности (membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.
Пример 1. Представить в виде нечеткого множества понятие “мужчина среднего роста”.
Решение: A={ 0/155+0.1/160 + 0.3/165 + 0.8/170 +1/175 +1/180 + 0.5/185 +0/180.}
Лингвистической переменной (linguistic variable) называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.
Терм–множеством (term set) называется множество всех возможных значений лингвистической переменной.
Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.
Слайд 23
Нечеткая база знаний
Нечеткой базой знаний называется совокупность нечетких
правил
"Если - то",
определяющих взаимосвязь между входами и
выходами исследуемого объекта. Обобщенный формат нечетких правил такой:
Если посылка правила, то заключение правила.
Посылка правила представляет собой утверждение типа "x есть низкий", где "низкий" - это терм, заданный нечетким множеством на универсальном множестве лингвистической переменной x. Квантификаторы "очень", "более-менее", "не", "почти" и т.п. могут использоваться для модификации термов антецедента.
Заключение правила представляет собой утверждение типа "y есть d", в котором значение выходной переменной (d) может задаваться:
нечетким термом: "y есть высокий";
классом решений: "y есть бронхит"
четкой константой: "y=5";
четкой функцией от входных переменных: "y=5+4*x".
Слайд 24
Пример 2. Рассмотрим переменную “скорость автомобиля”, которая оценивается
по шкале “низкая", "средняя", "высокая” и “очень высокая".
В этом
примере лингвистической переменной является “скорость автомобиля”, термами - лингвистические оценки “низкая", "средняя", "высокая” и “очень высокая”, которые и составляют терм–множество.
Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число.
Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox MATLAB запрограммированы такие методы дефаззификации:
Centroid - центр тяжести;
Bisector - медиана;
LOM (Largest Of Maximums) - наибольший из максимумов;
SOM (Smallest Of Maximums) - наименьший из максимумов;
Mom (Mean Of Maximums) - центр максимумов.
Слайд 25
Пример. Следующая нечеткая база знаний описывает зависимость между
возрастом водителя (x) и возможностью дорожно-транспортного происшествия (y):
Если x
= Молодой, то y = Высокая;
Если x = Средний, то y = Низкая;
Если x = Очень старый, то y = Высокая.
Слайд 26
Нечеткий логический вывод
Обычный, булев логический вывод базируется на
правиле модус поненс, которое можно записать так:
Посылка A есть
истинно
Импликация Если A, то B
Логический вывод B есть истинно
Модус поненс выводит заключение "B есть истинно", если известно, что "A есть истинно" и существует правило "Если A, то B" (A и B - четкие логические утверждения). Однако, если прецедент отсутствует, то модус поненс не сможет вывести никакого, даже приближенного заключения. Даже в случае, когда известно, что близкое к A утверждение A' является истинным, модус поненс не может быть применен. Одним из возможных способов принятия решений при неопределенной информации является применение нечеткого логического вывода.
Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с использованием нечеткой базы знаний и нечетких операций.
Слайд 27
Алгоритм Мамдани
Формирование базы правил систем нечеткого вывода.
Фаззификация
входных переменных.
Агрегирование подусловий в нечетких правилах продукций. Для
нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.
Активизация подзаключений в нечетких правилах продукций.
Аккумуляция заключений нечетких правил продукций.
Дефаззификация выходных переменных.
Слайд 28
Алгоритм Сугено
Формирование базы правил систем нечеткого вывода.
В
базе правил используются только правила нечетких продукций в форме:
ПРАВИЛО
<#>: ЕСЛИ "β1 есть α’" И " β2 есть α’’" ТО "w=ε1∙a1+ε2∙a2".
Здесь ε1, ε2 —некоторые весовые коэффициенты. При этом значение выходной переменной w в заключении определяется как некоторое действительное число.
Фаззификация входных переменных.
Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min-конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.
Слайд 29
Активизация подзаключений в нечетких правилах продукций. Во-первых, с
использованием метода (8.6) находятся значения степеней истинности всех заключений
правил нечетких продукций. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила. Это выполняется с использованием формулы для заключения (8.16), в которую вместо а1 и а2 подставляются значения входных переменных до этапа фаззификации. Тем самым определяются множество значений С={с1, с2,..., сn} и множество значений выходных переменных W={w1, w2,..., wn}, где п — общее количество правил в базе правил.
Аккумуляция заключений нечетких правил продукций. Фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами wj
Дефаззификация выходных переменных. Используется модифицированный вариант в форме метода центра тяжести
Слайд 30
Функции matlab для работы с fis
EVALFIS
Выполнение нечеткого логического
вывода
output = evalfis(input, fis)
Выполняет нечеткий логический вывод. Функция evalfis
может иметь два входных аргумента:
input – матрица значений входных переменных, для которых необходимо выполнить нечеткий логический вывод. Матрица должна иметь размер M x N, где N – количество входных переменных; M – количество входных данных. Каждая строчка матрицы представляет один вектор значений входных переменных;
fis – идентификатор системы нечеткого логического вывода;
Функция evalfis может иметь один выходной аргумента:
output – матрица значений выходных переменных, получаемая в результате нечеткого логического вывода для вектора входных значений input. Матрица имеет размер M x L, где M – количество входных данных; L – количество выходных переменных в fis;
Слайд 31
Создание новой системы нечеткого логического вывода
fis = newfis(fis_name,
fis_type)
Создает в рабочей области новую систему нечеткого логического вывода.
Входные аргументы:
fis_name - наименование системы нечеткого логического вывода;
fis_type - тип системы нечеткого логического вывода. Допустимые значения:'mamdani' - система типа Мамдани (значение по умолчанию);'Sugeno' - система типа Сугэно;
Пример:
a=newfis('new_fuzzy_system')
В рабочей области создается структура a, содержащая систему нечеткого логического вывода с именем 'new_fuzzy_system'. Значения всех параметров системы устанавливаются по умолчанию.
Слайд 32
addvar Добавляет переменную в систему нечеткого логического вывода
FIS_name=

addvar (FIS_name, varType, varName, varBound)
Переменную можно добавить только к
существующей в рабочей области MatLab системе нечеткого логического вывода. Функция addrvar имеет четыре входных аргумента:
FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
varType – тип добавляемой переменной. Допустимые значения - ‘input’ - входная переменная и ‘output’ – выходная переменная;
varName – наименование добавляемой переменной. Задается в виде строки символов;
varBound – вектор, задающий диапазон изменения добавляемой переменной.
Порядковый номер переменной в системе нечеткого логического вывода соответствует порядку добавления с помощью функции addvar, т.е. первая добавленная переменная будет иметь порядковый номер 1. Входные и выходные переменные нумеруются независимо.
Пример.
FIS_name=addvar(FIS_name, ‘input’, ‘Рост’, [155 205])
Строка добавляет в систему нечеткого логического вывода FIS_name входную переменную ‘Рост’, заданную на интервале [155 205].
Слайд 33
addmf Добавляет функцию принадлежности к системе нечеткого логического

вывода
FIS_name=addmf(FIS_name, varType, varIndex, mfName, mfType, mfParams)
Функцию принадлежности можно добавить
только к существующей в рабочей области MatLab системе нечеткого логического вывода. Другими словами, система нечеткого логического вывода должна быть каким-то образом загружена в рабочую область или создана с помощью функции newfis. Функция addmf имеет шесть входных аргументов:
FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
varType – тип переменной, к которой добавляется функция принадлежности. Допустимые значения - ‘input’ - входная переменная и ‘output’ – выходная переменная;
varIndex – порядковый номер переменной, к которой добавляется функция принадлежности;
mfName – наименование добавляемой функции принадлежности (терм). Задается в виде строки символов;
mfType – тип (модель) добавляемой функции принадлежности. Задается в виде строки символов;
mfParams – вектор параметров добавляемой функции принадлежности.
Порядковый номер функции принадлежности в системе нечеткого логического вывода соответствует порядку добавления с помощью функции addmf, т.е. первая добавленная функция принадлежности всегда будет иметь порядковый номер 1. С помощью функции addmf невозможно добавить функцию принадлежности к несуществующей переменной. В этом случае необходимо вначале добавить переменную к системе нечеткого логического вывода с помощью функции addvar.
Пример.
FIS_name=addmf(FIS_name, ‘input’, 1, ‘низкий’, ‘trapmf’, [150, 155, 165, 170])
Строка добавляет в терм-множество первой входной переменной нечеткой системы FIS_name терм ‘низкий’ с трапециевидной функцией принадлежности с параметрами [150, 155, 165, 170].
Слайд 34
Добавление правил в базу знаний fis
FIS_name= addrule (FIS_name,
ruleList)
Правила можно добавить только к существующей в рабочей области
MatLab системе нечеткого логического вывода. Функция addrule имеет два входных аргумента:
FIS_name – идентификатор системы нечеткого логического вывода в рабочей области MatLab;
ruleList – матрица добавляемых правил.
Матрица правил должна быть задана в формате indexed. Количество строк матрицы ruleList равно количеству добавляемых правил, т.е. каждая строка матрицы соответствует одному правилу. Количество столбцов матрицы равно m+n+2, где m (n) – количество входных (выходных) переменных системы нечеткого логического вывода.
Первые m столбцов соответствуют входным переменным, т.е. задают ЕСЛИ-часть правил. Элементы этих столбцов содержат порядковые номера термов, используемых для лингвистической оценки соответствующих входных переменных. Значение 0 указывает, что соответствующая переменная в правиле не задана, т.е. ее значение равно none.
Слайд 35
Следующие n столбцов соответствуют выходным переменным, т.е. задают
ТО-часть правил. Элементы этих столбцов содержат порядковые номера термов,
используемых для лингвистической оценки соответствующих выходных переменных.
Предпоследний столбец матрицы содержит весовые коэффициенты правил. Значения весовых коэффициентов должны быть в диапазоне [0, 1].
Последний столбец матрицы задает логические связки между переменными внутри правил. Значение 1 соответствует логической операции И, а значение 2 – логической операции ИЛИ.
Пример.
FIS_name=addrule(FIS_name, [1 1 1 1 1; 1 2 2 0.5 1])
Строка добавляет в базу знаний системы FIS_name два правила, которые интерпретируются следующим образом:
Если вход1=MF1 и вход2=MF1, то выход1=MF1 с весом 1,
Если вход1=MF1 и вход2=MF2, то выход1=MF2 с весом 0.5,
где MF1 (MF2) – терм с порядковым номером 1 (2).
Слайд 36
Замена правил FIS
outfis = parsrule (infis, inrulelist, ruleformat,

lang)
[outfis, outrulelist, errorstr] = parsrule (infis, inrulelist, ruleformat, lang)
Функция
parsrule предназначена для ввода правил в нечеткую базу знаний. При этом удаляются ранее существующие в базе знаний правила. Функция parsrule может иметь до четырех входных аргументов, первые два из которых обязательные:
infis - идентификатор исходной системы нечеткого логического вывода;
inrulelist - список правил "если - то". Правила можно задавать в виде предложений на английском языке При задании правил на естественном языке необходимо использовать следующие ключевые слова:
для английского языка - "if", "and", "or", "then", "is", "not";
которые эквиваленты русским словам "если", "и", "или", "то", "есть", "не", соответственно. Весовой коэффициент можно указать в конце правила. По умолчанию значение весового коэффициента равно 1. Список правил задается в виде матрицы, каждая строчка которой определяет одно правило;
Функция parsrule может иметь до трех выходных аргументов:
outfis - идентификатор системы нечеткого логического вывода с новыми правилами;
outrulelist - список правил системы outfis. Список представляет собой матрицу целых положительных чисел, соответствующих правилам, заданных матрицей inrulelist. Для преобразование чисел в символы необходимо использовать функцию char. Вошедшие в outfis корректно заданные правила в этом списке имеют порядковый номер. Наличие символа '#' указывает на то, что соответствующее правило является некорректным.
errorstr - список ошибок задания правил.
Слайд 37
Пример
infis=readfis('tipper');
r1='if service is good then tip is average
';
r2='if service is poor and food is rancid then
tip is cheap ';
r3='if service is excellent and food is delicious then tip is generous';
inrulelist=[r1; r2; r3];
outfis=parsrule(infis,inrulelist)
Загружается в рабочую область демонстрационная система нечеткого логического вывода "Tipper", задающая зависимость размера чаевых от качества пищи и уровня сервиса в ресторане. Затем формируется новая база знаний, содержащая следующие правила:
"if service is good then tip is average";
"if service is poor and food is rancid then tip is cheap";
"if service is excellent and food is delicious then tip is generous'".
Слайд 38
Запись FIS в файл
writefis (fis, filename, 'dialog')
Функция writefis

сохраняет систему нечеткого логического вывода на диске. Функция writefis
может иметь до трех входных аргументов:
fis – обязательный аргумент, задающий систему нечеткого логического вывода;
filename – имя файла, в котором будет сохранена система нечеткого логического вывода;
'dialog' – константа, вызывающая типовое диалоговое окно записи файла на диск. В этом окне в качестве имени файла используется значение аргумента filename. Пользователь может изменить имя файла а также указать папку, в которую будет производиться запись.
При вызове функции writefis с одним аргументом будет открыто типовое диалоговое окно записи файла на диск. Однако, в отличие от вызова функции с тремя аргументами, имя файла по умолчанию в этом окне установлено не будет.
При вызове функции writefis с двумя аргументами диалоговое окно записи файла на диск не появится. Система будет сохранена в текущей папке. Расширение “.fis” будет добавлено к имени файла в случае, если это расширение не было задано аргументом filename.
Пример:
fis = readfis (‘tipper’);
writefis (fis, ‘tipper_copy’)
Запись демонстрационной системы нечеткого логического вывода “Tipper” в файл с именем “tipper_copy.fis”.
Слайд 39
Пример совместного использования дерева решений и нечеткого вывода
В
качестве примера возьмем выборку ирисов Фишера, в которой хранится
150 объектов, имеющих по 4 признака и принадлежащих к 3 сортам (setoza, versicolor,virginica)
load fisheriris %Çàãðóçêà ôàéëà
P_train1=meas(1:25,:);%Ôîðìèðîâàíèå îáó÷àþùåé
P_train2=meas(51:75,:);% ïîñëåäîâàòåëüíîñòè
P_train3=meas(101:125,:);
P_train=[P_train1;P_train2;P_train3];
T_train(1:25,1)=species(1:25,1);%Ôîðìèðîâàíèå ãðóïïèðîâî÷íûõ äàííûõ
T_train(26:50,1)=species(51:75,1);%äëÿ îáó÷àþùåé ïîñëåäîâàòåëüíîñòè
T_train(51:75,1)=species(101:125,1);
t = treefit(P_train,T_train%Построение дерева
[c,s,n,best] = treetest(t,'cross',P_train,T_train,'treesize','se');
tmin=treeprune(t,’level’,best);
%Построение дерева минимальной стоимости
treedisp(tmin,'names',{'SL' 'SW' 'PL' 'PW'});
% Вывод дерева минимальной стоимости
[sfit2,A,CNAME_train_tree] = treeval(tmin,P_train);
% Доля правильно классифицированных объектов обучающей выборки
Слайд 40
%Ôîðìèðîâàíèå êîíòðîëèðóþùåéâûáîðêè
P_ch1=meas(26:50,:);
P_ch2=meas(76:100,:);
P_ch3=meas(126:150,:);
P_ch=[P_ch1;P_ch2;P_ch3];
%Âû÷èñëåíèå çíà÷åíèé ãðóïïèðîâî÷íîãî ïðèçíàêà
%äëÿ êîíòðîëèðóþùåé
âûáîðêè
T_ch(1:25,1)=species(26:50,1);
T_ch(26:50,1)=species(76:100,1);
T_ch(51:75,1)=species(126:150,1);
[sfit2,A,CNAME_ch_tree] = treeval(tmin,P_ch);
% Äîëÿ ïðàâèëüíî êëàññèôèöèðîâàííûõ îáúåêòîâ êîíòðîëèðóþùåé
âûáîðêè âûáîðêè
er_tree_ch=mean(strcmp(CNAME_ch_tree,T_ch));
Слайд 41
fis = newfis('spect.fis','sugeno');
%Создание системы нечеткого вывода
fis = addvar(fis,

'input', 'PL', [1 6.9]);
%Добавление входных и выходных переменных, их
термов и правил
fis = addmf(fis,'input',1,'low','trimf',[1 1.8 2.6]);
fis = addmf(fis,'input',1,'high','trimf',[2.6 4.75 6.9]);
fis = addvar(fis, 'input', 'PW', [0.1 2.5]);
fis = addmf(fis,'input',2,'low','trimf',[0.1 0.87 1.65]);
fis = addmf(fis,'input',2,'high','trimf',[1.65 2.37 2.5]);
fis = addvar(fis, 'output', 'out', [ 1 3]);
fis = addmf(fis,'output',1,'setosa','constant',1);
fis = addmf(fis,'output',1,'versicolor','constant',2);
fis = addmf(fis,'output',1,'virginica','constant',3);
ruleList=[
1 0 1 1 1;
2 1 2 1 1;
2 2 3 1 1;
];
%Альтернативн о
r1='if PL is low then out is setosa ';
r2='if PL is high and PW is low then out is versicolor ';
r3='if PL is high and PW is high then out is virginica ';
inrulelist=[r1; r2; r3];
[fis, outrulelist, errorstr]=parsrule(fis,inrulelist);
%fis = addrule(fis, ruleList);
%Вывод системы нечеткого вывода
plotfis(fis);
writefis(fis,'spect.fis');
%Запись с%Формирование признаков, участвующих в системе нечеткого вывода
P_train34=P_train(:,3:4);
P_ch34=P_ch(:,3:4);
%Вычисление выходной величины по системе нечеткого вывода
Y_train=fix(evalfis(P_train34,fis));
Y_ch=fix(evalfis(P_ch34,fis));
Слайд 42
for i=1:75
if (Y_train(i,1)==1)
CNAME_train_fis{i,1}='setosa';
else
if (Y_train(i,1)==2)
CNAME_train_fis{i,1}='versicolor';
else
if (Y_train(i,1)==3)
CNAME_train_fis{i,1}='virginica';
end
end
end
end
Слайд 43
for i=1:75
if (Y_ch(i,1)==1)
CNAME_ch_fis{i,1}='setosa';
else
if (Y_ch(i,1)==2)
CNAME_ch_fis{i,1}='versicolor';
else
if (Y_ch(i,1)==3)
CNAME_ch_fis{i,1}='virginica';
end
end
end
end
er_fis_train=mean(strcmp(CNAME_train_fis,T_train));
er_fis_ch=mean(strcmp(CNAME_ch_fis,T_ch));

















![Нечеткий вывод и деревья решений Примерload fisheriris; t = treefit(meas,species); [cost,secost,ntnodes,bestsize] = treetest(t,'cross',meas,species); t2 = treeprune(t,'level',bestsize);](/img/tmb/15/1418522/735b7c915fdfed04fe3c478719110363-720x.jpg)














![Нечеткий вывод и деревья решений Замена правил FIS outfis = parsrule (infis, inrulelist, ruleformat, lang)[outfis, outrulelist, errorstr]](/img/tmb/15/1418522/18fcf4767c09dc11de6b4bde0fa4b6ea-720x.jpg)



![Нечеткий вывод и деревья решений %Ôîðìèðîâàíèå êîíòðîëèðóþùåéâûáîðêèP_ch1=meas(26:50,:); P_ch2=meas(76:100,:);P_ch3=meas(126:150,:);P_ch=[P_ch1;P_ch2;P_ch3];%Âû÷èñëåíèå çíà÷åíèé ãðóïïèðîâî÷íîãî ïðèçíàêà %äëÿ êîíòðîëèðóþùåé âûáîðêèT_ch(1:25,1)=species(26:50,1);T_ch(26:50,1)=species(76:100,1);T_ch(51:75,1)=species(126:150,1);[sfit2,A,CNAME_ch_tree] = treeval(tmin,P_ch); %](/img/tmb/15/1418522/cae1589faf2bb32a716a6591faca5464-720x.jpg)
![Нечеткий вывод и деревья решений fis = newfis('spect.fis','sugeno');%Создание системы нечеткого выводаfis = addvar(fis, 'input', 'PL', [1 6.9]);%Добавление](/img/tmb/15/1418522/cb07a106fbd9fc0f188a2d702d7fe98d-720x.jpg)