- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Інформаційна система дослідників керованості поширенням розрядів і імпульсів в неоднорідному електричному полі, зарядженому газі
Содержание
- 2. Модель
- 3. Завдання програмиТреба змоделювати поширення стримера. Вихідними даними будуть чотири тривимірних масива: Ne, Np, Nn,V 3
- 4. Алгоритм програмиАлгоритм програми можливо розбити на 5 кроків4
- 5. Крок 1Треба заповнити перший рівень сітки, при K=05
- 6. Крок 2На другому кроці потрібно заповнити граничні точки в масиві V (які задані явно)6
- 7. Крок 3Заповнюємо центральні точки масивів Ne, Np,
- 8. Крок 4Треба заповнити масив V, використовуючи пятиточкову схему.8
- 9. Крок 4При цьому ми отримуємо систему лінійних
- 10. Крок 5На кожному рівні, як було написано
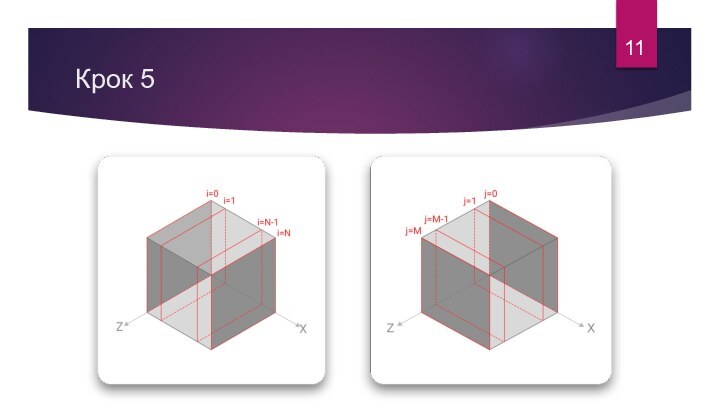
- 11. Крок 511
- 12. Результати12Наведені результати моделювання, отримані за рахунок інтегрування системи рівнянь, описаної в моделі
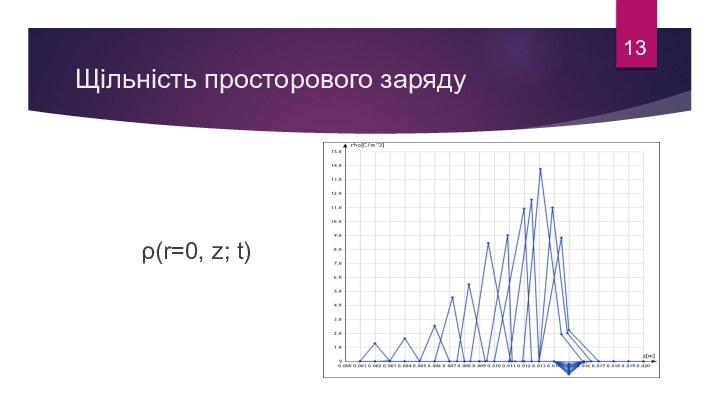
- 13. Щільність просторового заряду13ρ(r=0, z; t)
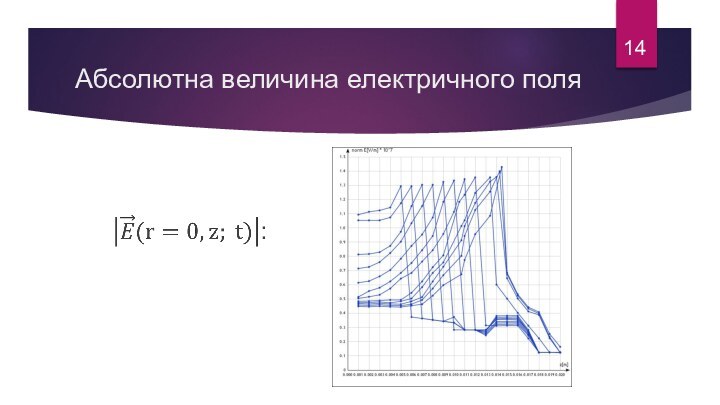
- 14. Абсолютна величина електричного поля14
- 15. Висновок15Мета роботи була досягнута, а саме: розроблена
- 16. Скачать презентацию
- 17. Похожие презентации
Модель
Слайд 3
Завдання програми
Треба змоделювати поширення стримера. Вихідними даними будуть
чотири тривимірних масива:
Слайд 7
Крок 3
Заповнюємо центральні точки масивів Ne, Np, Nn
на усіх рівнях, з k = 1 до k
= t. Центральними є точки які знаходяться в діапазоні від i = 1 до i = N по осі Х та від j = 1 до j = M по осі Z7
Слайд 9
Крок 4
При цьому ми отримуємо систему лінійних неоднорідних
рівнянь з (M - 1) * (N - 1)
невідомих для елементів матриці VДля розв’язання цієї системи ми скористалися формулою
(х = А-1 * F), де F - це вектор правих частин рівняння Пуасона.
9
Слайд 10
Крок 5
На кожному рівні, як було написано вище,
необхідно розставити границу по осі X (змінюється параметр i),
так як на границах вказані тільки похідні, а також заповнити значення в граничних точках по осі Z (змінюється параметр j)10
Слайд 12
Результати
12
Наведені результати моделювання, отримані за рахунок інтегрування системи
рівнянь, описаної в моделі
Слайд 15
Висновок
15
Мета роботи була досягнута, а саме: розроблена інформаційна
