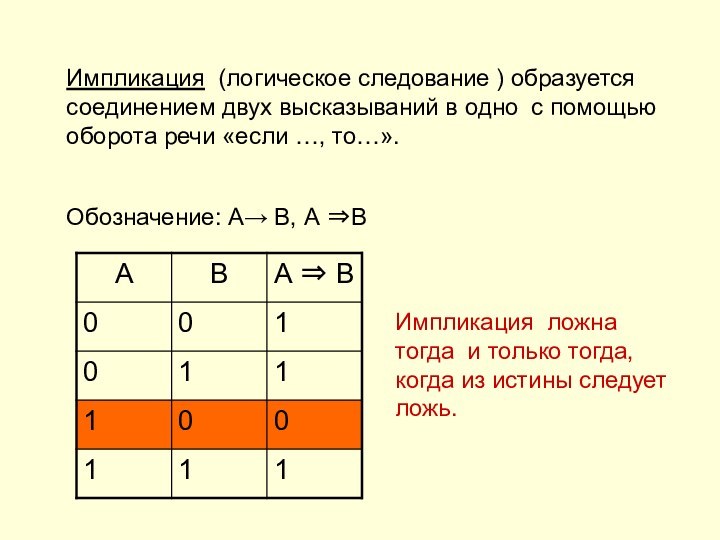
в одно с помощью оборота речи «если …, то…».
Обозначение:
А В, А ВИмпликация ложна тогда и только тогда, когда из истины следует ложь.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



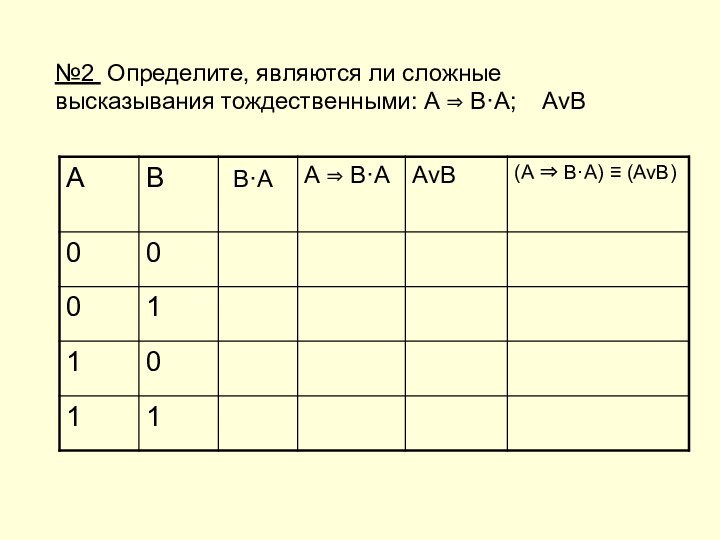


Импликация ложна тогда и только тогда, когда из истины следует ложь.
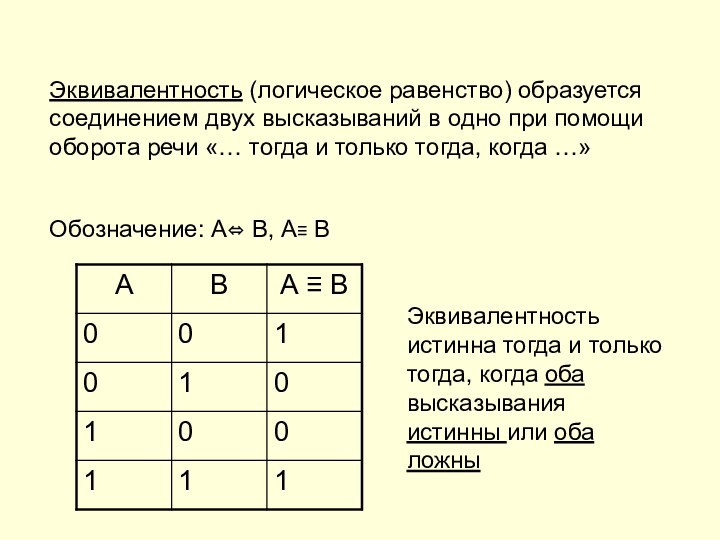
Эквивалентность истинна тогда и только тогда, когда оба высказывания истинны или оба ложны