- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятие информация
Содержание
- 2. Под информацией в быту понимают любые сведения
- 3. Под информацией в технике понимают любые сообщения,
- 4. Под информацией в теории управления (менеджменте) понимают
- 5. ключевые атрибуты информации. 1. Достоверность. информация
- 6. в узком смысле информацией можно назвать сведения
- 7. информацию можно подразделить на:1) структурную (или связанную)
- 8. Данные, знанияСведения, полученные путем измерения, наблюдения, логических
- 9. Свойства знаний1. Внутренняя интерпретируемость знаний (понятность знания
- 10. Введение информации в научно-технический и хозяйственный оборот
- 11. Пример 1. Как определить, какая из двух
- 12. Понятие битабит – это и двоичный знак,
- 13. Пример 2. А если монет 8? Тогда
- 14. Пример 3. Перейдем от монет к картам.
- 15. В этих примерах процесс получения информации рассматривается
- 16. Справедливо утверждение Хартли: если во множестве X={x1,x2,…,xn}
- 17. Вероятности отдельных букв в русском языке (с учетом пробела)
- 18. Частоты букв (в процентах) ряда европейских языков
- 19. Для неравновероятных процессов американский учёный Клод Шеннон
- 20. Можно представить что для того, чтобы получить
- 21. Из формулы непосредственно вытекают свойства энтропии:энтропия заранее
- 22. Кодирование источника сообщений Как уже отмечалось, результат
- 23. Если количество символов представляет собой степень двойки
- 24. Кодирование словами постоянной длины ld(7)≈2,807 и L=3..
- 25. В общем случае алгоритм построения оптимального кода
- 26. EABFC10101010111001001000EABFC100010101101000100011
- 27. При неравномерном кодировании вводят среднюю длину кодировки,
- 28. Средняя длина слова: L = 0,7+0,4+0,2=1,3.Среднее количество
- 29. Кодирование парСредняя длина кода одного знака равна
- 30. Скачать презентацию
- 31. Похожие презентации























Слайд 3
Под информацией в технике понимают любые сообщения, которые
зафиксированы в виде знаков и могут передаваться в виде
сигналов.Слайд 4 Под информацией в теории управления (менеджменте) понимают сообщения,
уменьшающие существующую до этого неопределенность в той предметной области,
к которой они относятся, и использующиеся для совершения активного действия, например, управленческого решения.Под информацией в теории управления (менеджменте) понимают сообщения, уменьшающие существующую до этого неопределенность в той предметной области, к которой они относятся, и использующиеся для совершения активного действия, например, управленческого решения.
Слайд 5
ключевые атрибуты информации.
1. Достоверность. информация свободна от
ошибок, чьей-либо пристрастности и отражает истинное положение дел. Часто
организации применяют независимые источники информации, чтобы анализируя их, уменьшать фактор пристрастности в принимаемом решении или в распространяемой производной информации.2. Оперативность. Доставка информации получателям в рамках необходимых временных границ. Например, вчерашняя газета сегодня, запоздавшая котировка акций. Своевременность просто означает, что адресат должен получить информацию, когда ему нужно.
3. Актуальность, т.е. важность, существенность для настоящего времени. Точная и своевременная информация может в то же время быть неактуальной, более того информация, актуальная для одного получателя, не обязательно актуальна для другого.
4. Полнота. Информация должна содержать все важные данные, которые ожидают от нее пользователи, и ее должно быть достаточно для понимания и принятия решения.
5. Полезность. Полезность (ценность) информации определяется по тем задачам, которые можно решить с ее помощью.
6. Понятность означает, что информация может быть представлена в ясном и понятном для потребителя формате. Потребитель информации – лицо, принимающее решение, должен как можно меньше времени тратить на дополнительные уточнения поступившей информации.
Слайд 6
в узком смысле информацией можно назвать сведения о
предметах, фактах, понятиях некоторой предметной области.
С середины XX века
информация рассматривается в широком смысле как общенаучное понятие, включающее в себя как совокупность сведений об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, так и обмен сведениями между людьми, человеком и автоматом, автоматом и автоматом, обмен сигналами между живой и неживой природой, в животном и растительном мире, а также генетическую информацию.
Слайд 7
информацию можно подразделить на:
1) структурную (или связанную) присущую
объектам неживой и живой природы естественного или искусственного происхождения.
Эти объекты (орудия труда, предметы быта, произведения искусства, научные теории и т.п.) возникают путем опредмечивания циркулирующей информации, то есть благодаря и в результате целенаправленных управленческих процессов;2) оперативную (или рабочую), циркулирующую между объектами материального мира и используемую в процессах управления в живой природе, в человеческом обществе
Слайд 8
Данные, знания
Сведения, полученные путем измерения, наблюдения, логических или
арифметических операций, и представленные в форме, пригодной для постоянного
хранения, передачи и обработки получили название данные.Совокупность полезной информации, правил и процедур ее обработки, необходимая для получения новой информации о какой-либо предметной области называют знанием.
Слайд 9
Свойства знаний
1. Внутренняя интерпретируемость знаний (понятность знания его
носителю).
2. Структурированность знаний. Информационные единицы должны обладать гибкой структурой.
Принцип «матрешки» – рекурсивная вложимость знаний. Возможность произвольного установления и перенастройки отношений (включения) между информационными единицами.3. Связность. Отношения между элементами: структурные, функциональные, казуальные и семантические. Структурные задают иерархию, функциональные задают процедурную информацию, позволяющие находить одни элементы через другие, каузальные задают причинно-следственные связи, семантические охватывают все остальные виды отношений.
4. Ассоциативность знаний – наличие семантической метрики в сфере знаний. Отношение релевантности на множестве информационных единиц характеризует ситуационную близость элементов (силу ассоциативной связи). Позволяет находить знания, близкие к уже
найденным.
5. Активность знаний – наличие у знаний побуждающей и направляющей функции, что фактически превращает знания в квазипотребности. Актуализации тех или иных действий способствуют имеющиеся в системе знания.
Слайд 10 Введение информации в научно-технический и хозяйственный оборот привело
к необходимости ее количественной оценки, т.е. к введению меры
сравнения. В простейшей комбинаторной форме эта мера была предложена Р. Хартли в 1928 году.Слайд 11 Пример 1. Как определить, какая из двух монет
фальшивая, если на вид они одинаковы, но известно, что
фальшивая легче. Нет ничего проще, скажете вы. Проводим одно взвешивание на чашечных весах, и все становится ясно. Таким образом, до взвешивания у вас была неопределенность по поводу того, какая из монет фальшивая, а после взвешивания вы сняли эту неопределенность, получив информацию. Иными словами, вы получили сообщение в элементарном альтернативном выборе между двумя событиями («фальшивая – не фальшивая», «да - нет», «истина – ложь», «0–1»).
Слайд 12
Понятие бита
бит – это и двоичный знак, и
единица измерения количества информации, определяемая как количество информации в
выборе с двумя взаимоисключающими равновероятными исходами.Слайд 13 Пример 2. А если монет 8? Тогда делим
их на две равные части и взвешиваем их. Ту
часть, которая легче, снова делим на две части и снова взвешиваем и т.д. За три взвешивания мы определим фальшивую монету.За три выбора мы уменьшили существующую неопределенность в 2, 4, 8 раз, получив таким образом 3 бита информации.
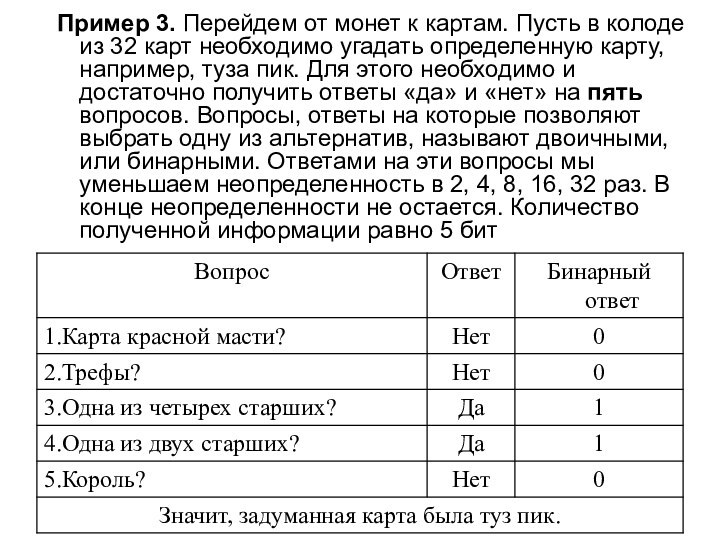
Слайд 14 Пример 3. Перейдем от монет к картам. Пусть
в колоде из 32 карт необходимо угадать определенную карту,
например, туза пик. Для этого необходимо и достаточно получить ответы «да» и «нет» на пять вопросов. Вопросы, ответы на которые позволяют выбрать одну из альтернатив, называют двоичными, или бинарными. Ответами на эти вопросы мы уменьшаем неопределенность в 2, 4, 8, 16, 32 раз. В конце неопределенности не остается. Количество полученной информации равно 5 битСлайд 15 В этих примерах процесс получения информации рассматривается как
выбор одного сообщения из конечного наперёд заданного множества из
n равновероятных сообщений. Легко подметить следующую закономерность: количество информации I, содержащееся в выбранном сообщении, определяется как двоичный логарифм n:
Слайд 16 Справедливо утверждение Хартли: если во множестве X={x1,x2,…,xn} выделить
произвольный элемент xi ∈ X , то, чтобы его
найти, необходимо получить не менее ld(n) единиц информации.Недостаток формулы Хартли заключается в том, что она не учитывает неравновероятность различных рассматриваемых состояний.
Слайд 19 Для неравновероятных процессов американский учёный Клод Шеннон предложил
(1948 г.) другую формулу определения количества информации, которая учитывает
возможную неодинаковую вероятность сообщений во множестве сообщений.Вероятность – это численная мера достоверности случайного события, которая при большом числе испытаний близка к отношению числа случаев m, когда событие осуществилось (положительных исходов), к общему числу случаев n:
Например, если много раз подбрасывать монетку, то она упадёт орлом вверх примерно в половине случаев. Это значит, что вероятность выпадения орла равна 0,5, или 50%.
Вероятность любого события – это число, принадлежащее отрезку [0;1]. Событие с вероятностью 0 называют невозможным, а с вероятностью 1 – достоверным.
Свойство вероятностей:
Слайд 20 Можно представить что для того, чтобы получить какой
то символ от источника сообщения нужно перебрать по крайней
мере (с вероятностью близкой к 1) n символов, где n=1/p. p –вероятность появления символа. Чтобы получить из этих символов необходимый нам, нужно сделать двоичный логарифм переборов ld(n).Если найти среднее значение количества таких переборов для всех символов получим формулу Шеннона:
бит
Эта величина получила название информационная энтропия, или энтропия источника сообщений.
мера Шеннона количества информации (формула Шеннона).
Энтропия характеризует информационную мощность данного множества (ансамбля) сообщений и является мерой неопределенности, которая имеется в этом множестве.
Слайд 21
Из формулы непосредственно вытекают свойства энтропии:
энтропия заранее известного
сообщения равна 0;
во всех других случаях H > 0.
Чем
больше энтропия системы, тем больше степень ее неопределенности. Поступающее сообщение полностью или частично снимает эту неопределенность. Поэтому количество информации можно измерять тем, насколько понизилась энтропия системы после поступления сообщения: Уменьшая энтропию, мы получаем информацию – в этом и заключается смысл научного познания!
Слайд 22
Кодирование источника сообщений
Как уже отмечалось, результат одного отдельного
альтернативного выбора может быть представлен как 0 или 1.
Тогда выбору всякого сообщения (события, символа т.п.) в массиве сообщений соответствует некоторая последовательность двоичных знаков 0 или 1, то есть двоичное слово. Это двоичное слово называют кодировкой, а множество кодировок источника сообщений – кодом источника сообщений.Слайд 23 Если количество символов представляет собой степень двойки (n
= 2N) и все знаки равновероятны Pi = (1/2)N,
то все двоичные слова имеют длину L=N=ld(n). Такие коды называют равномерными кодами.Более оптимальным с точки зрения объема передаваемой информации является неравномерное кодирование, когда разным сообщениям в массиве сообщений назначают кодировку разной длины. Причем, часто происходящим событиям желательно назначать кодировку меньшей длины и наоборот, т.е. учитывать их вероятность.
Слайд 24
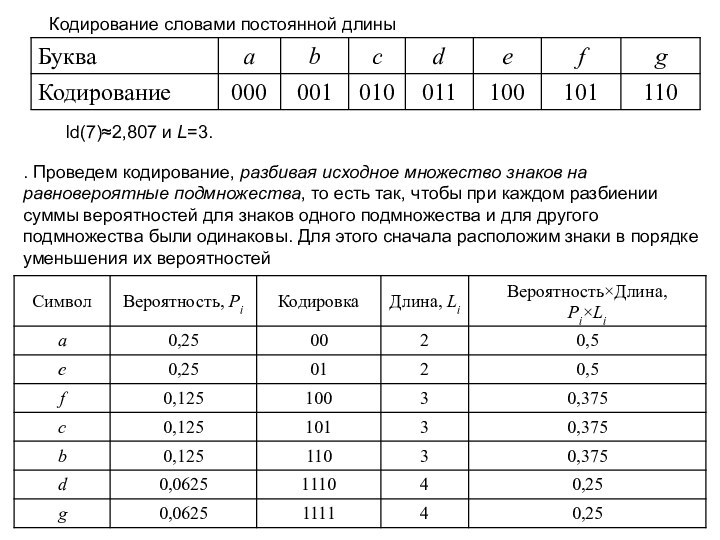
Кодирование словами постоянной длины
ld(7)≈2,807 и L=3.
. Проведем
кодирование, разбивая исходное множество знаков на равновероятные подмножества, то
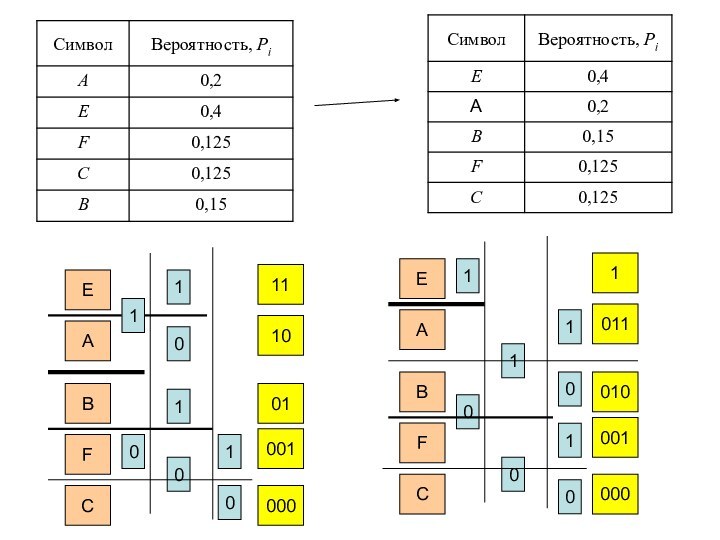
есть так, чтобы при каждом разбиении суммы вероятностей для знаков одного подмножества и для другого подмножества были одинаковы. Для этого сначала расположим знаки в порядке уменьшения их вероятностейСлайд 25 В общем случае алгоритм построения оптимального кода Шеннона-Фано
выглядит следующим образом:
1. сообщения, входящие в ансамбль, располагаются в
столбец по мере убывания вероятностей;2. выбирается основание кода K (в нашем случае К=2);
3. все сообщения ансамбля разбиваются на K групп с суммарными вероятностями внутри каждой группы как можно близкими друг к другу.
4. всем сообщениям первой группы в качестве первого символа присваивается 0, сообщениям второй группы – символ 1, а сообщениям K-й группы – символ (K–1); тем самым обеспечивается равная вероятность появления всех символов 0, 1,…, K на первой позиции в кодовых словах;
5. каждая из групп делится на K подгрупп с примерно равной суммарной вероятностью в каждой подгруппе. Всем сообщениям первых подгрупп в качестве второго символа присваивается 0, всем сообщениям вторых подгрупп – 1, а сообщениям K-х подгрупп – символ (K–1).
6. процесс продолжается до тех пор, пока в каждой подгруппе не окажется по одному сообщению.
Слайд 27 При неравномерном кодировании вводят среднюю длину кодировки, которая
определяется по формуле
В общем же случае связь между
средней длиной кодового слова L и энтропией H источника сообщений дает следующая теорема кодирования Шеннона:имеет место неравенство L ≥ H, причем L = H тогда, когда набор знаков можно разбить на точно равновероятные подмножества;
всякий источник сообщений можно закодировать так, что разность L – H будет как угодно мала.
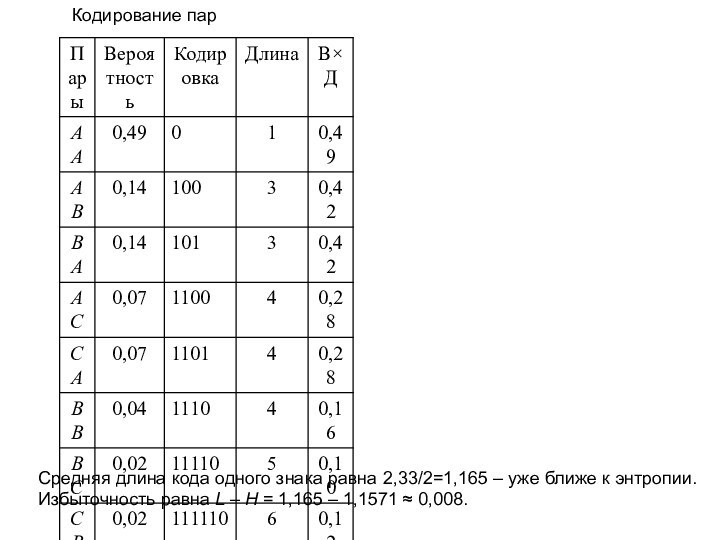
Разность L–H называют избыточностью кода (мера бесполезно совершаемых альтернативных выборов).
следует не просто кодировать каждый знак в отдельности, а рассматривать вместо этого двоичные кодирования для nk групп по k знаков. Тогда средняя длина кода i-го знака хi вычисляется так:
L = (средняя длина всех кодовых групп, содержащих хi)/k.
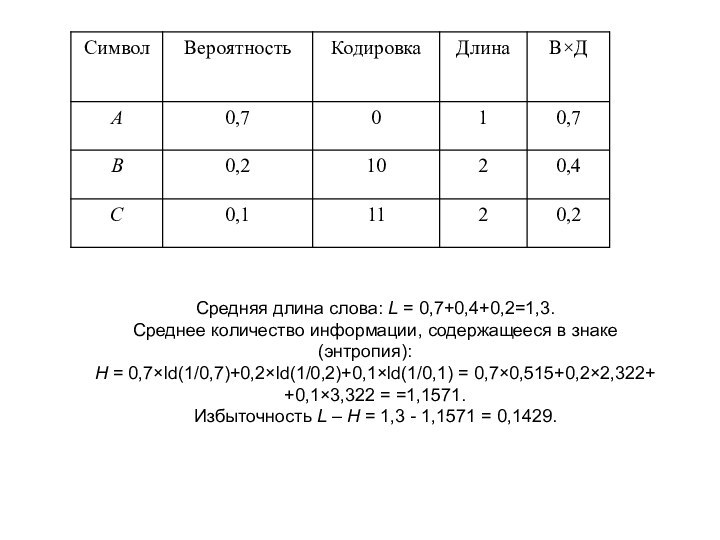
Слайд 28
Средняя длина слова: L = 0,7+0,4+0,2=1,3.
Среднее количество информации,
содержащееся в знаке (энтропия):
H = 0,7×ld(1/0,7)+0,2×ld(1/0,2)+0,1×ld(1/0,1) = 0,7×0,515+0,2×2,322+
+0,1×3,322
= =1,1571.Избыточность L – H = 1,3 - 1,1571 = 0,1429.