Презентация на тему Применение диаграмм Эйлера-Вена для решения задач математики и информатики

собрано огромное количество информации, разобраться в ней бывает непросто.

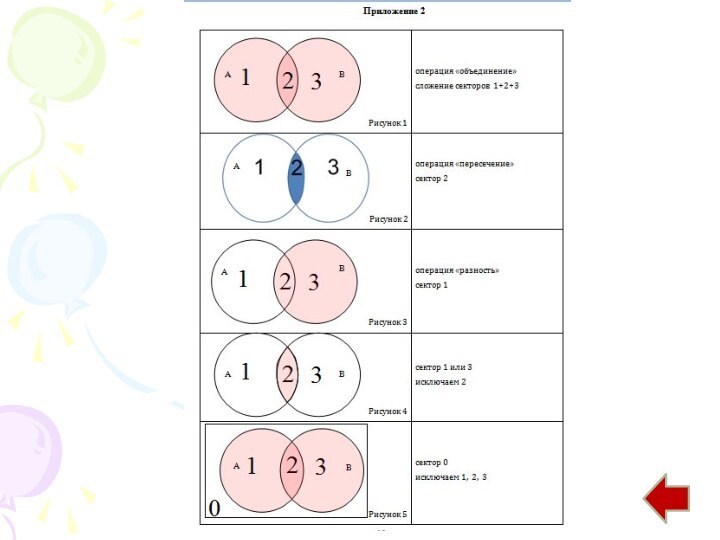
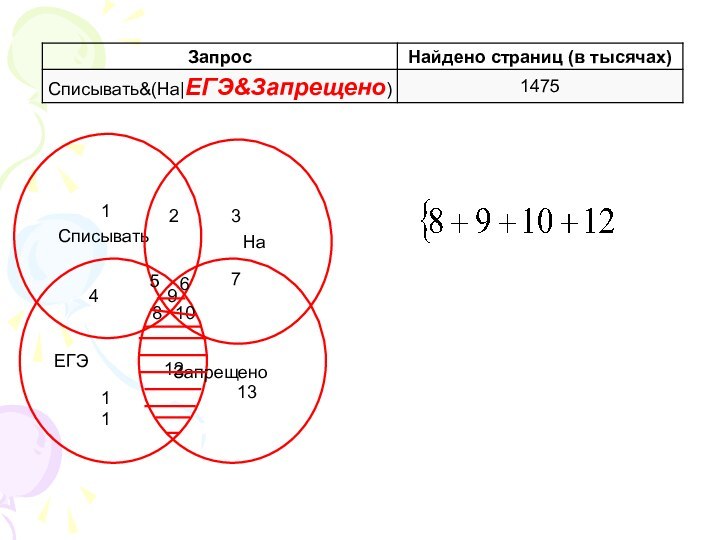
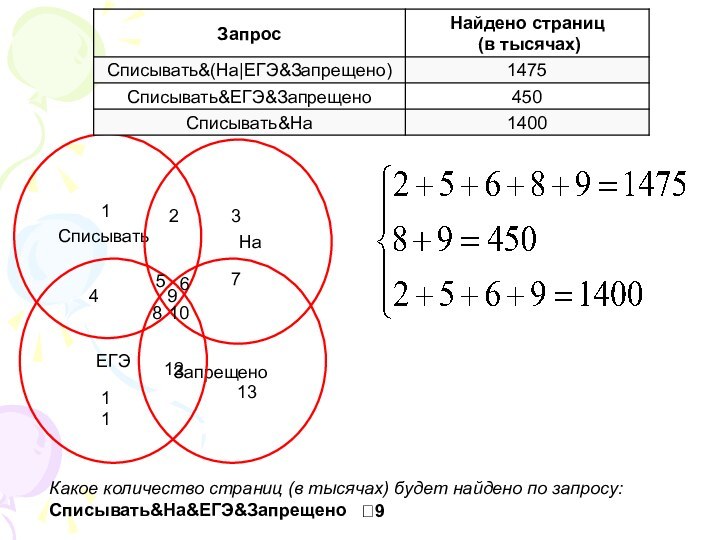
Находить логические связи между явлениями и понятиями помогают «Круги Эйлера» – это практичный и удобный метод решения логических задач.
«Круги Эйлера» находят широкое применение в повседневной жизни, в науке, ими стоит уметь пользоваться каждому.
Вышеуказанные причины определили актуальность и важность темы исследовательской работы.

с методом решения задач с использованием кругов Эйлера
Задачи:
Познакомиться с

литературой по теме: круги Эйлера;
Рассмотреть способы решения задач раздела математической логики в математике и информатике;
Показать наглядность и быстроту способа решения задач с использованием кругов Эйлера;
Сделать выводы о проделанной работе.
Гипотеза
Применение кругов Эйлера-Вена обеспечивает простоту, наглядность и быстроту решения задач раздела математической логики в математике и информатике.

тихой Швейцарии. Он принадлежит к числу гениев, чьё творчество

стало достоянием всего человечества.
В одной из 850 написанных работ Эйлером появились круги. Впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
Позднее работу с кругами продолжил учёный Джон Венн  и этот приём назвали «диаграммы Эйлера-Венна», который используется во многих областях: теория множеств, теория вероятностей, логики, статистики, компьютерных науках.

Приложение 1

графическая схема, с помощью которой можно изобразить отношения между

множествами для наглядного представления.
С множествами можно выполнять определенные операции. Операции над множествами рассматриваются для получения новых множеств из уже существующих. К основным операциям, которые можно выполнять над множествами, относятся следующие:
объединение;
пересечение;
разностью;
симметрическая разность;
абсолютным дополнение;

Приложение 2

существенно упрощают понимание сложных математических формулировок и наглядно отражают

суть определений.
Этот метод позволяет развивать математические представления и использовать их при изучении окружающего нас мира.
С помощью кругов Эйлера удобнее всего решать логические задачи на пересечение и объединение множеств.
Множеств может быть два, а может быть и больше. Чем больше множеств, тем труднее становится решить задачу.
С помощью кругов Эйлера на практике можно решать задачи логики, биологии, философии и других областей. Проиллюстрируем это на примерах.

Приложение 3

среди одноклассников. На первом этапе я предложил им решить

поставленную задачу и обозначил время 10 минут.
Задача 1.
В трех седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке – 10 ребят из хора, в хоре – 6 спортсменов, в драмкружке – 8 спортсменов; 3 спортсмена посещают и драмкружок, и хор.
Необходимо выяснить:
Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?
Сколько ребят занято только спортом?

Результат

к ребятам почему, я получил ответ – сложно, сначала

надо как-то это нарисовать схемой…

метод Эйлера-Венна по следующему алгоритму:
Изобразить кругами Эйлера заданное

по условию задачи количество множеств;
Пронумеровать все полученные сегменты;
Выразить сегментами дано из условия задачи;
Выразить сегментами неизвестное из условия задачи;
Используя полученные уравнения выполнить подстановки и найти результат

Эксперимент

них по русскому языку имеют «тройки» 19 человек, по

математике – 17 человек и по истории – 22 человека.
Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»?

Эксперимент

все полученное множество состоит из суммы сегментов 1,2,3,4,5,6,7.
По

русскому языку имеют «тройки» 19 человек. Сумма сегментов 1,2,4,5

По математике имеют «тройки» 17 человек. Сумма сегментов 2,3,5,6

По истории имеют «тройки» 22 человека. Сумма сегментов 4,5,6,7

Решение:

предметам. Сегмент 5
Только по одному предмету по русскому языку

имеют «тройки» 4 человека. Сегмент 1

Только по одному предмету по математике имеют «тройки» 4 человека. Сегмент 3

Только по одному предмету по истории имеют «тройки» 11 человек. Сегмент 7

Решение:

на поставленный вопрос - сколько человек учится без «троек»?

М=17

Р=19

И=22

4

4

11

Решение:

7

5

?

?

?

на поставленный вопрос - сколько человек учится без «троек»?

М=17

Р=19

И=22

4

4

11

5

2

6

4

4

4

11

5

2

6

4

36

40 – 36 = 4

Решение:

6

4

2

5

4

4

11

поставленную задачу и обозначил время.

Результат Приложение 4
Эксперимент

и нашли все ответы на поставленные вопросы. …

я предварительно изучив литературу по данному вопросу. Особое внимание

уделив приоритету выполнения операций показал ребятам возможность использования кругов Эйлера-Венна для решения задачи по информатике на запросы

Решение

Задача 3. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

обозначения логической операции «ИЛИ» используется символ «|», а для

обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Какое количество страниц (в тысячах) будет найдено по запросу:
Списывать&На&ЕГЭ&Запрещено

Списывать

На

ЕГЭ

Запрещено

На
ЕГЭ
Запрещено
2
3
4
5
6
7
8
9
10
11
12
13

На
ЕГЭ
Запрещено
2
3
4
5
6
7
8
9
10
11
12
13

На
ЕГЭ
Запрещено
2
3
4
5
6
7
8
9
10
11
12
13

На
2
3
4
5
6
7
8
9
10
11
12
13

(в тысячах) будет найдено по запросу:
Списывать&На&ЕГЭ&Запрещено

На

2

3

4

5

6

7

8

9

10

11

12

13

9

8=75
9?
2) 8+9=450
75+9=450
9=450-75
9=375

и интернет-источники по использованию кругов Эйлера-Венна; основные операции и

приоритет их выполнения; проиллюстрировано применение кругов Эйлера для решения различных задач; рассмотрены способы решения задач раздела математической логики; подробно рассмотрено применение кругов Эйлера-Вена для решения задач математики и информатики.

Результаты исследования

пришел к следующим выводам:
Чем сложнее и запутаннее логическая задача,

связанная с множествами, тем полезнее будет нарисовать диаграмму с кругами Эйлера. После этого решение значительно упрощается.
Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Знания по этой теме мне пригодятся при сдаче ОГЭ и ЕГЭ по математике и информатике и при написании олимпиадных работ по данным предметам.

За страницами учебника математики. Пособие для учащихся 5 –

6 кл./ И.Я Депман.  М.: Просвещение, 1999.
Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей/ Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993.
Игнатьев. Е.И.  В царстве смекалки, или Арифметика для всех: Книга для семьи и школы. Опыт математической хрестоматии в 3 книгах/Худож. Н.Я. Бойко. – Ростов н/Д: Кн. Изд-во, 1995.
Математика: 6 класс: Дидакт. материалы для общеобразова. учеб. заведений/Г.В.Дорофеев, С.Б.Суворова, И.Ф.Шарыгин и др.- М.: Дрофа, 1996.
Фарков, А.В. Математические олимпиады в школе.5–11 классы./   А.В. Фарков. М.: Айрис–пресс, 2007.
Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 2000. – 95 с.: ил.
Интернет-ресурсы:
http://www.tutoronline.ru/blog/krugi-jejlera;
http://logika.vobrazovanie.ru/index.php?link=kr_e.html;
http://mmmf.msu.ru/archive/20122013/z5/z5090313.html;