- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Растровая графика
Содержание
- 2. Алгоритмы растровой графикиРастеризация графических примитивов.Устранение лестничного эффекта.Заполнение областей.Растеризация сплошных многоугольников.Удаление невидимых линий
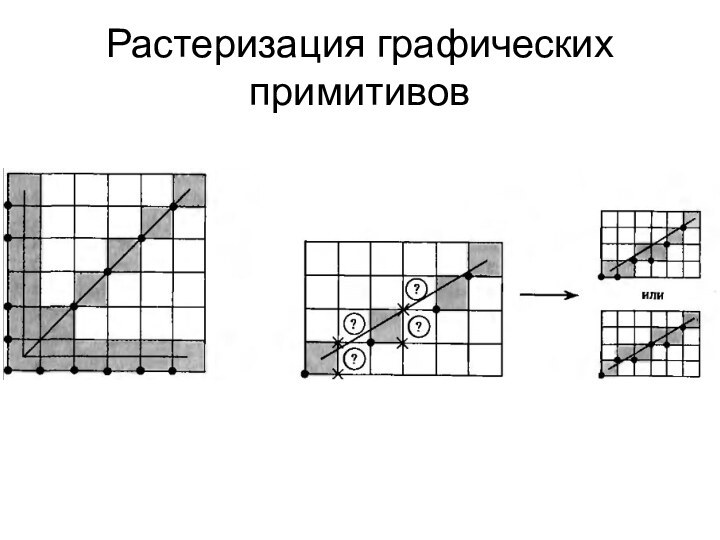
- 3. Растеризация графических примитивов
- 4. Растеризация отрезковПростейший алгоритмПошаговый алгоритмАлгоритм БрезенхемаАлгоритм ЦДА
- 5. Уравнение отрезка прямой(x1, y1), (x2, y2) –
- 6. Простейший алгоритмx = x1;y = y1;while (x
- 7. Пошаговый алгоритмx = x1;y = y1;while (x
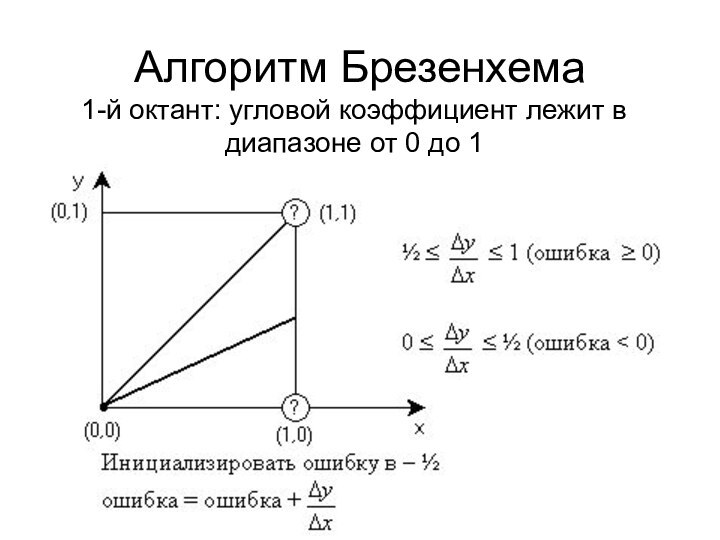
- 8. Алгоритм Брезенхема1-й октант: угловой коэффициент лежит в диапазоне от 0 до 1
- 9. Алгоритм Брезенхема
- 10. Целочисленный алгоритм Брезенхема (1-й октант)x = x1;
- 11. Общий алгоритм Брезенхемаx = x1; y =
- 12. Алгоритм ЦДАL = Max(|x2 – x1|, |y2
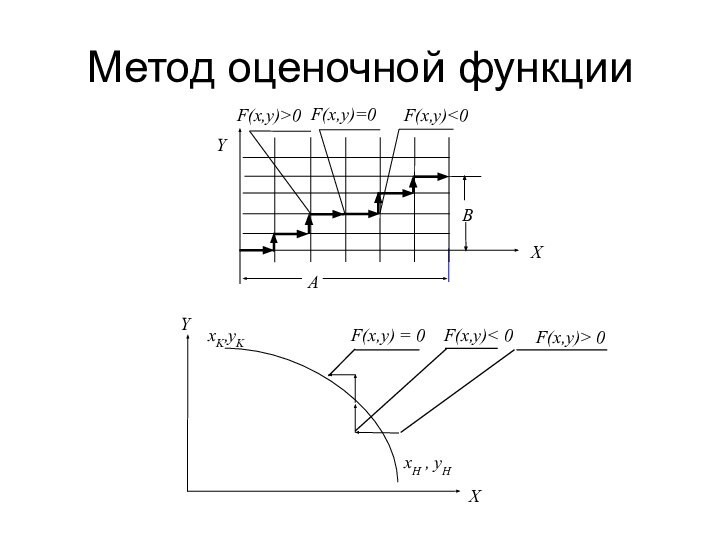
- 13. Методы растеризации графических примитивовМетод оценочной функцииМетод цифровых дифференциальных анализаторов
- 14. Метод оценочной функции
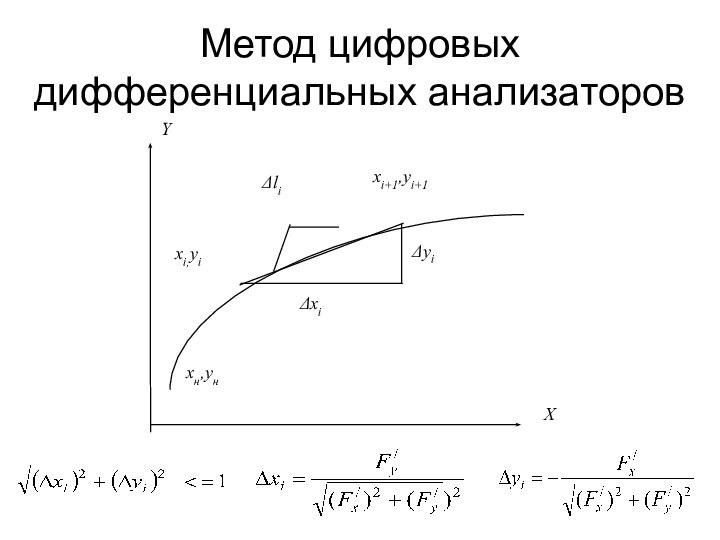
- 15. Метод цифровых дифференциальных анализаторов
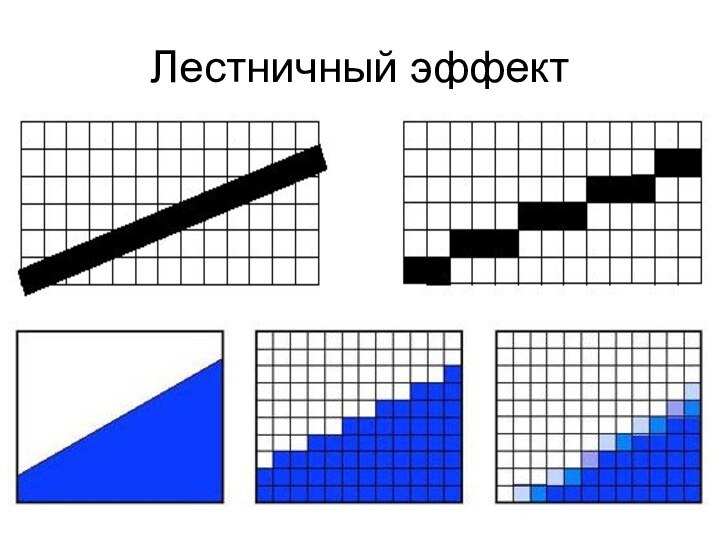
- 16. Лестничный эффект
- 17. Устранение лестничного эффектаВыравнивание – каждый пиксел высвечивается
- 18. Алгоритм ВуПри рисовании линий обычным образом с
- 19. Алгоритм Ву
- 20. Алгоритм Ву
- 21. Целочисленный алгоритм Ву// Координаты концов отрезка -
- 22. Заполнение областейПострочное сканированиеЗаполнение с затравкой
- 23. Построчное сканированиеИмеется область, граница которой разложена в
- 24. Заполнение с затравкойУказать затравочный пиксел внутри контура.Поместить
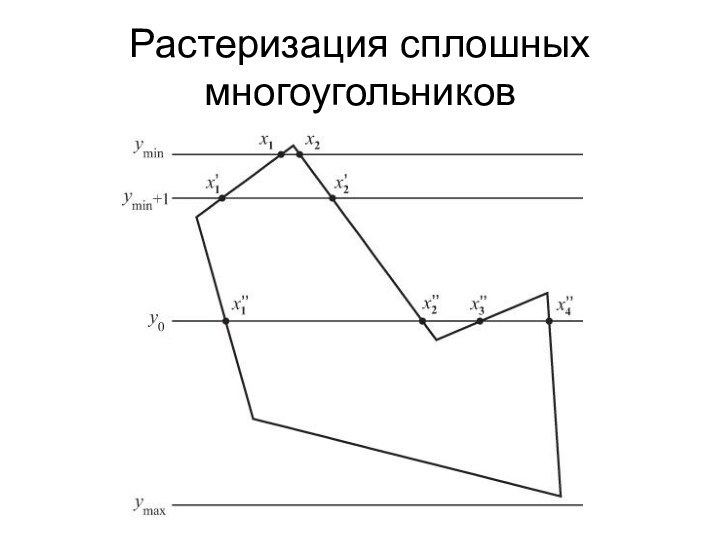
- 25. Растеризация сплошных многоугольниковРастеризация всех негоризонтальных ребер многоугольника.Все
- 26. Растеризация сплошных многоугольников
- 27. Удаление невидимых линийАлгоритмы, работающие в объектном пространстве.Алгоритмы, работающие в пространстве изображения.
- 28. Скачать презентацию
- 29. Похожие презентации
Алгоритмы растровой графикиРастеризация графических примитивов.Устранение лестничного эффекта.Заполнение областей.Растеризация сплошных многоугольников.Удаление невидимых линий





















Слайд 2
Алгоритмы растровой графики
Растеризация графических примитивов.
Устранение лестничного эффекта.
Заполнение областей.
Растеризация
сплошных многоугольников.
Слайд 5
Уравнение отрезка прямой
(x1, y1), (x2, y2) – целочисленные
координаты начальной и конечной точек отрезка.
y = ax +
b – уравнение отрезка прямой.y1 = ax1 + b
y2 = ax2 + b
a = (y2 – y1) / (x2 – x1)
b = (y1x2 – x1y2) / (x2 – x1)
Слайд 6
Простейший алгоритм
x = x1;
y = y1;
while (x ≤
x2)
{
PutPixel(x, y);
x = x + 1;
y = Round(ax +
b);}
Слайд 7
Пошаговый алгоритм
x = x1;
y = y1;
while (x ≤
x2)
{
PutPixel(x, y);
x = x + 1;
y = Round(y +
a);}
Слайд 9 Алгоритм Брезенхема
(1-й октант)
x = x1;
y = y1; Δx = x2 – x1; Δy = y2 – y1; e = Δy / Δx – 0.5;for (i = 1; i ≤ Δx; i = i + 1)
{
PutPixel(x, y);
while (e ≥ 0)
{
y = y + 1;
e = e – 1;
}
x = x + 1;
e = e + Δy / Δx;
}
Слайд 10
Целочисленный алгоритм Брезенхема (1-й октант)
x = x1; y
= y1; Δx = x2 – x1; Δy =
y2 – y1; e = 2 * Δy – Δx;for (i = 1; i ≤ Δx; i = i + 1)
{
PutPixel(x, y);
while (e ≥ 0)
{
y = y + 1;
e = e – 2 * Δx;
}
x = x + 1;
e = e + 2 * Δy;
}
Слайд 11
Общий алгоритм Брезенхема
x = x1; y = y1;
Δx = |x2 – x1|; Δy = |y2 –
y1|;s1 = Sign(x2 – x1); s2 = Sign(y2 – y1);
d = 0;
if (Δy > Δx) { Swap(Δx, Δy); d = 1; }
e = 2 * Δy – Δx;
for (i = 1; i ≤ Δx; i = i + 1)
{ PutPixel(x, y);
while (e ≥ 0)
{ if (d = 1) x = x + s1; else y = y + s2;
e = e – 2 * Δx;
}
if (d = 1) y = y + s2; else x = x + s1;
e = e + 2 * Δy;
}
Слайд 12
Алгоритм ЦДА
L = Max(|x2 – x1|, |y2 –
y1|);
Δx = (x2 – x1) / L; Δy =
(y2 – y1) / L; x = x1 + 0.5 * Sign(Δx);
y = y1 + 0.5 * Sign(Δy);
for (i = 1; i ≤ L; i = i + 1)
{
PutPixel(Round(x), Round(y));
x = x + Δx;
y = y + Δy;
}
Слайд 13
Методы растеризации графических примитивов
Метод оценочной функции
Метод цифровых дифференциальных
анализаторов
Слайд 17
Устранение лестничного эффекта
Выравнивание – каждый пиксел высвечивается с
яркостью, пропорциональной площади пиксела, которую занимает отрезок.
Изменение разрешения –
подготовка изображения высокого разрешения (кратного реальному) с последующим масштабированием и использованием сглаживающего фильтра.Учет наклона отрезка – изменение яркости в зависимости от наклона отрезка (максимум у вертикального отрезка – 1, минимум у горизонтального отрезка – 0.707).
Слайд 18
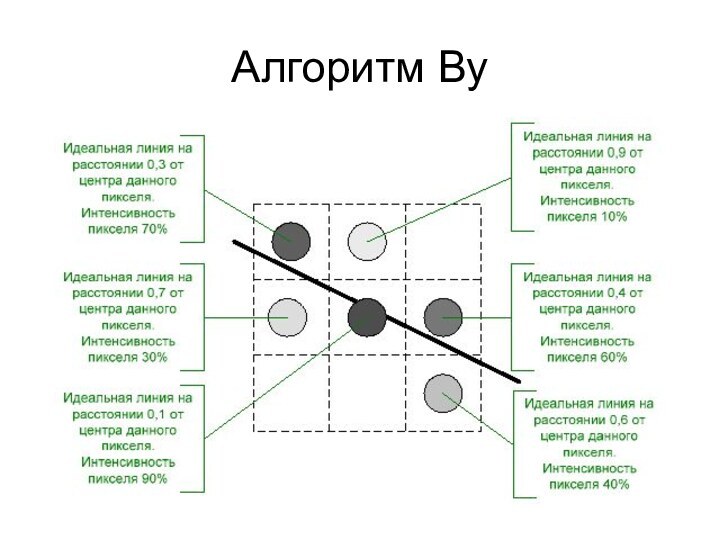
Алгоритм Ву
При рисовании линий обычным образом с каждым
шагом по основной оси высвечиваются два пиксела по неосновной
оси.Их интенсивность подбирается пропорционально расстоянию от центра пиксела до идеальной линии – чем дальше пиксел, тем меньше его интенсивность. Значения интенсивности двух пикселов дают в сумме 100 %, т.е. интенсивность одного пиксела, точно попавшего на идеальную линию.
Горизонтальные, вертикальные и диагональные линии не сглаживаются.
Т.о. учитываются особенности человеческой зрительной системы.
Слайд 21
Целочисленный алгоритм Ву
// Координаты концов отрезка - (0,
0) и (a, b), a > 0, b >
0, b < a// plot(x,y,I) закрашивает пиксель (x, y) с интенсивностью I
// I0 - максимальная интенсивность (2 ^ m - 1)
x0 = 0; x1 = a; y0 = 0; y1 = b;
plot(x0,y0,I0); plot(x1,y1,I0);
D = 0;
d = floor( (b / a) * 2 ^ n + 0.5 ); // меньшее целое
while ( x0 < x1 )
{ D = D + d;
if( произошло переполнение D ) { y0++; y1--; }
I1 = D / 2 ^ (n - m); // битовый сдвиг вправо на n - m
I2 = двоичное_дополнение( I1 );
plot(x0, y0, I1); plot(x0, y0+1, I2);
plot(x1, y1, I1); plot(x1, y1-1, I2);
x0++; x1--;
}
Слайд 23
Построчное сканирование
Имеется область, граница которой разложена в растр.
Внутри
задана точка.
Заданы значения: a – граничных пикселов, b –
внутренних пикселов до заполнения, c – внутренних пикселов после заполнения.Объект заключается в прямоугольную оболочку.
Проводится построчное сканирование прямоугольной оболочки: в строке находится пиксел со значением a, затем пиксел, следующий за ним и имеющий значение b, которое меняется на c, и так до тех пор, пока не будет встречен еще один пиксел со значением a, после чего осуществляется переход на следующую строку.
Слайд 24
Заполнение с затравкой
Указать затравочный пиксел внутри контура.
Поместить затравочный
пиксел в стек.
Пока стек не пуст:
извлечь пиксел из стека;
присвоить
пикселу требуемое значение;для каждого из соседних четырехсвязных пикселов проверить:
Является ли он граничным;
Не присвоено ли ему требуемое значение;
проигнорировать пиксел в любом из этих двух случаев, иначе поместить пиксел в стек.